Смешанное произведение трех векторов и его свойства

Смешанным произведением трёх векторов  называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор  умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .

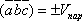Таким образом,  и .

Доказательство. Отложим векторы  от общего начала и построим на них параллелепипед. Обозначим  и заметим, что . По определению скалярного произведения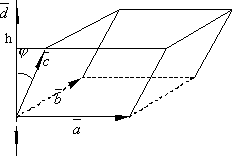

. Предполагая, что  и обозначив через h высоту параллелепипеда, находим .

Таким образом, при 

Если же , то  и . Следовательно, .

Объединяя оба эти случая, получаем  или .

Из доказательства этого свойства в частности следует, что если тройка векторов  правая, то смешанное произведение , а если  – левая, то .

2. Для любых векторов 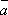, , 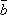 справедливо равенство

.

Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что  и . Причём знаки "+" и "–" берутся одновременно, т.к. углы между векторами  и  и  и  одновременно острые или тупые.

3. При перестановке любых двух сомножителей смешанное произведение меняет знак.

Действительно, если рассмотрим смешанное произведение , то, например,  или

.

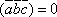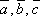4. Смешанное произведение  тогда и только тогда, когда один из сомножителей равен нулю или векторы  – компланарны.

Доказательство.

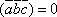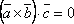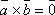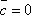1. Предположим, что , т.е. , тогда  или  или .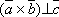

Если , то  или  или . Поэтому  – компланарны.

Если , то , ,  - компланарны.

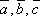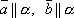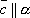2. Пусть векторы  – компланарны и α – плоскость, которой они параллельны , т. е.  и . Тогда 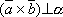, а значит 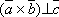, поэтому 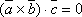 или .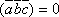

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора образуют базис в пространстве, если .

Если векторы заданы в координатной форме , то можно показать, что их смешанное произведение находится по формуле:

.

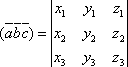Т. о., смешанное произведение равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

Примеры.

3. Показать, что векторы 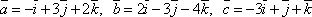 образуют базис в пространстве.

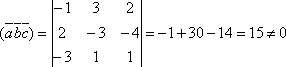, т.е. векторы  – базис.

4. Найти объём пирамиды с вершинами в точках A(2; -2; 0), B(-1; 4; -4), C(4; -8; 5), D(1; -7; 0). Правую или левую тройку образуют векторы  и ?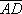

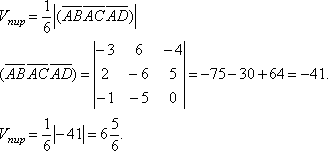
Т. к. , то тройка векторов левая.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Уравнение F(x, y, z) = 0 определяет в пространстве Oxyz некоторую поверхность, т.е. геометрическое место точек, координаты которых x, y, z удовлетворяют этому уравнению. Это уравнение называется уравнением поверхности, а x, y, z – текущими координатами.

Однако, часто поверхность задаётся не уравнением, а как множество точек пространства, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из её геометрических свойств.

ПЛОСКОСТЬ.

НОРМАЛЬНЫЙ ВЕКТОР ПЛОСКОСТИ.

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ

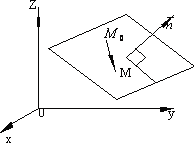
Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора , перпендикулярного этой плоскости, и некоторой фиксированной точки M₀(x₀, y₀,z₀), лежащей в плоскости σ.

Вектор  перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор  имеет координаты .

Выведем уравнение плоскости σ, проходящей через данную точку M₀ и имеющей нормальный вектор . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор .

Для любой точки MΠσ вектор .Поэтому их скалярное произведение равно нулю . Это равенство – условие того, что точка MΠσ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через  радиус-вектор точки M,  – радиус-вектор точкиM₀, то  и уравнение можно записать в виде

.

Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как , то

.

Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z.

Примеры.

1. Составить уравнение плоскости, проходящей через точку М(1;-2;3) перпендикулярно вектору .

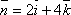Используя выведенное уравнение, получим 2(x-1)+0(y+2)+4(z-3)=0 или x+2z-7=0.

2. Составить уравнение плоскости, проходящей через точки A(1;2;3), B(-1;0;0), C(3;0;1).

Чтобы составить требуемое уравнение, нужно найти вектор перпендикулярный плоскости. Заметим, что таким вектором будет вектор . Найдем это вектор. . Тогда

.

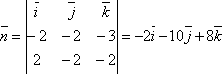Взяв в качестве точки, через которую проходит плоскость точку A, получим уравнение –2(x-1)-10(y-2)+8(z-3)=0 или x+5y-4z+1=0.

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ

Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости. Это уравнение записывается в виде:

Ax+By+Cz+D=0

и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.

Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.

Свободный член равен нулю D= 0. В этом случае уравнение плоскости принимает видAx+Cy+Bz=0. Т.к. числа x=0, y=0, z=0 удовлетворяют уравнению плоскости, то она проходит через начало координат. Один из коэффициентов при текущих координатах равен нулю. Пусть например A =0. В этом случае уравнение плоскости имеет вид By+Cz+D=0. Нормальный вектор плоскости имеет координаты  и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox. Аналогично, если B= 0, то плоскость параллельна оси Oy и C= 0 – плоскость параллельна оси Oz. Т.о., если в уравнении плоскости один из коэффициентов при текущей координате равен нулю, то плоскость параллельна соответствующей координатной оси. Коэффициент при текущей координате и свободный член равны нулю. Например, A = D = 0. В этом случае уравнению By + Cz = 0 соответствует плоскость, проходящая через начало координат (согласно п.1). Кроме того, учитывая п.2, данная плоскость должна быть параллельна оси Ox. Следовательно, плоскость проходит через ось Ox. Аналогично, при B=D=0 плоскость Ax+Cz=0 проходит через ось Oy. При C=D=0 плоскость проходит через ось Oz. Два коэффициента при текущих координатах раны нулю. Пусть, например, A=B=0. Тогда плоскость Cz+D=0 в силу п.2 будет параллельна осям Oxи Oy, а следовательно параллельна координатной плоскости xOy, и проходит через точку с координатой . Аналогично, уравнениям Ax+D=0 и By+D=0 соответствуют плоскости, параллельные координатным плоскостям yOzи xOz. Два коэффициента при текущих координатах и свободный член равны нулю. Пусть, например, A=B=D=0. Тогда уравнение плоскости имеет вид Cz=0 или z=0. Эта плоскость проходит через начало координат и параллельна осям Ox и Oy, т. е. уравнение определяет координатнуюплоскость xOy. Аналогично, x=0 – уравнение координатной плоскости yOz и y=0 – плоскость xOz.

Примеры.

1. Составить уравнение плоскости, проходящей параллельно оси Oy, через точки M₁(1; 0; -1), M₂(-1; 2;0).

Так как ось Oy параллельна , то уравнение плоскости Ax+Cy+D=0. Учитывая, что M₁Πα, M₂Πα, подставим координаты этих точек в уравнение и получим систему из двух линейных уравнений с тремя неизвестными

Положив D= 1, найдем A= 1 и C= 2. Следовательно, уравнение плоскости имеет видx+2z+1=0.

2. Составить уравнение плоскости, проходящей через точку M(2;3;-4) параллельно плоскости yOz (перпендикулярно оси Ox).

Так как yOz||α, то уравнениеплоскости будет Ax+D=0. С другой стороны MΠα, поэтому 2A+D=0, D=-2A. Поэтому плоскость имеет уравнениеx-2=0.