8. Поиск области экстремума функции методом крутого восхождения (спуска)

8.1. Цель и задачи

Цель – изучить методику планирования многофакторного эксперимента для поиска области расположения экстремума функции.

Задачи – освоить основные понятия планирования многофакторного эксперимента по методу крутого спуска (восхождения), научиться планировать, проводить и обрабатывать результаты многофакторного эксперимента при поиске опытным путем экстремума функции.

2. Задание

Для уровней варьирования 3-х факторов, принятые в задании 6, и уравнения регрессии (6.6) :

- рассчитать допустимые смещения вдоль осей для движения вдоль вектора градиента и составить план эксперимента;

- с помощью имитационной модели для условного 3-х факторного пространства проводить опыты, начиная с центра факторного пространства;

- после каждого опыта провести анализ динамики изменения частного сечения неизвестной функции отклика и проводить опыты до достижения максимума.

2. Порядок выполнения задания

1. Задаемся уровнями варьирования факторов Таблица 8.1). При выполнении задания уровни варьирования перенесем из задания 6.

Таблица 8.1.

Уровни варьирования действующих факторов

Уровни	X1	X2	X3
1.Нижний
2.Верхний
3.Основной
4. Интервал варьирования

2. В качестве опорного решения берем результаты полного факторного эксперимента (задание 6). Уравнение регрессии, полученное при проведении полного факторного эксперимента

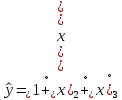. (8.1)

3. Построение расчетной таблицы и матрицы планирования (таблица 8.2).

3.1.В первую строчку запишем коэффициенты уравнения с соблюдением знака (учитываем только значимые значения коэффициентов).

3.2.Значения коэффициентов умножаем на величину интервала варьирования (табл.8.1) и результат записываем во вторую строчку.

3.3.Находим базовый коэффициент, соответствующий минимуму абсолютных значений второй строчки.

_3.4.Подсчитываем масштабный коэффициент и рассчитываем расчетный шаг движения вдоль градиента (строчка 3). Расчетные значения округляют до удобного для реализации эксперимента значения _Δi.

Таблица 8.2

_{Расчетная таблица матрица планирования эксперимента}

Показатель				Расчеты
Коэффициенты уравнения, ai				Min{| ai •Ji |}=_____ aбаз=______. Масштабный коэффициент: km=1/aбаз=______
2.Произведение ai •Ji
3.Расчетное смещение (шаг движения), ai ٠Ji٠km
4. Округленный шаг смещения Δi
0 (xio)				y0 =_______
1				y1 =_______
2				y2 =_______
3				y3 =_______

4. Проведение имитационного моделирования.

Задать начальную точку, соответствующую центру эксперимента (точка x_io ). Проведение эксперимента осуществляется в том же порядке, что и задании 6.

Результаты моделирования среднее [mean(y)] заносят в таблицу 8.2. и анализируем значения функции отклика. Если происходит увеличение функции, продолжаем движение вдоль градиента пока значения не начнут уменьшаться. В окрестности максимальной точки далее следует искать искомый максимум.

Контрольные вопросы:

1. Как выбрать начальную точку планирования эксперимента?

2. Как определить направление движения в факторном пространстве?

3. Как определить шаг движения вдоль градиента?

4. При каком условии прекращается проведение эксперимента?