7.1. Цель и задачи

Цель – изучить методику планирования дробного многофакторного эксперимента для получения линейной формы уравнения.

Задачи – освоить основные понятия планирования дробного многофакторного эксперимента, научиться планировать, проводить и обрабатывать результаты многофакторного эксперимента и оценивать адекватность уравнения.

2. Основные понятия и определения

Многофакторные процессы описываются зависимостью случайной величины у (показатель, отклик) от переменных (аргументов, действующих факторов) х_j (j = 1, 2,..., k) случайных величин, оцениваемых средними значениями, независимо от истинного закона распределения x_j.

, (7.1)

где ,- коэффициенты уравнения регрессии.

Проведение эксперимента предполагает одновременное изменение всех действующих факторов в соответствии с блоком планирования План-матрицы эксперимента (Таблица 7.2).

Для повышения точности оценочных значений коэффициентов уравнения регрессии (7.1) проводят параллельные (воспроизводимые) опыты (повторности).

2. Задание

С помощью имитационной модели для условного 3-х факторного пространства и диапазонов варьирования факторов, принятых при моделировании полного факторного эксперимента (задание 6):

- построить план-матрицу дробного факторного эксперимента ДФЭ 2^3-1;

- провести имитационное моделирование в соответствии с блоком планирования План-матрицы и заданными уровнями варьирования;

- провести дисперсионный анализ полученных результатов;

- получить уравнение регрессии и оценить его адекватность.

2. Порядок выполнения задания

1. Задаемся уровнями варьирования действующих факторов (таблица 7.1). В данном задании уровни варьирования факторов возьмем из задания 6.

Таблица 7.1.

Уровни варьирования действующих факторов

Уровни	X1	X2	X3
1.Нижний, xн	7	13	24
2.Верхний, xв	33	37	48
3.Основной, xо	20	25	36
4.Интервал варьирования, Ji	13	12	12

2. Составим План-матрицу (таблица 7.2) дробного факторного эксперимента 2^3-1. Для этого берем за основу План-матрицу ПФЭ 2² и приравниваем . Это означает, чтоa₃ будет учитывать одновременное влияние фактора x₃ и двух смешанных эффектов. Соответственно и коэффициенты a₁ и a₂ будут учитывать влияние на функцию отклика факторов и смешанные парные эффекты

Таблица 7.2

План-матрица ДФЭ 2^3-1

№ опыта				=
1	+	+	+	+	8,172	0,045	8,172
2	+	−	+	−	8,55	0,085	8,55
3	+	+	−	−	8,577	0,005	8,577
4	+	−	−	+	8,322	0.068	8,322

3. Проведем имитационное моделирование.

Проведение эксперимента осуществляется в том же порядке, что и в предыдущем задании 6.

Результаты моделирования заносят в таблицу 7.2 :

- среднее [mean(y)] ;

- дисперсию [var(y)].

4. Дисперсионный анализ результатов эксперимента

1. Проверка однородности ряда дисперсий

(7.2)

Критическое значения критерия Кохрена находим по таблице 8 (приложения1). Для N=4 , k=n-1=3-1=2 равно

. (7.3)

Расчетное значение критерия Кохрена сравниваем с критическим и делаем вывод: так, как <, то принимаем гипотезу о том, что ряд дисперсий однороден, и следовательно в серии опытов грубых ошибок нет.

2. Определяем дисперсию воспроизводимости

(7.4)

Число степеней свободы для дисперсии воспроизводимости равно.

3. Определяем коэффициенты уравнения регрессии (6.6) по методу наименьших квадратов

(7.4)

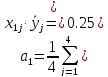-0,123)= - 0,031;

.

.

Получим уравнение .

4. Определяем дисперсию адекватности

(7.5)

Число степеней свободы равно Если дисперсия адекватности близка к 0, точки принадлежат поверхности и п 4.5 не проводят, считаем модель адекватной.

5. Для оценки адекватности полученного уравнения подсчитываем расчетное значение критерия Фишера

=----------=_________________. (7.6)

Критическое значение критерия находим по таблице (приложения 1) для α=0.05;

. (7.9)

Сравниваем расчетное значение с критическим, если дисперсия адекватности имее численной значение.

Контрольные вопросы:

1. По какому принципу формируется блок планирования?

2. Что оцениваю коэффициенты уравнения?

3. Можно ли по значение коэффициентов однозначно утверждать о силе влияния того или иного фактора ?

4. Какое преимущество и недостатки имеет метод дробного планирования?

5. Что означает ДФЭ _2n-k?