4. Проверка случайности выборки

Проверку гипотезы о случайности выборки проведем на основе метода разностей. Сформируем новую случайную величину как разницу между предшествующим и последующим значением (в порядке получения)

3.1 Сформулируем гипотезу:

H₀: выборка случайна;

H₁: выборка неслучайна.

3.2. В качестве критерия возьмем отношение двух характеристик рассеивания

, (1.8)

где – характеристика рассеивания случайной величины, подсчитанное по методу разностей.

. (1.9)

Расчетное значение критерия получим

. (1.10)

3.3. Критическое значение выбранного критерия для объема выборки n ≤ 20 находим по таблице 2 (приложения).

Для выборки объемом больше n>20 τ распределено по нормальному закону распределения с параметрами

; . (1.11)

В этом случае определяется из условия

. (1.12)

Для n=25, α=0,05 находим параметр нормирования ЗНР по таблице 10 (приложения1) соответствующий уровню доверительной вероятности 0,95, получим, для 0,05

Искомое значение будет равно 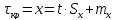. Значениеподсчитываем по формуле (1.11). Тогда

(1.13)

3.4. Вывод: так как , то выборка случайна.

5. Проверка достаточности выборки

4.1.Рассчитаем значения оценочное значение среднего (1) для первых 3, 5, 10 и 25 значений и построим график зависимости среднего от объема выборки

Объем выборки	3	5	10	25
	13,85	16,22	17,24	17,19

n

Рис. 1.2 Зависимость среднего от объема выборки n

Из графика видно, что среднее зависит от анализируемой величины и от объема выборки. Для достаточной выборки должно выполняться условие

, (1.14)

где I_дов – доверительный интервал для нахождения среднего значения; m_x – математическое ожидание среднего значения; α – доверительная вероятность ( в расчетах принимаем α=0,95).

Для соблюдения условия (1.14) должно выполняться условие

, (1.15)

где Δ – относительная погрешность определения среднего; - коэффициент Стьюдента (таблица , приложения 1),

Значение относительной погрешности задается методикой испытаний или измерений (в расчетах принимаем Δ=10% или 0,1).

4.2. Минимально необходимый объем подсчитываем из условия равенства (1.15)

. (1.16)

Полученное расчетное значение округляем до большего целого значения n_p =65.

Сравниваем полученное значение минимально необходимого числа опытов с объемом выборки и делаем вывод о достаточности имеющейся выборки. В нашем примере n_p =65 >N=25, следовательно выборка не достаточная по объему. В этом случае, необходимо провести дополнительную серию опытов.

3. Определение минимально необходимого числа измерений при разработке методики исследования.

В практической работе исследователя чаще всего встречается задача обоснования необходимого числа измерений при разработке рабочей методики испытаний. На этом этапе выборочных значений не имеем. Значения величин по формуле (1.16) найти не можем, так как каждое из них зависит от искомого объема выборки.

При выполнении задания необходимо самостоятельно разобраться и объяснить, как поступить в этом случае?

Контрольные вопросы:

1. Дать определение случайной величины и привести примеры из своей практики.

2. Как будут изменяться статистические характеристики случайной величины при увеличении и выборки?

3. Объяснить порядок проверки статистических гипотез.

4. Объяснить понятие статистического критерия.

5. Как сравнить два исследуемых идентичных процесса с разными средними и дисперсиями одного признака?