Вопросы для подготовки к экзамену по линейной алгебре (эк_без)

Вопросы для подготовки к экзамену по линейной алгебре и аналитической геометрии

Элементы линейной алгебры

1. Матрицы, виды матриц (квадратная, диагональная, единичная, нулевая).

2. Действия с матрицами (сложение, умножение на число, умножение матриц), их свойства; перестановочные матрицы, необходимое условие перестановочности матриц.

3. Определитель матрицы n–го порядка, свойства определителей.

4. Миноры и алгебраические дополнения. Разложение определителя по элементам произвольной строки или столбца.

5. Ранг матрицы. Ступенчатая матрица. Элементарные преобразования строк (столбцов) матрицы, определение. Теорема о ранге ступенчатой матрицы.

6. Обратная матрица, теорема о единственности обратной матрицы в случае ее существования. Способы нахождения обратной матрицы: с помощью элементарных преобразований, алгебраических дополнений.

7. Системы линейных уравнений, основная и расширенная матрицы системы, матричная форма записи системы линейных уравнений.

8. Системы линейных уравнений и методы их решения: с помощью обратной матрицы (обоснование), метод Крамера (обоснование), метод Гаусса (описание алгоритма).

Элементы векторной алгебры и аналитической геометрии

1. Вектор. Операции с векторами (сложение, умножение на число, скалярное произведение). Свойства скалярного произведения векторов. Коллинеарные векторы, определение. Необходимое и достаточное условия коллинеарности двух векторов.

2. Теорема о разложении вектора по двум неколлинеарным векторам.

3. Координаты вектора. Необходимое и достаточное условие коллинеарности двух векторов в координатной форме.

4. Скалярное произведение двух векторов, заданных координатами. Необходимое и достаточное условие перпендикулярности двух векторов, заданных координатами.

5. Линейная зависимость и линейная независимость векторов, определение. Основные теоремы о линейной зависимости: линейная зависимость системы векторов, содержащей нулевой вектор; содержащей два пропорциональных вектора. Связь между линейной зависимостью и коллинеарностью двух векторов. Связь между линейной зависимостью и компланарностью трех векторов.

6. Деление отрезка в данном отношении.

7. Уравнение линии на плоскости. Вывод уравнения окружности.

8. Уравнение прямой линии на плоскости. Направляющий и нормальный векторы прямой, определения. Уравнение прямой, заданной: точкой и направляющим вектором; точкой и нормальным вектором; точкой и угловым коэффициентом; двумя точками.

9. Взаимное расположение прямых на плоскости: угол между двумя прямыми; необходимые и достаточные условия параллельности и перпендикулярности двух прямых.

10. Общее уравнение прямой. Теорема о том, что любое уравнение первой степени относительно переменных x, y определяет прямую линию на плоскости.

11. Расстояние от точки до прямой.

12. Геометрический смысл линейных неравенств с двумя переменными.

13. Кривые второго порядка: эллипс (вывод канонического уравнения эллипса), гипербола (вывод канонического уравнения гиперболы), парабола (вывод канонического уравнения параболы).

14. Уравнение плоскости, заданной: точкой и нормальным вектором; тремя точками. Условия параллельности и перпендикулярности плоскостей. Угол между двумя плоскостями. Расстояние от точки до плоскости. Уравнение плоскости, проходящей через заданную точку параллельно заданной плоскости.

15. Уравнение прямой, заданной точкой и направляющим вектором; параметрические уравнения прямой. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.

16. Уравнение прямой, проходящей через заданную точку перпендикулярно заданной плоскости. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой.

Задания для подготовки к экзамену по линейной алгебре и аналитической геометрии

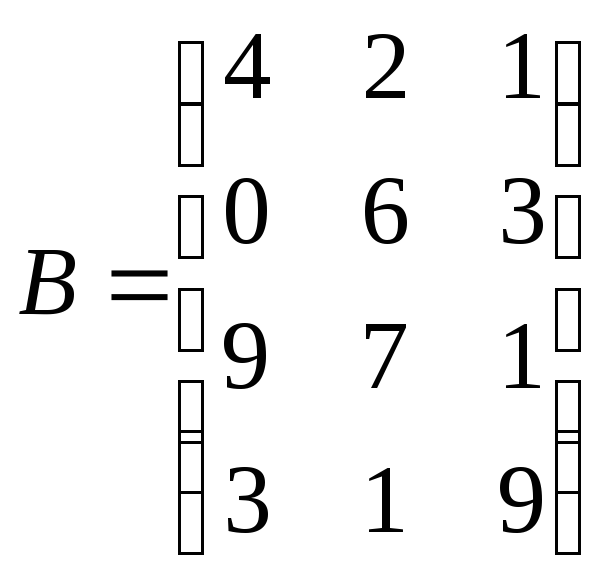1. Даны матрицы и . Найдите сумму этих матриц и разность А – В.

2. Найдите произведение матриц: а) б)

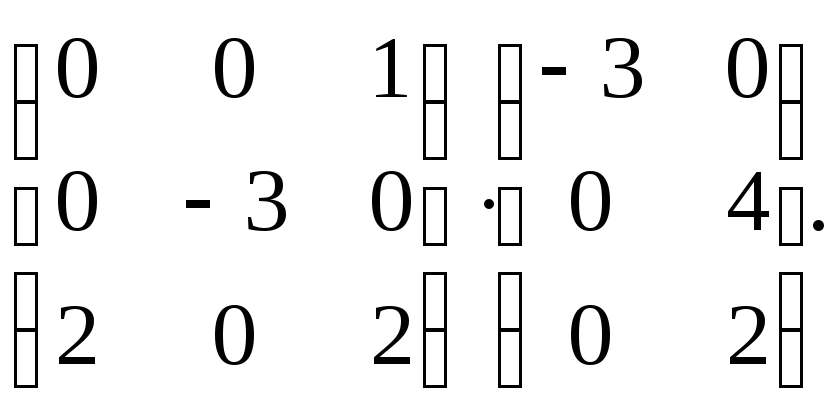
3. Найдите элемент с₂₁ матрицы С = АВ, если

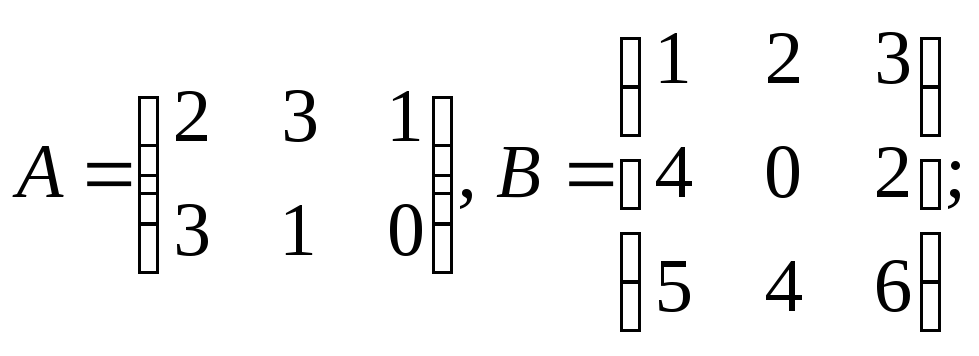
4. Решите уравнение .

5. Вычислите определитель: а) ; б) .

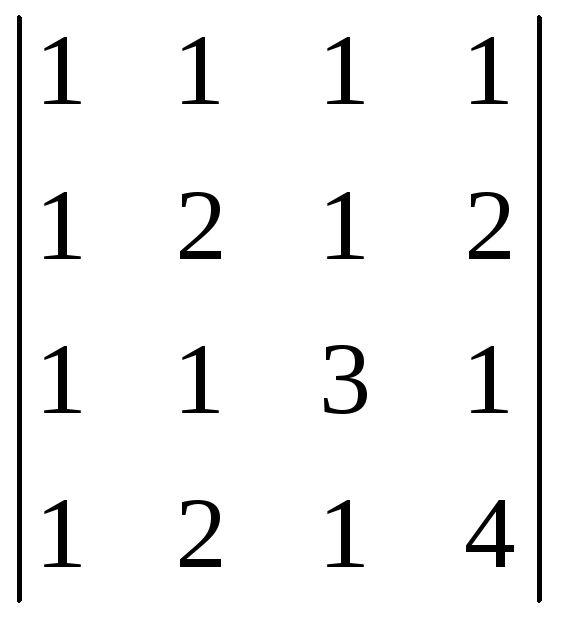6. При каких значениях параметра а матрица 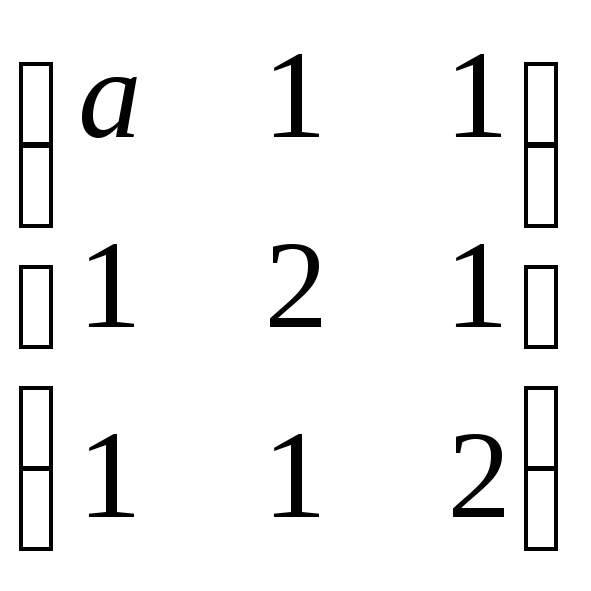не имеет обратной?

7. Решите систему уравнений:

а) 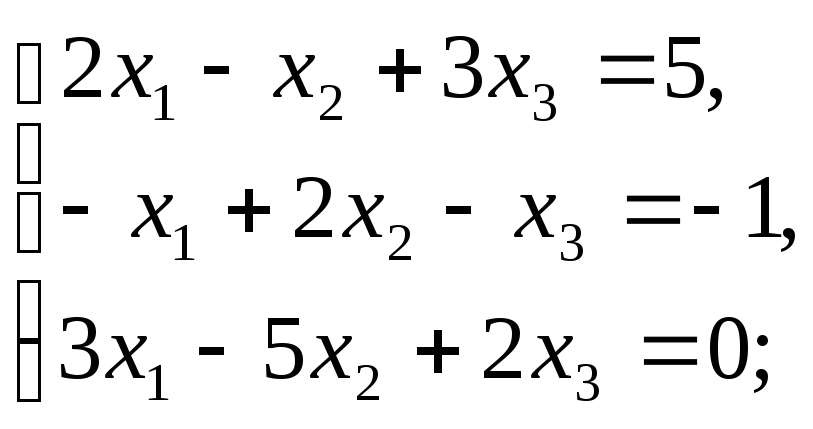б)

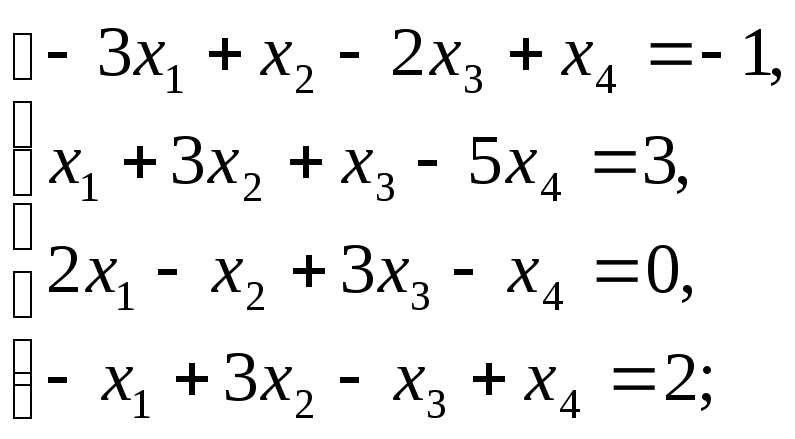в) г)

8. Даны векторы и . Найдите: а) ; б) .

9. Даны векторы . Найдите угол между векторами:

а) и ; б) и ; в) и .

10. Найдите угол между векторами и , если А(2;5;0), Р(−2;4;8), М(0;−1;5).

11. Найдите х, при котором векторы и перпендикулярны.

12. Даны векторы и . При каком значении m эти векторы коллинеарны?

13. На векторах и построен параллелограмм. Найдите длины диагоналей этого параллелограмма и косинус острого угла между ними, если .

14. Найдите вектор , cонаправленный с вектором , если известно, что .

15. Найдите вектор , коллинеарный вектору , если известно, что .

16. Исследуйте на линейную зависимость векторы:

1) ; 2) .

17. Разложите вектор по векторам , если это возможно.

18. Напишите уравнение прямой, проходящей через точку М(0;−2) перпендикулярно прямой x + 2y – 1 = 0.

19. Прямая проходит через середину отрезка, соединяющего точки А(−2;−2) и В(4;0), перпендикулярно этому отрезку. Составьте уравнение этой прямой.

20. Найдите расстояния от точек А(1;−2), В(0;−1) и С(2;−2) до прямой 2x + y − 2 = 0.

21. Даны вершины треугольника: А(−2;−4), В(−5;2), С(3;6).

1) Напишите уравнения прямых, содержащих стороны треугольника АВС.

2) Напишите уравнение прямой, содержащей медиану АМ и найдите ее длину.

3) Напишите уравнение прямой, содержащей высоту ВН и найдите ее длину.

4) Напишите уравнение прямой, содержащей среднюю линию MN (точка N – середина стороны СА), найдите ее длину.

5) Найдите расстояние от точки В до медианы АМ.

22. Изобразите на плоскости множество точек, координаты которых удовлетворяют системе линейных неравенств:

1) 2)

23. Что представляют собой геометрические места точек плоскости, заданные следующими уравнениями? Изобразите эти геометрические места точек.

1) 25x² + 9y² = 225; 2) 36y² − 9x²= 324;

3) x² + y² = 25; 4) x² − 16y² = 16;

5) у² = 5х; 6) 16x² + 25y² + 64x − 50y − 311 = 0.

24. Напишите уравнение плоскости, проходящей через точки М₁(−2;3;−5), М₂(1;2;−4) и М₃(5;0;−3).

25. Даны точки М₁(1;−3;5) и М₂(3;2;0). Напишите уравнение плоскости, проходящей через точку М₁ и перпендикулярной вектору .

26. Напишите уравнение прямой, проходящей через точку М(1;3;−2) и параллельной вектору .

27. Напишите уравнение прямой, проходящей через точки М₁(5;–3;2) и М₂(3;1;–2).

28. Определите взаимное расположение плоскостей: а) 2x – 3y – 4z + 11 = 0, –4x + 6y + 8z + 36 = 0;

б) 2x – 3z – 12 = 0, 4x + 4y – 6z + 7 = 0; в) 3x – 2y – 2z + 7 = 0, 2x + 2y + z + 4 = 0.

29. Найдите угол между плоскостями и .

30. Напишите уравнение плоскости, проходящей через точку М(2;–1;6) параллельно плоскости x + y – 2z + 5 = 0.

31. Найдите расстояние от точки А(3;9;1) до плоскости x – 2y + 2z – 3 = 0.

32. Напишите уравнение плоскости, проходящей через точку М(–1;–5;8) перпендикулярно прямой

.

33. Напишите уравнение прямой, проходящей через начало координат перпендикулярно плоскости, заданной уравнением 3x + 5z – 5 = 0.

Задания для самостоятельной работы

Вариант 1.1

1) Найдите произведения (если они существуют) АВ и ВА, где

2) Решите систему уравнений

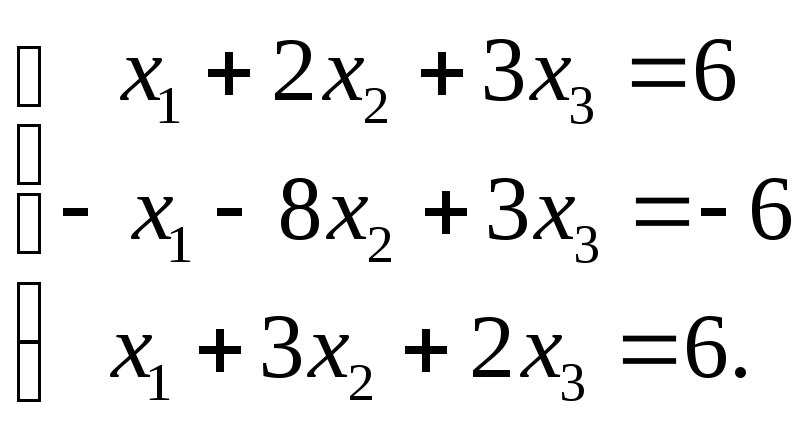
3) Найдите косинус угла между векторами и , если известно, что

4) Напишите уравнение прямой, проходящей через точку М(–3;2) параллельно прямой 3x + y – 1 = 0.

5) Какую линию на плоскости задает уравнение x² + 4y² = 36? Постройте эту линию в прямоугольной системе координат.

Вариант 1.2

1) Найдите произведения (если они существуют) АВ и ВА, где

2) Решите систему уравнений

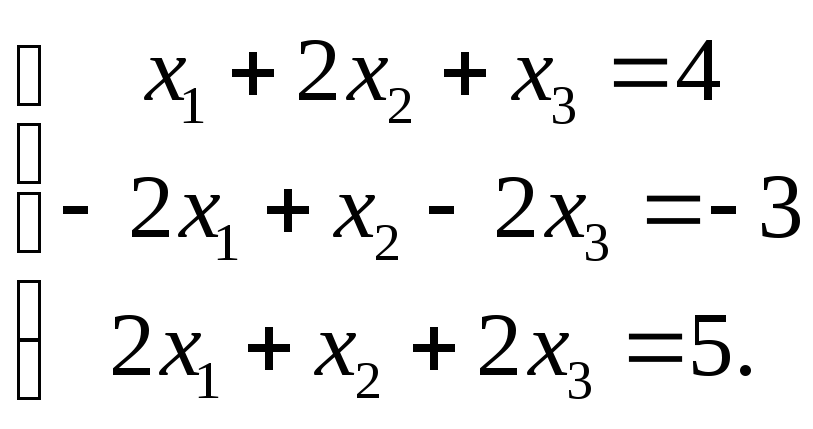
3) При каком значении параметра а векторы и будут коллинеарны?

4) Напишите уравнение прямой, проходящей через точку М(–2;–1) параллельно прямой 3x – 2y + 7 = 0.

5) Какую линию на плоскости задает уравнение ? Постройте эту линию в прямоугольной системе координат.

Вариант 2.1

1) Найдите матрицу C = 2AВ − 3B, если

2) Решите систему уравнений

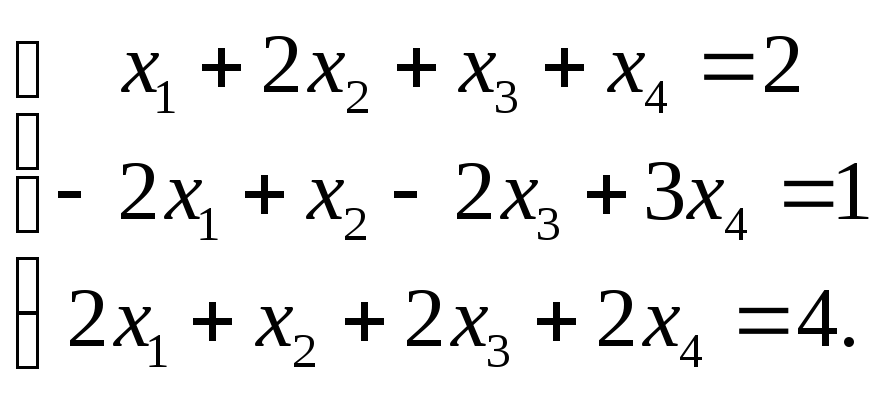
3) Найдите длину вектора , если известно, что

4) Напишите уравнение прямой, проходящей через точку М(0;–2) перпендикулярно прямой x – 2y + 5 = 0.

5) Какую линию на плоскости задает уравнение 6x² − 4y² = 36? Постройте эту линию в прямоугольной системе координат.

Вариант 2.2

1) Найдите матрицу C = 3AВ − 2А, если

2) Решите систему уравнений

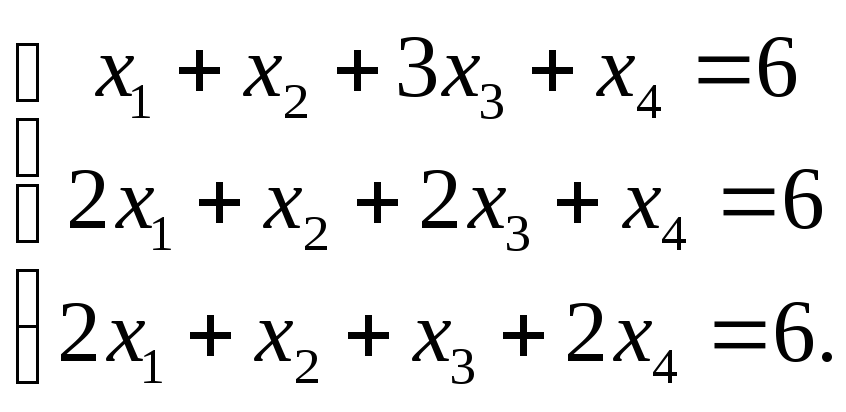
3) Найдите длину вектора , если известно, что А(1;0;2), В(–1;0;3), С(–2;–3;5).

4) Напишите уравнение прямой, проходящей через точку М(–1;3) перпендикулярно прямой x – 2y + 7 = 0.

5) Какую линию на плоскости задает уравнение ? Постройте эту линию в прямоугольной системе координат.

БИЛЕТ (образец)

1. а) Алгебраическое дополнение элемента матрицы. Разложение определителя матрицы по элементам любого столбца.

б) Вычислите сумму А₁₃ – А₃₂, где A_ij − алгебраическое дополнение соответствующего элемента матрицы

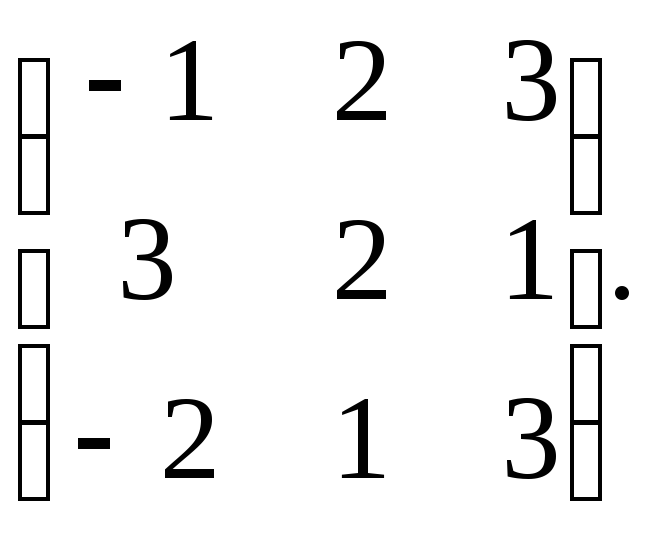
2. а) Теорема о том, что координаты точек, лежащих в одной полуплоскости относительно прямой, заданной уравнением Ax + By + C = 0, удовлетворяют одному из неравенств

Ax + By + C > 0, Ax + By + C < 0.

б) Не выполняя построение, выясните, пересекает ли прямая 3x – y + 5 = 0 отрезок АВ, где А(5;–1), В(–3;2).

3. 1) Найдите матрицу C = 3AВ − 2А, если

2) Решите систему уравнений

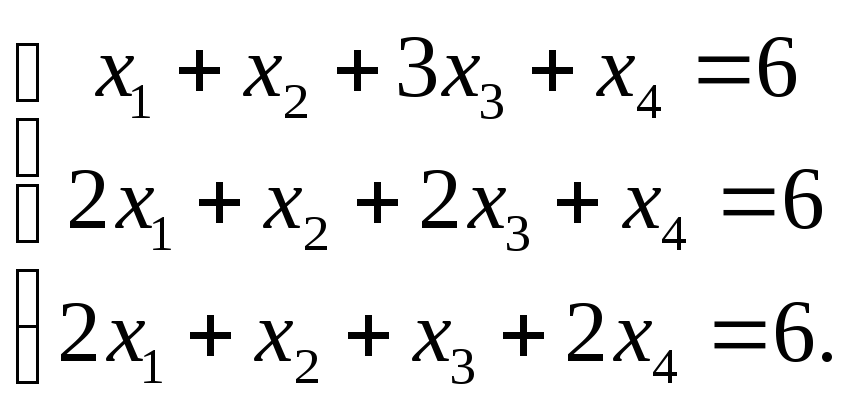
3) Найдите длину вектора , если известно, что А(1;0;2), В(–1;0;3), С(–2;–3;5).

4) Напишите уравнение прямой, проходящей через точку М(–1;3) перпендикулярно прямой x – 2y + 7 = 0.

5) Какую линию на плоскости задает уравнение ? Постройте эту линию в прямоугольной системе координат.