
Учебное пособие по ТВ и МС
.pdf
P( AB) = P( A)P(B / A) = P(B)P( A / B). |
(1.6) |
Формула (1.6) носит название формулы произведения вероятностей, а
само утверждение – теоремой умножения вероятностей. Она обобщается на случай произвольного числа событий:
P( A1 A2 KAn ) = P( A1 )P( A2 / A1 )P( A3 / A1 A2 )KP( An / A1 A2 KAn−1 ). |
(1.7) |
Упражнение 1.5. Доказать формулу произведения вероятностей (1.7) методом математической индукции.
1.9. Формула полной вероятности и формула Байеса
Пример 1.12. Есть три завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод − 35% и 3-й завод − 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода.
Вся продукция смешивается и поступает в продажу. Найти: а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1-м заводом, если это изделие бракованное.
Решение. Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть 0,05 0,25 + 0,03 0,35 + 0,04 0,4. Вторая вероятность равна доле брака 1-го заводасреди всего брака, то есть
0,05 0,25 . 0,05 0,25 + 0,03 0,35 + 0,04 0,4
Определение 1.6. Набор событий (называемых часто гипотезами) B1, … , Bn
называется полной группой событий или разбиением пространства Ω, если
n
∑ Bi = Ω и i ≠ j Bi IBj = .
i=1
Очевидно, что любые два противоположных события A и A образуют полную группу событий, т.е. P( A + A) = P(Ω) = 1.
21
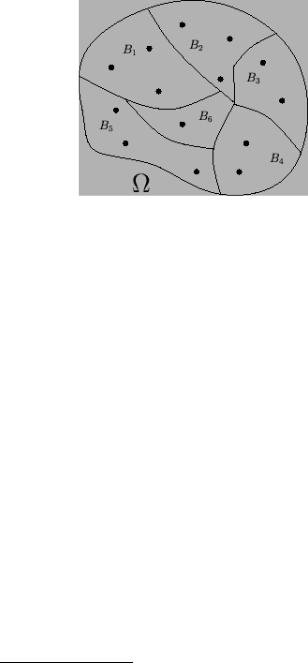
Рис 1.7. Разбиение пространства Ω
Предложение 1.3. (Формула полной вероятности). Пусть события B1, … ,
Bn образуют разбиение. Тогда
n
P( A) = ∑ P( A / Bi )P(Bi ).
i=1
Доказательство. Справедливо представление
A = AB1 +K+ ABn .
Следовательно, P(A) = P(AB1) +K+ P(ABn ). Для завершения доказательства достаточно применить формулу произведения вероятностей (1.6).
Предложение 1.4. (Формула Байеса). Пусть B1, … , Bn – разбиение. Тогда
P(Bk / A) = nP( A/ Bk )P(Bk ) . #
∑P( A/ Bi )P(Bi )
i=1
Упражнение 1.6. Вывести формулу Байеса.
Указание: воспользоваться определением условной вероятности и применить формулу полной вероятности.
1.10. Независимость событий
Определение 1.7. События A и B называются независимыми, если
P( AB) = P( A) P(B).
Замечание 1.6. Если A и B независимы и P(B) > 0, то
22

P( A / B) = |
P( AB) |
= |
P( A)P(B) |
= P( A). |
|
P(B) |
P(B) |
||||
|
|
|
Аналогично, если A и B независимы и P(A) > 0, то P(B / A) = P(B).
Пример 1.13. Бросание двух игральных костей.
Ω = {(a1, a2): a1, a2 {1, … , 6}}, |Ω| = 36,
A = {на первой кости выпала «6»},
B = {на второй кости выпала «6»},
A = {(6,1), (6,2), … , (6,6)}, |A| = 6,
B = {(1,6), (2,6), … , (6,6)}, |B| = 6, AB = {(6,6)}, |AB| = 1.
P(A) = 
 ΩA
ΩA
 = 366 = 16 , P(B) =
= 366 = 16 , P(B) = 
 ΩB
ΩB
 = 366 = 16 , P(AB) = ABΩ = 361 .
= 366 = 16 , P(AB) = ABΩ = 361 .
Таким образом, справедливо равенство P( AB) = P( A) P(B), и события A и B – независимы.
Упражнение 1.7. Известно, что события A и B независимы. Доказать независимость событий A и B. Показать, что отсюда будет следовать, что: A и B – независимы, A и B – независимы.
Упражнение 1.8. Доказать следующее утверждение. Если события A и B несовместны, то они независимы, если и только если P(A) = 0 или P(B) = 0.
1.11. Статистическая независимость
Теперь распространим понятие независимости на случай произвольного конечного набора событий A1, … , An. Обсудим два способа распространения
определения 1.7, а именно, понятия взаимной независимости и попарной независимости.
Определение 1.7. События A1, … , An называются независимыми в
совокупности, если для всех k (1 ≤ k ≤ n) и для любых 1 ≤ i1 < … < ik ≤ n |
верно |
|||
P( Ai |
KAi |
) = P(Ai |
)KP(Ai ). |
(1.8) |
1 |
k |
1 |
k |
|
Рассмотрим теперь второе, более слабое определение независимости.
23

Определение 1.8. События A1, … , An называются попарно независимыми,
если i ≠ j P(Ai Aj ) = P(Ai ) P(Aj ).
Замечание 1.7. Понятия взаимной независимости и попарной независимости набора событий не являются равносильными, а именно,
Взаимная независимость / Попарная независимость.
Первая импликация вытекает из определений 1.7 и 1.8, достаточно взять в равенстве (1.8) n = 2. Следующие два примера показывают, что события могут быть попарно независимыми, но зависимыми в совокупности.
Пример 1.14. Производится бросание двух костей. Рассмотрим следующие события:
A = {на первой кости выпало нечетное число очков},
B = {на второй кости выпало нечетное число очков}, C = {сумма очков – нечетна}.
События A, B, C – попарно независимые. Действительно,
P(A) = P(B) = P(C) = 12 , P(AB) = P(AC) = P(BC) = 14 .
Но независимости в совокупности нет, т.к.
ABC = P(ABC) = 0 ≠ |
1 |
= P(A)P(B)P(C). |
|
8 |
|||
|
|
Пример 1.15. (Пример С.Н. Бернштейна). Рассмотрим правильный тетраэдр, три грани которого окрашены, соответственно, в красный, синий и зеленый цвета, а четвертая грань содержит все три цвета. Событие A (В,С) означает, что выпала грань, содержащая красный (синий, зеленый) цвета.
Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность пересечения любых двух из них равна 1/4, т.к. как только одна грань содержит два цвета. А т.к. 1/4 = 1/2 1/2, то все события попарно независимы.
Но вероятность пересечения всех трех тоже равна 1/4, а не 1/8, то есть события не являются независимыми в совокупности.
Заметим, что (1.8) выполнено для k = 2, но не выполнено для k = 3.
Пример 1.16. Важный пример независимых в совокупности событий возникает в схеме испытаний Бернулли. Как и в примере 1.6, рассмотрим события Ai = {i-е испытание закончилось «успехом»}.
24
Из упражнений 1.2 и 1.3 вытекает, что |
P(Aj |
KAj |
) = P(Aj |
)KP(Aj ) = pk |
|
1 |
k |
1 |
k |
для любого поднабора индексов {j1, … , jk} {1, … , n}. Следовательно, события A1, … , An независимы в совокупности. Поэтому, впредь мы будем говорить, что схема Бернулли является моделью последовательности независимых испытаний Бернулли.
Глава 2. Дискретные случайные величины и их распределения
Для дальнейшего необходимо ввести понятие дискретного вероятностного пространства. Мы будем называть дискретным вероятностным пространством либо конечное вероятностное пространство, определенное в § 1.2, либо счетное вероятностное пространство, которое мы определим ниже.
2.1. Счетное вероятностное пространство
Пусть Ω – счетное множество, то есть, бесконечное множество, элементы которого могут быть занумерованы натуральными числами:
Ω={ω1,ω2 ,K,ωn ,K} ={ωi }i N ,
афункция P, зависящая от ω Ω, удовлетворяет следующим условиям:
|
∞ |
P(ω) ≥ 0 , ∑P(ω) = ∑P(ωi ) =1. |
|
ωΩ |
i=1 |
В этом случае говорят, что (Ω, P) – счетное вероятностное пространство.
Как и прежде, событиями будем называть любые подмножества множества элементарных исходов Ω: A Ω.
2.2. Дискретные случайные величины
Определение 2.1. Случайной величиной назовем произвольную функцию на множестве элементарных исходов: ξ : Ω → R, ξ = ξ(ω).
Множества вида {ω: ξ(ω) = x} Ω являются событиями. Иногда для них будем использовать более короткое обозначение: {ξ = x} =& {ω : ξ(ω) = x} .
Так как Ω – не более чем счетно, то случайная величина ξ принимает не более чем счетное число значений: x1, x2, … , xk, … .
25

Определение 2.2. Распределением дискретной случайной величины ξ назовем таблицу:
ξ |
x1 |
x2 |
P |
p1 |
p2 |
… xk …
… pk …
где pk = P{ω:ξ(ω) = xk } = P{ξ = xk }.
Замечание 2.1. Если k ≠ l, то {ξ = xk} ∩ {ζ = xl} = . Более того,
U{ω :ξ(ω) = xk } = Ω . Следовательно, ∑pk =1.
k k
2.3.Схема Бернулли
2.3.1.Распределение числа успехов в n испытаниях
Определение 2.3. Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода – «успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью р [0,1], «неудача» – с вероятностью q = 1 – р.
Определение 2.4. Бернуллиевской называют случайную величину, принимающую два значения:
ξ = |
с |
вероятностью |
p , |
1, |
|||
0, |
с |
вероятностью |
1− p . |
Таким образом, ее распределению соответствует следующая таблица.
ξ |
0 |
1 |
|
|
|
P |
1 − p |
p |
|
|
|
Предложение 2.1. (Формула Бернулли). Обозначим, через vn число успехов в n испытаниях схемы Бернулли. Тогда для любого k = 0,1,... , n
P(vn = k) = Pn (k) = Cnk pk (1 − p)n −k = Cnk pk qn −k .
Доказательство. Событие А = {vп=k} означает, что в п испытаниях схемы Бернулли произошло ровно k успехов (и, соответственно, (n−k) неуспехов). Рассмотрим один из благоприятствующих событию A элементарных исходов:
26

|
|
|
|
y, y,Ky,н, н,K.н |
|||
|
14243 |
14243 |
. |
|
k |
л−k |
|
Поскольку испытания независимы, вероятность такого элементарного исхода (первые k испытаний завершились успехом, остальные неудачей) равна pk (1−p)n−k.
Другие благоприятствующие событию A элементарные исходы отличаются от рассмотренного выше лишь расположением k успехов на n
местах. Есть ровно Cnk способов расположить k успехов на n местах. Поэтому событие A состоит из Ck элементарных исходов, вероятность каждого из которых равна pk (1−p)n−k.
Определение 2.5. Набор чисел P(vn = k) = Ckpk(1−p)n−k, k = 0,1,…,n
называется биномиальным распределением вероятностей и обозначается
Bn,p или B(n,p). Случайную величину с этим законом распределения называют биномиальной. Она означает, что в п испытаниях схемы Бернулли произошло ровно k успехов и (n−k) неуспехов.
Биномиальному распределению вероятностей соответствует таблица:
νn |
0 |
1 |
… |
k |
… |
n |
P |
(1 − p)n |
np(1 − p)n−1 |
… |
Cnk p k (1 − p)n−k |
… |
p n |
|
|
|
|
|
|
|
Определение 2.6. Будем говорить, что случайная величина Π имеет
пуассоновское распределение с параметром λ > 0, если она принимает целые неотрицательные значения со следующими вероятностями:
P{Π = k}= |
λk |
e−λ , k = 0, 1, K. |
|
k! |
|
2.3.2. Наиболее вероятное число успехов
По формуле Бернулли, событие «произошло 0 успехов в п испытаниях» имеет вероятность qn, 1 успех − вероятность npqn−1 и т.д. Какое же число успехов наиболее вероятно? Иначе говоря, при каком k достигается максимум P(vn = k)?
Предложение 2.2. В n испытаниях схемы Бернулли с вероятностью успеха p наиболее вероятным числом успехов является
а) единственное число k0 = [np + p], если число np + p не целое; б) два числа k0 = np + p и k0 = np + p − 1, если число np + p целое.
27
Доказательство. Чтобы выяснить это, сравним отношение P(vn = k) и P(vn = k−1) с единицей:
P(vn = k) |
= |
n! |
(k −1)!(n − k +1)! |
|
p k qn −k |
||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
||
P(vn = k −1) |
k!(n − k)! |
|
|
n! |
|
|
p k −1 q n−k +1 |
||||||
|
= |
(n −k +1) p |
=1+ |
(n −k +1) p |
|
−1 =1+ |
np + p −k |
. |
|||||
|
|
kq |
|
|
|||||||||
|
|
|
kq |
|
|
|
|
|
kq |
||||
Видим, что
(a) Р(vn = k) > Р(vn = k − 1) при np + p − k > 0, то есть при k < np + p; (b) Р(vn = k} < Р(vn = k − 1) при np + p − k < 0, то есть при k > np + p;
(c) P(vn = k) = P(vn = k − 1) при np + p − k = 0, что возможно лишь если пр + р − целое число.
Рассмотрим два случая: пр + р Z и пр + р Z. В первом случае пусть k0 = пр + р. Из полученных выше неравенств сразу следует, что
(a) |
(c) |
(b) |
|
K< P(vn = k0 − 2) < |
P(vn = k0 −1) = P(vn = k0 ) > P(vn = k0 |
+1) >K |
|
Во втором случае пусть k0 = [пр + р] (целая часть числа пр + р, то есть наибольшее целое число, не превосходящее пр + р). Из неравенств (а), (b) следует, что
(a) |
(a) |
(b) |
|
K< P(vn = k0 − 2) < |
P(vn = k0 −1) < |
P(vn = k0 ) > P(vn = k0 |
+1) >K |
Действительно, неравенство Р(vn = k0) > Р(vn = k0 − 1), например, следует из (b), примененного для k = k0 − 1 > np + p.
В зависимости от того, является число пр + р целым или нет, имеем либо два равновероятных «наиболее вероятных» числа успехов k0 = пр + р и k0 − 1 = пр + р − 1, либо одно «наиболее вероятное» число успехов k0 = [пр + р].
Замечание 2.1. В предложении 2.2 наиболее вероятное число успехов k0 можно находить из двойного неравенства
np − q ≤ k0 ≤ np + p .
Пример 2.1. Если p = q = 1/2, то при четном числе испытаний n число np + р = (п+1)/2 Z − не целое, так что наиболее вероятным является единственное число успехов [(п+1)/2] = n/2. Что совершенно понятно, так как есть нечетное число возможностей – получить 0,1, ... , п успехов, причем вероятности получить k и п−k успехов одинаковы.
28
При нечетном же числе испытаний п число пр + р = (п+1)/2 Z − целое, так что наиболее вероятными (и одинаково вероятными) являются два числа успехов (п+1)/2 и (п−1)/2.
Пример 2.2. Вероятность появления события A в каждом из n независимых испытаний равна 0,7. Сколько таких испытаний нужно произвести, чтобы наиболее вероятное число появлений события A в производимых испытаниях k0 = 20?
Решение. По условию p = 0,7 и q = 0,3. Тогда из замечания 2.1 получим
0,7n − 0,3 ≤ 20 ≤ 0,7n + 0,7 .
Это двойное неравенство равносильно системе неравенств
0,7n − 0,3 ≤ 20,0,7n + 0,7 ≥ 20.
Из первого неравенства системы имеем n ≤ 20,3/ 0,7 = 29 . Из первого неравенства системы найдем n ≥19,3/ 0,7 ≈ 27,57 . Отсюда следует, что необходимо произвести 28 или 29 испытаний.
2.3.3. Номер первого успешного испытания
Рассмотрим схему Бернулли с вероятностью успеха p в одном испытании. Испытания проводятся до появления первого успеха. Введем величину τ,
равнуюномерупервогоуспешногоиспытания.
Предложение 2.3. Вероятность того, что первый успех произойдет в испытании с номером k N = {1, 2, 3,…}, равна P(τ = k) = pqk −1 .
Доказательство. Действительно, |
P(τ = k) = P(н,н,K,ну) = pqk −1 . |
|
||
|
14243 |
|
||
|
|
k −1 |
|
|
Определение 2.7. Набор чисел |
{pqk −1 , k =1,2,3,L} |
называется |
||
геометрическим распределением вероятностей и обозначается Gp или G(p).
Геометрическое распределение вероятностей обладает интересным свойством «нестарения», заключающимся в следующем.
Пусть величина τ обозначает время безотказной работы (измеряемое целым числом часов) некоторого устройства. Предположим, что для величины τ вероятность принять любое свое значение k равна pqk−l, т.е. P(τ = k) = рqk−l
для любого k N. Тогда для произвольных n, k ≥ 0
29
P(τ > n + k /τ > n) = P(τ > k). |
(2.1) |
Формула (2.1) означает следующее. Если известно, что устройство уже проработало без отказа n часов, то вероятность ему работать еще не менее k часов точно такая же, как вероятность проработать не менее k часов для нового устройства.
2.4. Математическое ожидание
Так как случайная величина ξ может принимать различные значения ξ(ω), в зависимости от того, какой исход ω «виртуального» эксперимента (замечание 1.1) будет разыгран, то с разных точек зрения удобно иметь числовую характеристику, имеющую смысл «среднего значения» случайной величины.
Определение 2.8. Математическим ожиданием дискретной случайной величины ξ называется число
M [ξ]= ∑ξ(ω)P(ω) .
ωΩ
Математическое ожидание существует в том и только в том случае, когда этот ряд сходится абсолютно.
Предложение 2.4. Математическое ожидание может быть вычислено по формуле
M [ξ]= ∑ xk pk = ∑ xk P{ξ = xk }. |
(2.2) |
|
k |
k |
|
Доказательство. Мы будем использовать следующий факт из курса математического анализа. Пусть дан абсолютно сходящийся ряд. Тогда его члены можно произвольным образом переставлять и группировать, полученные в результате этого ряды будут сходиться к одному и тому же значению:
M [ξ]= ∑ξ(ω)P(ω) = ∑ ∑ xk P(ω) =
ωΩ |
|
k ω: ξ (ω)=xk |
= ∑ xk |
∑ P(ω) =∑ xk P{ω :ξ(ω) = xk }. |
|
k |
ω:ξ (ω)=xk |
k |
Пример 2.3. Математическое ожидание бернуллиевской случайной величины:
30
