1.4. Дифференциальный метод обработки данных

Этот метод применяется при обработке экспериментальных данных, полученных в РИС-Н и РИС-П. РИВ может применяться только при измерении концентрации реагентов по длине реактора. В РИС-Н концентрации реагентов не изменяются во времени, и поэтому скорость реакции может быть рассчитана непосредственно по разности значений концентраций на входе и выходе из него. В связи с этим реактор такого типа называется дифференциальным.

Для рассматриваемого примера в случае проведения реакции в РИС-Н скорости реакции по реагентам A и Y равны:

Затем выдвигается предположение о форме кинетического уравнения. Допустим, что уравнение для скорости расходования реагента Y имеет следующий вид:

Прологарифмировав его, получим:

lnr_Y=lnk_Y + n_Alnc_A + n_Ylnc_Y.

Таким образом, исходное нелинейное (степенное) уравнение преобразовано к линейному виду (уравнению прямой линии). Эта операция называется линеаризацией. Проведя ряд экспериментов при разных относительных временах пребывания, получают набор разностей концентраций реагентов и соответствующий ему набор скоростей. Далее решают полученную систему уравнений и определяют все коэффициенты уравнений (т.е. порядки реакции по реагентам и константу скорости, выраженную по реагенту Y).

При проведении экспериментов в РИС-П концентрации реагентов изменяются во времени, и в результате получается набор первичных кинетических кривых. Такие кривые называют интегральными, так как подобного рода зависимости могут быть получены интегрированием дифференциальных уравнений скорости. Соответственно, и реакторы, в которых их получают, называются интегральными. Суть дифференциального метода в данном случае заключается в дифференцировании первичных кинетических кривых в выбранных точках с расчетом скорости реакции по выбранным реагентам. Далее так же выдвигается гипотеза о форме кинетического уравнения, проводится операция линеаризации, и рассчитываются коэффициенты линейного уравнения.

При проведении реакции в РИВ получают первичные кривые изменения концентрации реагентов по длине реактора. Такой реактор также является интегральным. Зная скорость течения жидкости через реактор и его сечение, проводят перерасчет и получают зависимости концентраций от времени пребывания:

w=l/; dl=wd;

Далее обработку проводят, как в РИС-П. Основной недостаток дифференциального метода – его низкая точность.

1.5. Интегральный метод обработки экспериментальных данных

Этот метод предусматривает определение вида кинетических уравнений в форме зависимости концентрации реагентов от времени. Так как подобного рода зависимость трудно получить непосредственно, то чаще всего выдвигается гипотеза о дифференциальной форме кинетического уравнения, которое интегрируется при некоторых значениях параметров. Сопоставление экспериментальных и расчетных данных позволяет сделать вывод о правильности выдвинутой гипотезы и наоборот. Метод используется при обработке экспериментальных данных, полученных в интегральных реакторах (РИС-П, РИВ).

Предположим, что для рассматриваемых реакций уравнение для скорости расходования вещества Y имеет вид:

Так как реагент А расходуется по двум реакциям, его текущую концентрацию нельзя выразить через текущую концентрацию вещества Y, а, следовательно, невозможно проинтегрировать это уравнение непосредственно. Однако если взять реагент А в таком количестве, чтобы в течение эксперимента его концентрация практически не изменялась(с_А0>>c_Y0), то уравнение можно упростить (понизив общий порядок реакции):

Полученное уравнение можно проинтегрировать, если предварительно задаться порядком реакции по веществу Y. Общий вид решения дифференциального уравнения имеет следующий вид:

Чаще всего полученные решения линеаризуют (приводят к линейному виду y=a+bx), как показано в табл. 3.

Таблица 3

Линеаризация кинетических уравнений, х=

Порядок реакции nА	y	a	b
0	сА	сА,0	–k
0,5	сА	сА,0	–k/2
1	lnсА	lnсА,0	–k
1,5	1/сА	1/сА,0	k/2
2	1/сА	1/сА,0	k

Проводя эксперименты, в которых последовательно изменяются начальные концентрации реагентов, входящих в кинетическое уравнение, определяют порядки реакции и константу скорости реакции. Сопоставление расчетов по полученному уравнению с экспериментальными данными позволяет судить о достоверности полученного описания.

Как правило, кинетические уравнения удается линеаризовать. Экспериментально полученные порядки обычно кратны 0,5. Следует только помнить, что полученные уравнения применимы в исследованном диапазоне изменения параметров процесса и экстраполяции не всегда дают правильные результаты. Более подробную информацию о кинетическом моделировании можно отыскать в специальной литературе.

Если речь идет о сложных реакциях, то на первом этапе их исследования обычно устанавливают последовательность превращения реагентов, анализируя форму кинетических кривых и относительные скорости образования и расходования участников реакции. Таким путем можно выяснить, какие из наблюдаемых стадий являются последовательными, а какие параллельными. Предварительную оценку такого рода часто можно сделать по форме кинетических кривых. Пусть у нас есть исходное вещество А, из которого образуются продукты В и С. Если концентрация одного из веществ (например, В) в течение реакции проходит через максимум, то оно участвует в стадиях последовательного превращения. При этом кинетическая кривая продукта, получающегося только из вещества В, имеет S-образный вид, и начальная скорость его накопления равна нулю (рис. 5,а). Если В и С образуются из А параллельными путями, то начальные скорости их образования обе будут отличны от нуля (рис. 5,б). Более сложен для анализа случай последовательно-параллельного образования продуктов. В этом случае одна из кинетических кривых продуктов (В) проходит через максимум, а скорость накопления С при =0 не равна нулю (рис. 5,в). После предварительной оценки последовательности превращений А можно исследовать реакции индивидуального промежуточного продукта В в отсутствие А.

Рис. 5. Кинетические кривые последовательной (а), параллельной (б) и последовательно-параллельной реакций (в)

Для параллельных реакций часто вводят понятие дифференциальной (мгновенной) селективности. Дифференциальная селективность  это отношение скорости превращения исходного вещества в заданный продукт к общей скорости его расходования.

Например, для реакций:

_1AA_BB; _2AA_zZ

дифференциальная селективность составит:

Интегральная селективность при этом равна:

Связь между дифференциальной и интегральной селективностью может быть представлена и следующим образом:

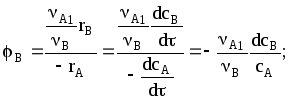
Если проинтегрировать это уравнение с разделенными переменными, получим после преобразований

А

Обратившись к формуле интегральной селективности для реакций, протекающих при постоянном объеме,

мы увидим, что она отличается от выражения в левой части А на множитель Х_А, стоящий в знаменателе. Таким образом,

Отсюда понятно, что интегральная селективность, выражающая соотношения количеств продуктов, образующихся в реакциях (в частности, параллельных), определяется соотношением скоростей накопления этих продуктов. С увеличением степени превращения исходных реагентов может наблюдаться рост, падение или неизменность интегральной селективности вследствие разных законов изменения скоростей параллельных реакций.