Фазовые равновесия и фазовые переходы

План

Фазы вещества. Равновесие фаз. Фазовая диаграмма (диаграмма состояния). Тройная точка. Уравнение Клайперона – Клаузиуса.

Фазой называется макроскопическая физически однородная часть вещества, отделённая от остальных частей системы поверхностью раздела. Фазовое равновесие – одновременное существование фаз в многофазной системе (без изменения одной фазы за счет другой).

Разные фазы одного и того же вещества могут находиться в равновесии, соприкасаясь друг с другом. Такое равновесие наблюдается лишь в ограниченном интервале температур, причём каждому значению температуры соответствует своё значение давления , при котором возможно равновесие. Совокупность состояний равновесия 2-х фаз изображается на диаграммелинией.Три фазы одного и того же вещества (твёрдая, жидкая и газообразная или жидкая и две твёрдых или три твёрдых) могут находиться в равновесии только при единственных значениях температуры и давления, которые на диаграмме соответствует точка, называемая тройной.

В термодинамике доказывается, что равновесие более чем 3-х фаз одного и того же вещества невозможно (и это подтверждено экспериментально).

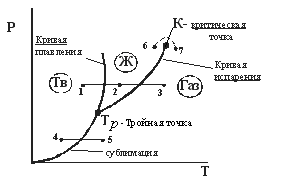
Диаграмма состояния. (рис. 12.1)

	1-2-3 переход кристаллжидкостьгаз 4-5 кристалл газ 6-7 переход из жидкости в газ без расслоения на фазы.
Рис. 12.1

Определение. Сублимация (возгонка) – непосредственный (без плавления) переход из кристаллического состояния в газообразное.

Из диаграммы (рис. 12.1) следует, что жидкая фаза может находиться в равновесии при давлениях не меньше, чем давление в тройной точке .Например, в случае углекислоты ()=5,11 атм, поэтому при атмосферном давлении (1 атм.) углекислота может существовать только в твёрдом и газообразном состояниях.Твёрдая углекислота (называемая сухим льдом) на воздухе сублимирует, а не тает (переход 4-5). Для большинства же обычных веществ значительно меньше атмосферного давления (например, для=4,58 мм. рт. ст.), поэтому переход из кристаллического состояния в газообразное осуществляется через жидкую фазу.

Кривая испарения заканчивается в критической точке К. Поэтому возможен процесс в обход критической точки К. в этом случае переход из жидкого состояния в газообразное совершается непрерывно (процесс )без расслаивания на две фазы. При температурах выше критической вещество не может быть сжижено никаким сжатием.

Фазовые переходы с поглощением или выделением скрытой теплоты перехода называются фазовыми переходами первого рода. Например, в процессах плавления или кристаллизации. Фазовые переходы, не связанные со скрытой теплотой перехода, называются фазовыми переходами второго рода. Например, переход парамагнетик – ферромагнетик.

Уравнение Клапейрона – Клаузиуса

(без вывода).

теплота фазового перехода, температура,иобъёмы обеих фаз. (и,относятся к одному и тому же количеству вещества, например, к 1 молю или 1 кг, т.е. является удеальными).

определяет наклон фазовой кривой фазового равновесияР(Т). Уравнение Клапейрона – Клаузиуса даёт изменение температуры фазового перехода при изменении давления.

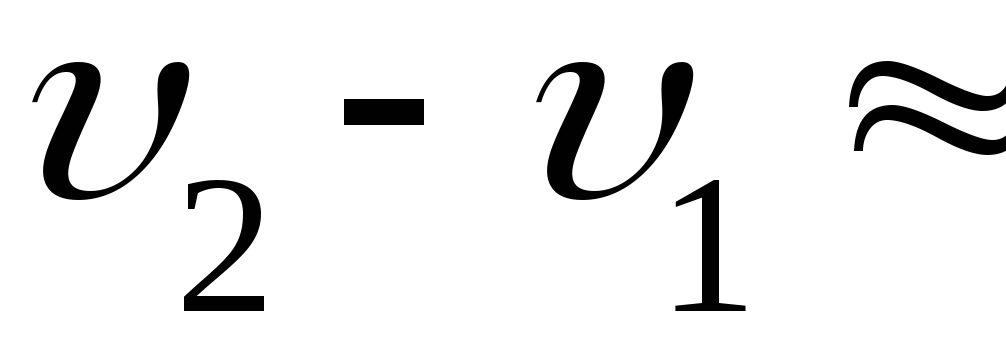
Пример. Для воды (льда) теплота плавления . Разница удельных объёмов льда и воды при 0(легко найти из соответствующих плотностей).

. То есть, с увеличением давления на одну атмосферу точка плавления льда понижается примерно на 0,0075 град.

Опыт. Если на брусок льда, лежащий своими концами на неподвижных опорах, накинуть проволочную петлю, и к ней подвесить тяжёлый груз, то лёд под проволокой плавится. Вода выдавливается из-под проволоки и замерзает над ней. Проволока постепенно проходит через брусок, однако брусок остаётся неразрезанным.

Вопросы для самоконтроля.

1. Что называется фазой?

2. Нарисуйте фазовую диаграмму состояния в Р-Т координатах. Ука-

жите на ней тройную точку. Каков ее смысл?

3. Приведите примеры фазовых переходов и укажите их на диаграмме

состояния.

4. Запишите уравнение Клапейрона – Клаузиуса. Какие величины оно

связывает? Приведите пример использования этого уравнения.

Лекция №7 (13)