Лекция №14

Первое начало термодинамики

План

1. Основные термодинамические понятия: внутренняя энергия, работа, теплота. Уравнение первого начала термодинамики.

2. Применение первого начала термодинамики к изопроцессам идеального газа. Зависимость теплоёмкости идеального газа от вида процесса. Формула Майера.

3. Работа, совершаемая газом при изопроцессах.

4. Адиабатический процесс. Политропические процессы.

1. Основные термодинамические понятия

Термодинамикав отличие от молекулярно-кинетической теории не вдаётся в рассмотрение микроскопической картины явлений (оперирует с макропараметрами). Термодинамика рассматривает явления, опираясьна основные законы (начала), которые являются обобщением огромного количества опытных данных.

Внутренняя энергия – энергия физической системы, зависящая от еёвнутреннего состояния. Внутренняя энергия включает энергиюхаотического (теплового) движениявсех микрочастиц системы (молекул, атомов, ионов и т.д.)и энергию взаимодействия этих частиц. Кинетическая энергия движения системы как целого и её потенциальная энергия во внешних силовых полях во внутреннюю энергию не входит. В термодинамике и её приложениях представляет интересне само значениевнутренней энергии, аеё изменениепри изменении состояния системы. Внутренняя энергия – функция состояния системы.

Работатермодинамической системы над внешними телами заключаетсяв изменении состояния этих тели определяется количеством энергии, передаваемой системой внешним телам при изменении объема.

	Работа в термодинамике не является полным дифференциалом (не является функцией состояния, а зависит от пути) и обозначается . Для того чтобы изменить объём, занимаемый газом, надо совершить работу. Представим себе газ, заключённый в цилиндрический объём с поршнем, движением которого изменяется объём газа (рис. 14.1).
Рис. 14.1

Сила, создаваемая давлением газа на поршень площадиравна. Работа, совершаемая при перемещении поршня, равна, гдеизменение объёма газа (рис. 14.1), то есть

Теплота (количество теплоты) – количество энергии, получаемой или отдаваемой системой при теплообмене. Элементарное количество теплоты не является в общем случае дифференциалом какой-либо функции параметров состояния. Передаваемое системе количество теплоты, как и работа, зависит от того, каким способом система переходит из начального состояния в конечное. (В отличие от внутренней энергии, для которой , но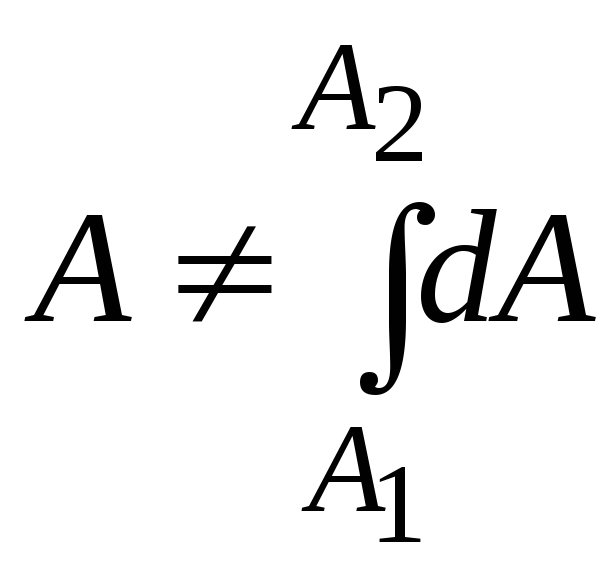, нельзя сказать, сколько работы содержит тело, “это функция” процесса – динамическая характеристика).

1-ый закон (начало) термодинамики: количество теплоты, сообщённое системе, идёт на приращение внутренней энергии системы и на совершение системой работы над внешними телами.

где количество сообщённой телу теплоты;

и начальное и конечное значения внутренней энергии;

работа, совершённая системой над внешними телами.

В дифференциальной форме 1-ое начало:

сообщённое телу элементарное количество теплоты;

изменение внутренней энергии;

совершённая телом работа (например, работа, совершённая при расширении газа).

2. Применение 1-го начала термодинамики к изопроцессам идеального газа

(Изопроцессы от (греч.) – равный). Процессы, происходящие при каком-то постоянном параметре (изотермический;изобарический;изохорический).

Теплоёмкостью тела называется величина, равная отношению сообщённого телу количества теплоты к соответствующему приращению температуры.

Размерность теплоёмкости тела .

Аналогичные определения вводятся для 1 моля (молярная теплоёмкость

), и для единицы массы вещества .

1. Рассмотрим нагревание газа при постоянном объёме. По первому закону термодинамики:

, т.к. , то.

по определению, а для процесса с:

, где

теплоёмкость газа при постоянном объёме.

Тогда и

2. Теплоёмкость газа при постоянном давлении:

.

Для идеального газа для 1 моля (из уравнения Менделеева-Клапейрона).

.

Продифференцируем это выражения по температуре Т, получим:

, получим для 1 моля

Но выражение называется уравнением Майера. Оно показывает, что всегда большена величину молярной газовой постоянной. Это объясняется тем, чтопри нагревании газа при постоянном давлении по сравнению с процессом при постоянном объёме, требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.

3. При адиабатическом процессе (процесс протекающий без теплообмена с внешней средой).

, , т.е. теплоёмкость в адиабатическом процессе равна нулю.

4. При изотермическом процессе ,, и, следовательно, теплоёмкость.

Существуют процессы, при которых газ, расширяясь, совершает работу большую, чем полученная теплота, тогда его температура понижается, несмотря на приток теплоты. Теплоёмкость в этом случае отрицательна. В общем случае .