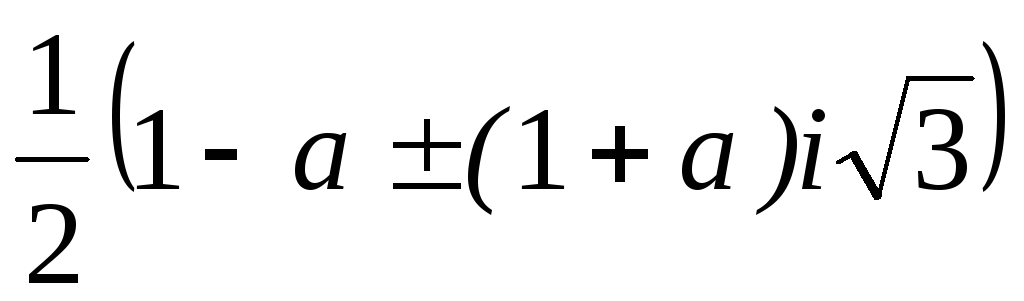- •А л г е б р а
- •Глава 1. Системы линейных уравнений и арифметическое векторное пространство. §1. Системы линейных уравнений и их решение методом Гаусса.
- •§2. Арифметическоеn-мерное векторное пространство. Линейная зависимость и независимость. Базис и ранг системы векторов.
- •§3. Однородная система линейных уравнений. Фундаментальный набор решений.
- •Глава 2. Матрицы и определители. §4. Алгебра матриц.
- •§5. Определитель квадратной матрицы.
- •Глава 3. Комплексные числа. §6. Поле комплексных чисел.
- •§7. Уравнения третьей степени.
- •§8. Уравнения четвёртой степени.
- •Литература.
- •На молдавском языке.
§7. Уравнения третьей степени.
Уравнение третьей
степени
x3+ax2+bx+c=0 (1)
подстановкойx=y–![]() приводится кприведенному кубическому
уравнению
y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=
приводится кприведенному кубическому
уравнению
y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v= , (3)
гдеu=
, (3)
гдеu= ,v=
,v= и
они связаны соотношениемuv=
и
они связаны соотношениемuv=![]() . (4)
С
учётом (4) формулу Кардано (3) можно
использовать и в таком виде:y=u
. (4)
С
учётом (4) формулу Кардано (3) можно
использовать и в таком виде:y=u![]() ,
гдеu=
,
гдеu= . (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
. (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
Чтобы не запоминать
формулу, можно пользоваться методом
решения, по сути повторяющим вывод
формул Кардано. Чтобы найти корни
уравнения (2) (считаем р0),
пологаяy=u+v,
подставляем его в уравнение:
(u+v)3+p(u+v)+q=0.
Раскрыв
скобки, и перегруппировав члены,
получим:
(u3+v3+q)+(
3uv+p)(u+v)=0.
Для
уничтожения второго слагаемого подберёмu, vтак, чтобы 3uv+p=0
илиuv=![]() .
Тогда уравнение (2) приводится к системе
уравнений:
.
Тогда уравнение (2) приводится к системе
уравнений:![]()
![]()
 Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz
Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz![]() =0.
=0.
Затем, выбираем
один (любой) корень z1этого квадратного уравнения. Берём
в качествеu1одно (любое) значение кубического корня
изz1и вычисляем
корни кубического уравнения (1) по
следующей схеме:
u1,
v1=![]() ,y1=u1+v1,x1=y1–
,y1=u1+v1,x1=y1–![]() ;u2=
u11,
v2=
v12,y2=u2+v2,x2=y2–
;u2=
u11,
v2=
v12,y2=u2+v2,x2=y2–![]() ;u3=
u12,
v3=
v11,y3=u3+v3,x3=y3–
;u3=
u12,
v3=
v11,y3=u3+v3,x3=y3–![]() ;
где1,2=
;
где1,2=![]() невещественные кубические корни из
единицы. Заметим, что2=(1)2=
невещественные кубические корни из
единицы. Заметим, что2=(1)2=![]() и1=(2)2=
и1=(2)2=![]() ,
это позволяет варьировать нахождениеu2, v2,
u3, v3.
,
это позволяет варьировать нахождениеu2, v2,
u3, v3.
При исследовании уравнений третьей степени используют теорему:
Теорема. Пустьx3+px+q=0
неполное кубическое уравнение с
действительными коэффициентами.
Обозначим
∆=![]() .
.
Если ∆>0, то уравнение имеет один действительный и два мнимых сопряжённых корня.
Если ∆=0, то корни уравнения действительны и хотя бы один из них кратный.
Если ∆<0, то все корни действительны и различны.
Если не все
коэффициенты уравнения (2) действительны,
то для упрощения вычислений можно
вычислить ∆. Если ∆=0 (p0,q0),
тогда уравнение (2) имеет два равных
корняy2=y3,
и в этом случае корни уравнения (2)
можно найти, не прибегая к извлечению
корней второй и третьей степени, а
именноy1=![]() ; y2=y3=
; y2=y3=![]() . (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
. (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
Пример 1. Решить уравнение:
x3–6x+9=0.
Решение.Уравнение
приведенное (отсутствует член сx2).
Используем модифицированную формулу
Кардано (5):
∆=![]() =
=![]() =
=![]() >0.
>0.![]() (берём
только одно значение квадратного
корня). Тогдаu=
(берём
только одно значение квадратного
корня). Тогдаu=![]() .
Одно
из значений
.
Одно
из значений![]() естьu1=–1, ещё
два значения получим, умножаяu1на1,2
– кубические корни из единицы. Итак,
u1=–1
,
x1=
u1–
естьu1=–1, ещё
два значения получим, умножаяu1на1,2
– кубические корни из единицы. Итак,
u1=–1
,
x1=
u1–![]() =–1–
=–1–![]() =–3;
u2=
u11=–1,
x2=
u2–
=–3;
u2=
u11=–1,
x2=
u2–![]() =–1+
=–1+![]() =–1–2/1=
=–1–22=
=–1–2/1=
=–1–22=![]() .
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=
.
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=![]() (x3не нужно
вычислять по формуле).
(x3не нужно
вычислять по формуле).
Ответ:x1=–3,
x2,3=![]() .
.
Пример 2. Решить уравнение:x3+9x2+18x+28=0.
Решение.
Сделаем подстановкуx=y–![]() =y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v:
(u+v)3–9(u+v)+28=0,
(u3+v3+28)+(3uv–9)(u+v)=0.
Откуда
=y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v:
(u+v)3–9(u+v)+28=0,
(u3+v3+28)+(3uv–9)(u+v)=0.
Откуда![]() ,
или
,
или![]() ,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
Один из корней
последнего уравнения z1=–1,
тогдаu1=–1,
v1=![]() =–3,y1=–4,x1=–7;u2=
u11=
=–3,y1=–4,x1=–7;u2=
u11=![]() ,v2=
v12=
,v2=
v12=![]() ,y2=
,y2=![]() ,x2=
,x2=![]() ;
Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=
;
Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=![]() .
.
Ответ: x1=–7,
x2,3=![]() .
.
Пример 3. Решить уравнение:x3+3x–2i=0.
Решение. Данное
уравнение приведенное, и не все его
коэффициенты действительны, поэтому
вычислим ∆.
∆=![]() =
=![]() =–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1=
=–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1=![]() =
=![]() ; x2=x3=
; x2=x3=![]() =
=![]() .
.
Ответ: x1=–2i, x2,3=i.
Пример 4. Решить уравнение:x3–3abx+ a3+b3=0
Решение.
Пологаяx=u+v,
получим
(u+v)3–3ab(u+v)+
a3+b3=0
или (u3+v3+
a3+b3)+(3uv–3ab)(u+v)=0.
Откуда![]() Одно
из решений последней системы
Одно
из решений последней системы
Тогда
u1=–a,
v1=–b,
x1=–a–b;
u2=
u11=![]() ,
v2=
v12=
,
v2=
v12=![]() ,
x2=
,
x2=![]() .
.
Ответ:
x1=–a–b,
x2,3=![]() .
.
Замечание: При выписывании ответа воспользовались тем, что при вещественныхa,bне надо вычислять x3. Но если выписанное значениеx3есть корень уравнения при (любых) вещественныхa иb, то ясно, чтоx3 будет корнем при любыхa,b.
Для самостоятельного решения.
Решить уравнения:
x3+6x2–12x+32=0
x3+9x2–18x+44=0
x3–3x2–6x+36=0
x3–12x2+24x–40=0
x3–6ix+4(1–i)=0
x3+(3–3i
 )x–9=0
)x–9=0x3+3ax+1–a3=0
Ответы:
(–8;
 )
)(–11;
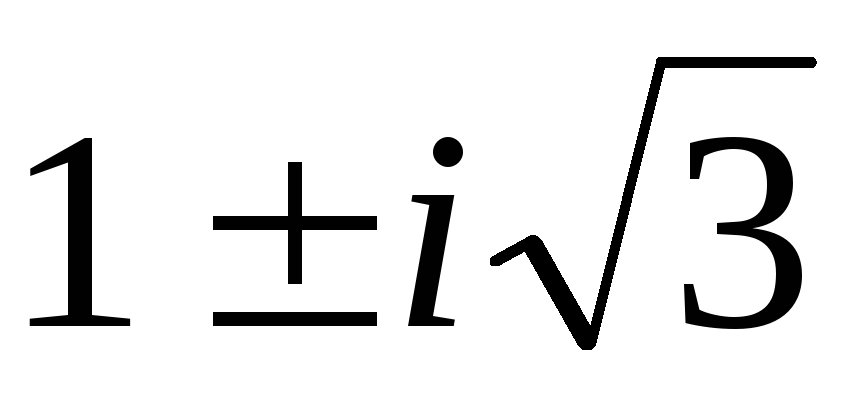 )
)(–3;
 )
)(10;
 )
)(2+2i; –1–i; –1–i)
(i
 ;
;


(a–1;