ФВТ (КХТП) / Методы оптимизации / Оптимизация - Лекции - Дудоров - 2004 / Лекция 6

4

Лекция 6

Решение систем нелинейных алгебраических уравнений

Классификация методов решения систем нелинейных алгебраических уравнений

Итерационные:

1. Метод простых итераций;

2. Метод поочерёдного изменения переменных.

Градиентные:

1. Метод Ньютона-Рафсона;

2. Метод наискорейшего спуска.

Итерационные методы решения систем нелинейных алгебраических уравнений

Метод простых итераций по сути своей аналогичен соответствующему методу решения систем линейных алгебраических уравнений. Для исходной системы уравнений вида f_i(x)=0, где i – индекс уравнения в системе, можно составить итерационную форму, при которой каждое уравнение системы будет выглядеть следующим образом:

. (1)

На каждом шаге итерации (k) ведётся пересчёт значений переменных по схеме .

Условием окончания выполнения процедуры является выполнение следующего нестрогого неравенства:

, (2)

где m – количество уравнений в системе (количество переменных),  – заданная точность решения.

Сходимость метода считается хорошей, если функциональная зависимость величины от шага итерации k является монотонно убывающей.

Задание 1. Найти графически, с точностью до целого числа, приближённое решение системы нелинейных алгебраических уравнений (СНАУ):

Полученное решение использовать для уточнения корня уравнения с точностью до 0,001 методом простых итераций.

Решение. Для нахождения приближённых значений решения системы уравнений графическим методом преобразуем заданную систему уравнений следующим образом:

Построим графики уравнений преобразованной системы уравнений в системе координат x₁-x₂ (рис. 1).

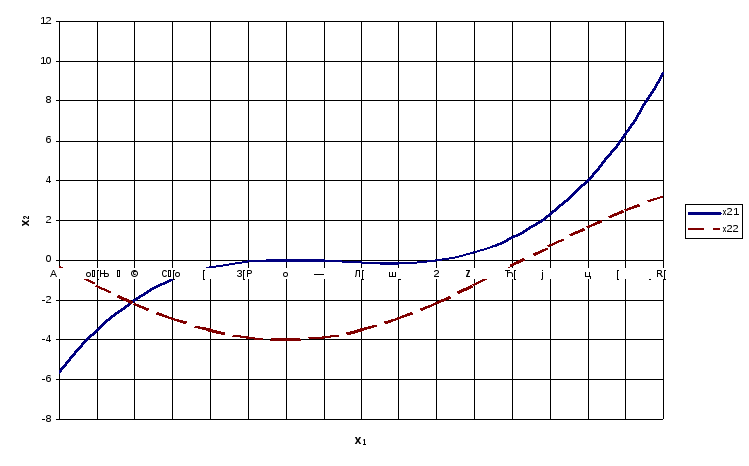
Рис. 1. Графическое решение системы уравнений.

Координаты точки пересечения графиков функций являются решением заданной СНАУ. При требуемой точности этим решением является пара координат (–1, –2).

Для уточнения корней методом простых итераций приведём заданную систему уравнений к итерационной форме:

В результате решения системы в итерационной форме имеем уточнённые значения корней: x₁=–1,019; x₂=–2,096.

Возможные проблемы решения СНАУ методом простых итераций связаны с преобразованием исходных функций к итерационной форме и выбором начального приближения.

Другой метод решения СНАУ заключается в поочерёдном изменении переменных с целью минимизации целевой функции. Алгоритм данного метода заключается в следующем.

1. Для заданной системы нелинейных алгебраических уравнений:

задаётся начальное приближение .

2. Изменяя значение переменной x₁, находим такое, которое обеспечит минимум функции:

. (3)

3. Процедуру, указанную в п. 2, повторяем последовательно для всех остальных переменных.

4. Цикл по всем переменным с шага 2 повторяется до тех пор, пока не будет обеспечена заданная точность  (2).

Градиентные методы решения систем нелинейных алгебраических уравнений

Градиентные методы решения СНАУ по сути своей тоже итерационные. Главное их отличие от предыдущих заключается в том, что для определения направления поиска решения используются частные производные.

Итерационная формула метода Ньютона-Рафсона имеет вид:

, (4)

где  – параметр, влияющий на скорость решения системы методом Ньютона-Рафсона.

Условие окончание итерационной процедуры аналогично предыдущим случаям.

Задание 2. Решить СНАУ методом Ньютона-Рафсона с точностью 0,001 при начальном приближении (1; /2):

Матрица частных производных имеет вид:

.

С учётом начального приближения, матрица имеет вид .

Получим обратную матрицу: .

Примем =1.

Теперь окончательный вид итерационной формы системы уравнений будет следующим:

.

Искомый результат достигается в несколько раз быстрее, чем в случае метода простых итераций.

В более общем случае обращённая матрица частных производных пересчитывается на каждом шаге итерации. Это увеличивает объём вычислений для каждого шага итерации, однако уменьшает само число итераций.

Итерационная формула метода наискорейшего спуска (градиента) имеет вид:

, (5)

где функция F имеет вид (3).

Значения  рассчитываются из условия минимизации функции:

.