2. Решение экономических задач с помощью надстроек ms Excel

Широкое применение на практике находят функции и режимы Excel, предназначенные для поиска решений уравнений и решения оптимизационных задач. Так, например, надстройка "Подбор параметра" реализует алгоритм численного решения уравнения, зависящего от одной или нескольких переменных.

Решение с помощью этого метода разделяется на два этапа:

1. сначала необходимо задать на рабочем листе ячейки, которые содержат переменные решаемого уравнения, т.е. задать влияющие ячейки, а затем задать ячейки с формулами решаемого уравнения, т.е. зависимые или целевые ячейки.

2. затем ввести адреса влияющих и целевой ячеек в диалоговое окно "Подбор параметра" и получить ответ, либо получить сообщение об отсутствии ответа, т.е. невозможности его найти.

Пример применения надстройки "Подбор параметра".

Определить, при какой ежемесячной процентной ставке можно за год накопить 5 тыс.руб., внося каждый месяц платеж на 10 % больше предыдущего, начав с платежа 100 руб.

Эту задачу нельзя решить лишь с помощью одной финансовой функции, т.к. в ней слишком много неизвестных. Для решения сначала необходимо смоделировать поток реальных платежей (рис. 2).

Рис. 2. Моделирование потока платежей

Затем, используя функцию БС (будущая стоимость инвестиций), можно найти накопленную к концу года сумму, нарастив каждый платеж по предполагаемой ставке (12%) на соответствующее число процентных периодов, а именно первый платеж на 12 месяцев вперед, второй - на 11 и т.п. (рис. 3).

Рис. 3. Расчет накопленной к концу года суммы по предполагаемой ставке

Далее с помощью надстройки "Подбор параметра" можно найти истинное значение процентной ставки. Для этого необходимо запустить эту надстройку, через меню "Сервис", а затем в открывшемся диалоговом окне установить необходимые значения, нажать клавишу "Ок" (рис. 4).

Рис. 4. Подбор параметра

В результате, получен ответ: ежемесячная процентная ставка составит 14,86% (рис. 5).

Рис. 5. Результат подбора параметра

Значительно более мощным по сравнению с Подбором параметра средством решения уравнения, а также достаточно эффективным инструментом решения задач линейного программирования (ЗЛП) является программная надстройка "Поиск решения".

ЗЛП – называются задачи, у которых линейны, во-первых, условия функции, а во-вторых, уравнения и неравенства определены ограничениями и условиями.

Если эта надстройка не установлена, то её нужно установить, как было описано выше, а если же она установлена, то для её запуска необходимо выполнить в меню "Сервис" команду "Поиск решения". После этого появиться диалоговое окно Поиск решения. В этом окне есть три основных параметра (рис. 6):

• Установить целевую ячейку;

• Изменяя ячейки;

• Ограничения.

Рис. 6. Поиск решения

Сначала нужно заполнить поле "Установить целевую ячейку". Поэтому во всех задачах для средства "Поиск решения" оптимизируется результат одной из ячеек рабочего листа. И эта целевая ячейка связывается с другими ячейками этого рабочего листа с помощью формул.

Средство "Поиск решения" использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск как наименьшего, так и наибольшего значения для целевой ячейки или установить конкретное значение. Таким образом, задается направление целевой функции.

Второй параметр средства "Поиск решения" – это параметр "Изменяя ячейки". В этом параметре указываются ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. К этим ячейкам предъявляются два основных требования: они не должны содержать формул и изменение их значений должно отражаться на изменении результата в целевой ячейке. Т.е. целевая ячейка зависит от изменяемых ячеек.

Третий параметр, который вводится в окне "Поиск решения" – это "Ограничения".

Для примера будет рассмотрено решение одной из наиболее распространенных задач линейного программирования – транспортной задачи с помощью надстройки "Поиск решения".

Пример решения транспортной задачи

Постановка транспортной задачи. Некоторый однородный продукт, сосредоточенный у m поставщиков А_i в количестве a_i (i = 1,..., m) единиц, необходимо доставить n потребителям B_j в количестве b_j (j = 1, ... , n) единиц. Известна стоимость c_ij перевозки единицы груза от i-го поставщика к j-му потребителю. Составить план перевозок, позволяющий с минимальными затратами вывести все грузы и полностью удовлетворить потребителей.

Схематически условия задачи выглядят так:

Таблица 2

Исходные данные транспортной задачи

Мощности поставщиков	Мощности потребителей
	250	100	150	50
80 320 100 50	6 8 5 9	6 30 4 9	1 6 3 9	4 5 30 9

Внутри данного прямоугольника заданы удельные транспортные затраты на перевозку единицы груза c_ij, слева указаны мощности поставщиков a_i, а сверху – мощности потребителей b_j.

Найти соответственно x_ij – найти соответственно оптимальный план закрепления поставщиков за потребителями.

Данная задача является закрытой, т.к. в ней суммарные запасы равны суммарным потребностям, т.е. сумма мощности поставщиков = сумме мощности потребителей = 550.

Ввод условий задачи в MS Excel состоит из нескольких шагов. Сначала необходимо создать форму для решения задачи, т.е. создать матрицу перевозок.

1. В блок ячеек В3:В6 ввести "1", тем самым зарезервировать место, где после решения задачи будет находиться распределение поставок.

2. Затем, необходимо ввести исходные данные, как в таблице 2. Причем, ввод мощностей поставщиков в ячейки А10:А13, потребности регионов в их продукции в ячейки В9:Е9, а удельные затраты по доставке от поставщика к потребителю в ячейки В10:Е13 (рис. 7).

Рис. 7. Создание формы для ввода условий задачи

3. Затем, необходимо произвести ввод граничных условий. Т.е. ввести условия реализации мощностей поставщиков: В ячейку А3 ввести формулу: =СУММ(B3:E3).

4. Далее аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Для этого просто необходимо скопировать формулу из ячейки А3 в остальные ячейки.

5. Теперь необходимо ввести условия удовлетворения запросов потребителей. Для этого в ячейку В7 необходимо ввести формулу: =СУММ(B3:B6). Аналогичные формулы необходимо ввести и в ячейки С7, D7 и Е7.

6. После этого необходимо назначить целевую функцию, т.е. функцию соответствующую минимальным затратам на доставку груза. Для этого необходимо зарезервировать ячейку и ввести в неё необходимую формулу. В ячейку В15 (целевая ячейка) установить курсор, далее с помощью "Мастера функций" выбрать функцию "СУММПРОИЗВ", нажать клавишу "Ок" и в открывшемся окне ввести необходимые данные:

• В поле Массив 1 указать адреса В10:Е13,

• В поле Массив 2 указать адреса В3:Е6, далее нажать клавишу "Ок".

После этого в поле ячейки В15 появится некоторое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (в данной задаче – это число 144).

Рис. 8. Введено выражение для вычисления значения целевой функции

7. Теперь нужно ввести зависимости из математической модели. Для этого необходимо запустить надстройку Поиск решения. В поле "Установить целевую ячейку" ввести адрес: $B$15, таким образом происходит резервирование целевой ячейки, куда после решения задачи будет помещено значение целевой функции.

8. Затем установить направление изменения целевой функции, равное Минимальному значению. В поле "Изменяя ячейки" ввести адреса $B$3:$E$6. Далее установить ограничения в поле "Ограничения", для этого щелкнуть клавишу "Добавить". В открывшемся окне "Добавление ограничения", в поле "Ссылка на ячейку" ввести адреса: $A$3:$A$6, в среднем поле выбрать знак "=", а в поле "Ограничения" вести адреса: $A$10:$A$13. подтвердить введенные ограничения, нажав клавишу "Ок". Аналогичным образом для ячеек с адресами: $B$7:$E$7 ввести ограничения: $B$9:$E$9.

9. После того, как введены все ограничения, необходимо щелкнуть клавишу "Параметры" и выбрать переключатель "Линейная модель" и переключатель "Неотрицательные значения". Далее нажать клавишу "Ок" и затем клавишу "Выполнить". После этого на экран сразу же выводится диалоговое окно "Результаты поиска решения" (рис. 9).

Рис. 9. Результаты поиска решения

В ходе решения данной задачи получен следующий план перевозок:

Таблица 3- План перевозок

Матрица перевозок (изменяя ячейки)
80 320 100 50	0 200 0 50	0 0 100 0	80 70 0 0	0 50 0 0
550	250	100	150	50

Этот план означает, что:

Х₁₃ = 80 ед.груза следует перевезти от поставщика 1 к потребителю 3;

Х₂₁ = 200 ед.груза следует перевезти от поставщика 2 к потребителю 1;

Х₂₃ = 70 ед.груза следует перевезти от поставщика 2 к потребителю 3;

Х₂₄ = 50 ед.груза следует перевезти от поставщика 2 к потребителю 4;

Х₃₂ = 100 ед.груза следует перевезти от поставщика 3 к потребителю 2;

Х₄₁ = 50 ед.груза следует перевезти от поставщика 4 к потребителю 1;

Общая стоимость перевозок = 3200.

Пример решения задачи анализа

Ещё одной немало важной надстройкой является надстройка "Анализ данных", которая также находит своё применение на практике.

Например, данная надстройка используется для моделирования временных рядов. "Пакет анализа" - обеспечивает дополнительные возможности анализа набора данных. Выбор конкретного метода анализа осуществляется в диалоговом окне.

Для применения данной надстройки будет рассмотрен способ проверки временного ряда на наличие тренда.

Один из способов проверки обнаружения тренда основан на сравнении средних уровней ряда: временной ряд разбивают на две примерно равные по числу уровней части, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность, имеющая нормальное распределение.

Если временной ряд имеет тенденцию к тренду, то средние, вычисленные для каждой совокупности, должны существенно различаться между собой. Если же расхождение незначительно, несущественно, то временной ряд не имеет тенденции.

Таким образом, проверка наличия тренда в исследуемом ряду сводится к проверке гипотезы о равенстве средних двух нормально распределенных совокупностей. Среднее значение можно трактовать как своеобразную середину области возможных значений случайной величины. Важно знать, как сильно значение изучаемой величины отличается от её среднего значения. Разброс и рассеивание случайной величины характеризует параметр, который называется дисперсией. Т.е. дисперсия характеризует степень отклонения возможного значения случайной величины относительно среднего.

Так, необходимо определить наличие основной тенденции (тренда) по данным таблицы 4.

Таблица 4

Урожайность пшеницы в одной из областей Среднего Поволжья, ц/га

Годы	1	2	3	4	5	6	7
Урожайность	14,1	9,3	19,4	19,7	5,4	24,2	13,8
Годы	9	10	11	12	13	14	15
урожайность	14,7	16,6	5,6	16,2	25,3	11,9	18,5

Итак, для того, чтобы определить наличие основной тенденции по данным, указанным в таблице 4, нужно проверить гипотезу о равенстве (однородности) дисперсий обеих частей данного временного ряда. Такую проверку можно выполнить с помощью F-критерия Фишера. В MS Excel же это можно сделать с помощью F-теста, который можно найти среди инструментов Анализа данных.

Сначала для этого необходимо ввести данные на рабочем листе MS Excel, затем вызвать надстройку Анализ данных известным ранее способом, из доступных инструментов анализа выбрать Двухвыборочный F-тест для дисперсии. В открывшемся окне ввести данных для этого анализа (рис. 10).

Рис. 10. Ввод данных для двухвыборочного F-теста

Далее необходимо нажать клавишу "Ок" и результат выполнения этого теста будет получен (рис. 11).

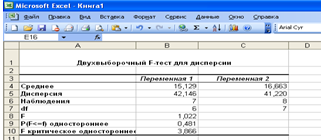
Рис. 11. Результат выполнения двухвыборочного F-теста для дисперсии

Отсюда можно сделать выводы, что дисперсия различается несущественно, т.к. F-критерий расчетный меньше, чем F-критический. Т.к. 1,022 <3,866.

Чтобы окончательно убедиться, можно проверить основную гипотезу о равенстве средних значений с помощью t-критерия Стъюдента.

Для этого нужно выбрать инструмент анализа Двухвыборочный t-тест с одинаковыми дисперсиями, ввести исходные данные (рис. 12).

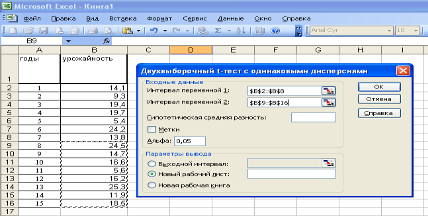
Рис. 12. Ввод данных для двухвыборочного t-теста с одинаковыми дисперсиями

После нажатия на клавишу "Ок", также будет получен результат выполняемого анализа (рис. 13).

Рис. 13. Результат выполнения t-теста

Анализируя полученные результаты, можно сказать, что нет оснований отвергать нулевую гипотезу о равенстве средних, расхождения между ними незначимы. Т.к. t-критерий расчетный по модулю меньше, чем t-критический, т.е. |-0,46| < 2,16.

Отсюда вывод: тренд урожайности пшеницы отсутствует.

Таким образом, был проведен анализ временного ряда с помощью надстройки Анализ данных.