План лекции № 4
Решение дифференциальных уравнений параболического типа
1. Явная разностная схема
1.1. Характеристика явной разностной схемы
1.2. Метод решения явной разностной схемы
1.3. Алгоритм решения явной разностной схемы
2. Неявная разностная схема
2.1. Характеристика неявной разностной схемы
2.2. Вывод основных соотношений метода прогонки
2.3. Определение прогоночных коэффициентов на 1-м шаге по координате
2.4. Определение решения на правой границе
2.5. Метод прогонки – метод решения неявной разностной схемы
2.6. Алгоритм метода прогонки
3. Разностная схема Кранка-Николсона
3.1. Вывод разностной схемы Кранка-Николсона
3.2. Устойчивость разностной схемы Кранка-Николсона
3.3. Метод решения разностной схемы Кранка-Николсона
4. Разностная схема Саульева
4.1. Вывод разностной схемы Саульева
4.2. Определение порядка аппроксимации разностной схемы Саульева
4.3. Метод решения разностной схемы Саульева
4.4. Алгоритм решения разностной схемы Саульева
5. Сравнительная характеристика изученных разностных схем
6. Задания для самоконтроля
1. Явная разностная схема
1.1. Характеристика явной разностной схемы
Рассмотрим одномерное дифференциальное уравнение параболического типа с начальным и граничными условиями:
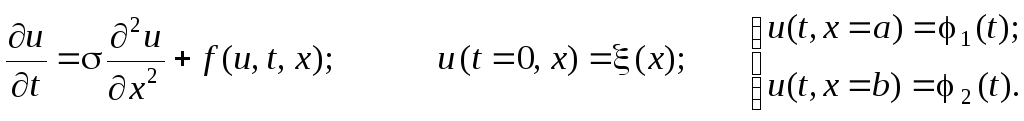(4.1)
Запишем для уравнения (4.1) явную разностную схему:
(4.2)
Запишем аппроксимацию начального и граничных условий:
(4.3)
Аппроксимация граничных условий (4.3) записана на (n + 1)-ом шаге по времени для удобства последующего изложения метода и алгоритма решения явной разностной схемы (4.2).
В разделе "Порядок аппроксимации разностной схемы" было доказано, что разностная схема (4.2) имеет порядок аппроксимации:
В разделе "Доказательство условной устойчивости явной разностной схемы" было получено условие устойчивости данной разностной схемы, накладывающее ограничение на выбор интервала деления при создании разностной сетки (или, иначе говоря, ограничение на выбор расчётного шага по одной из независимых переменных):
Отметим, что это, безусловно, является недостатком явной разностной схемы (4.2). В то же время она имеет достаточно простой метод решения.
1. Явная разностная схема
1.2. Метод решения явной разностной схемы
Выразим
из разностной схемы (4.2) величину
:
(4.4)
Значения
для любого j могут
быть определены с помощью аппроксимации
начального условия (4.3). Если задать n
= 0, то, пользуясь выражением (4.4), можно
определить значения
.
Значения
определяются с помощью аппроксимации
граничных условий (4.3). Далее, задаём n
= 1 и из выражения (4.4) определяем
,
а значения
– опять же с помощью аппроксимации
граничных условий (4.3) и т. д. Таким
образом, соотношение (4.4) позволяет
рассчитать все значения искомой функции
u в узлах разностной
сетки, кроме значений, задаваемых с
помощью начального и граничных условий.
Описанную методику решения явной
разностной схемы наглядно характеризует
её разностный шаблон (см. рисунок),
на котором n-й шаг по
времени следует считать известным, а
(n + 1)-й
шаг по времени – искомым.
Соотношения типа (4.4), позволяющие рассчитывать значения искомой функции u в узлах разностной сетки через известные значения функции u в других (как правило, соседних) узлах разностной сетки, называют рекуррентными соотношениями.
Обратим
внимание, что если вместо граничных
условий 1-го рода (4.1) будут заданы
граничные условия 2-го или 3-го рода, то
расчёт значений
несколько усложняется.
Рассмотрим граничные условия 2-го рода:
Запишем их аппроксимацию:
Выразим
значения
:
(4.4а)
Рассмотрим граничные условия 3-го рода:
Запишем их аппроксимацию:
Выразим
значения
:
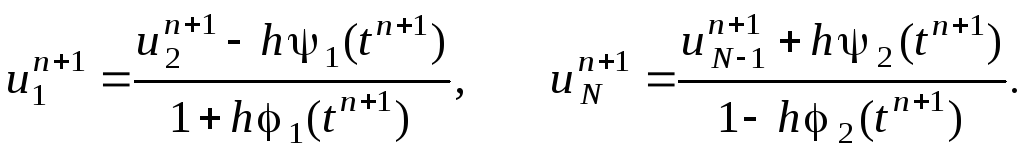(4.4б)
1. Явная разностная схема
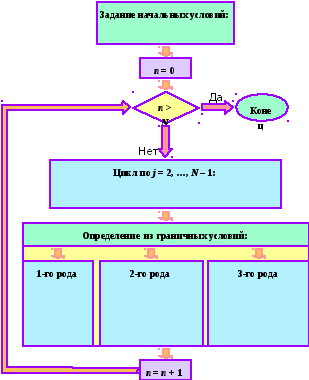
1.3. Алгоритм решения явной разностной схемы
Мы описали метод решения явной разностной схемы (4.2) для одномерного дифференциального уравнения параболического типа (4.1). Ниже приводится алгоритм решения, представленный для наглядности в виде блок-схемы.
2. Неявная разностная схема
2.1. Характеристика неявной разностной схемы
Рассмотрим одномерное дифференциальное уравнение параболического типа с начальным и граничными условиями:
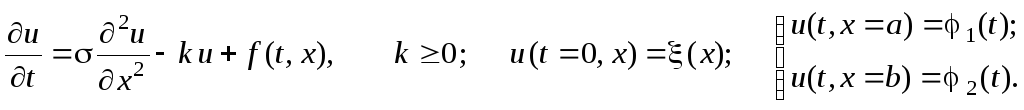(4.5)
Запишем для уравнения (4.5) неявную разностную схему:
(4.6)
Запишем аппроксимацию начального и граничных условий:
(4.7)
Аппроксимация граничных условий (4.7) записана на (n + 1)-ом шаге по времени для удобства последующего изложения метода и алгоритма решения неявной разностной схемы (4.6).
В разделе "Порядок аппроксимации разностной схемы" было отмечено, что разностная схема (4.6) имеет такой же порядок аппроксимации, как и соответствующая ей явная разностная схема (4.2), а именно:
В разделе "Доказательство абсолютной устойчивости неявной разностной схемы" было доказано, что неявная разностная схема (4.6) абсолютно устойчива, т.е. вне зависимости от выбора интервала деления на разностной сетке (или, иначе говоря, выбора расчётного шага по независимым переменным) погрешность решения неявной разностной схемы в процессе вычислений возрастать не будет. Отметим, что это, безусловно, является достоинством неявной разностной схемы (4.6) по сравнению с явной разностной схемой (4.2), которая устойчива только при выполнения условия (3.12). В то же время явная разностная схема имеет достаточно простой метод решения, а метод решения неявной разностной схемы (4.6), называемый методом прогонки, более сложен. Прежде чем перейти к изложению метода прогонки, необходимо вывести ряд соотношений, используемых этим методом.