Реферат
По дисциплине: Методы оптимизации
На тему: Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
Фаттахов Р.Р.
-
Классификация критериев оптимальности
-
Свойства выпуклых критериев оптимальности
-
Классификация детерминированных задач оптимизации.
-
Классификация критериев оптимальности
Если
случайный вектор внешних параметров
![]() не
входит в критерий оптимальности
не
входит в критерий оптимальности
![]() (
(![]() ),
то этот критерий называется детерминированным
критерием оптимальности.
Если критерий оптимальности имеет вид
),
то этот критерий называется детерминированным
критерием оптимальности.
Если критерий оптимальности имеет вид
![]() (
(![]() ,
,![]() ),
где
),
где
![]() –
случайный вектор внешних параметров,
то этот критерий называется стохастическим
критерием оптимальности.
–
случайный вектор внешних параметров,
то этот критерий называется стохастическим
критерием оптимальности.
Прежде, чем говорить о классификации детерминированных критериев оптимальности, дадим определения некоторых свойств функций.
Вектор
![]() называется
точкой локального минимума функции
называется
точкой локального минимума функции
![]() (
(![]() ),
если для всех точек
),
если для всех точек
![]() ,
принадлежащих некоторой малой окрестности
,
принадлежащих некоторой малой окрестности
![]() (
(![]() )
точки
)
точки
![]() имеем
имеем
![]() (
(![]() )
)![]() (
(![]() ),
),
![]() (
(![]() )
)![]() .
.
Значение
функции
![]() (
(![]() )
в точке локального минимума называется
локальным минимумом функции
)
в точке локального минимума называется
локальным минимумом функции
![]() (
(![]() ).
Таким образом, если точка
).
Таким образом, если точка
![]() является
точкой локального минимума функции
является
точкой локального минимума функции
![]() (
(![]() ),
то величина
),
то величина
![]() (
(![]() )
есть локальный минимум этой функции.
)
есть локальный минимум этой функции.
Точка
![]() называется
точкой глобального минимума функции
называется
точкой глобального минимума функции
![]() (
(![]() ),
если
),
если
![]() (
(![]() )
)![]() (
(![]() ),
),
![]()
таким
образом, точка наименьшего из всех
локальных минимумов называется точкой
глобального минимума функции
![]() (
(![]() ).
Соответствующее значение функции
).
Соответствующее значение функции
![]() (
(![]() )
называется глобальным минимумом этой
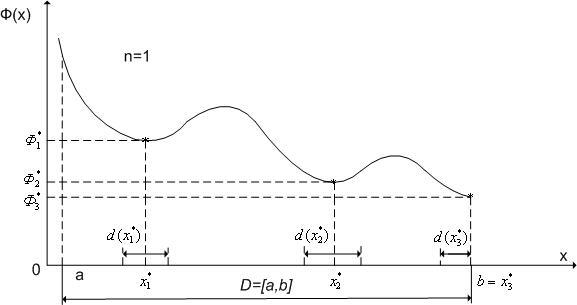
функции Например, на рис. 1, который
иллюстрирует одномерный случай
)
называется глобальным минимумом этой
функции Например, на рис. 1, который
иллюстрирует одномерный случай
![]()
![]() ,
,![]() ,
,![]() -точки
локального минимума функции
-точки
локального минимума функции
![]() (
(![]() ),
а величины Ф1*,Ф2*,Ф3*-
соответствующие локальные минимумы
этой функции,
),
а величины Ф1*,Ф2*,Ф3*-
соответствующие локальные минимумы
этой функции,
![]() -
точка глобального минимума функции
-
точка глобального минимума функции
![]() (
(![]() ),
а Ф3*-
глобальный минимум этой функции.
),
а Ф3*-
глобальный минимум этой функции.
|
|
Рис. 1. К определению локального и глобального минимумов функции
Критерий
оптимальности
![]() (
(![]() ),
где
),
где
![]() [
[![]() ,
,![]() ]
скаляр, называется унимодальным
критерием оптимальности,
если в области определения [
]
скаляр, называется унимодальным
критерием оптимальности,
если в области определения [![]() ,
,![]() ]
функции
]
функции
![]() (
(![]() )
существует точка
)
существует точка
![]() [
[![]() ,
,![]() ]
такая, что на полуинтервале [
]
такая, что на полуинтервале [![]() ,
,![]() )
функция
)
функция
![]() (
(![]() )
убывает, а на полуинтервале (
)
убывает, а на полуинтервале (![]() ,
,![]() ]-возрастает.
Заметим, что определение одномерного
унимодального критерия оптимальности
не требует непрерывности функции
]-возрастает.
Заметим, что определение одномерного
унимодального критерия оптимальности
не требует непрерывности функции
![]() (
(![]() ).
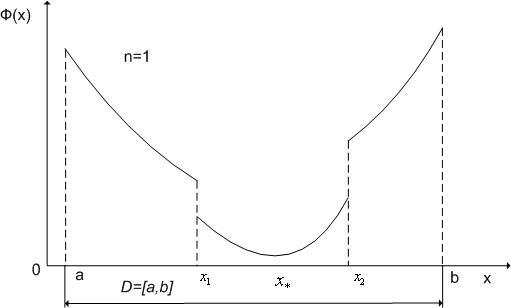
Например, на рис. 2 одномерная функция
).
Например, на рис. 2 одномерная функция
![]() на
интервале
на
интервале
![]() является
унимодальной, хотя и имеет в точках
является
унимодальной, хотя и имеет в точках
![]() ,
,
![]() разрывы.
Заметим также, что точка
разрывы.
Заметим также, что точка
![]() может
быть как внутренней точкой отрезка
[
может
быть как внутренней точкой отрезка
[![]() ,
,![]() ],
так и совпадать с одним из его концов.
],
так и совпадать с одним из его концов.
|
|
Рис. 2. К определению унимодального критерия оптимальности: x1,x2 - точки разрыва критерия оптимальности Ф(x).
Непрерывный
в своей области определения одномерный
критерий оптимальности
![]() ,
,
![]() называется
выпуклым
критерием оптимальности
(выпуклым вниз критерием оптимальности),
если для любых точек
называется
выпуклым
критерием оптимальности
(выпуклым вниз критерием оптимальности),
если для любых точек
![]() ,
,
![]() выполняется
неравенство
выполняется
неравенство
![]()
где
произвольное число
![]() .
.
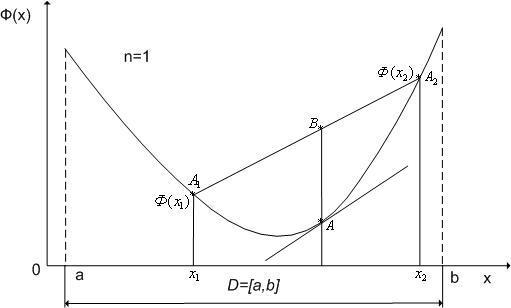
Приведенное
определение имеет простой геометрический
смысл: если критерий оптимальности
![]() (
(![]() )
выпукл на интервале [
)
выпукл на интервале [![]() ,
,![]() ],
то все точки любой дуги его графика
лежат под соответствующей хордой (см.
рис. 3).
],
то все точки любой дуги его графика
лежат под соответствующей хордой (см.
рис. 3).
|
|
Рис. 3. К определению выпуклого одномерного критерия оптимальности.
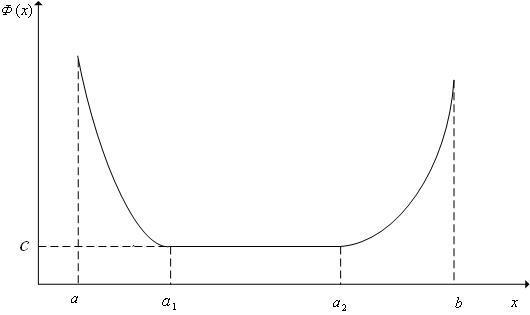
Заметим, что определение выпуклого критерия оптимальности не требует его унимодальности. Так что, например, выпуклым является критерий оптимальности, график которого изображен на рис. 4.
|
|
Рис. 4. Пример выпуклого критерия оптимальности: на интервале [a1,a2] значения критерия оптимальности постоянны и равны c.
Непрерывный
в своей области определения одномерный
критерий оптимальности
![]() (
(![]() ),
),
![]() [
[![]() ,
,![]() ]
называется строго
выпуклым критерием оптимальности
(строго
выпуклым вниз критерием оптимальности),
если для любых точек
]
называется строго
выпуклым критерием оптимальности
(строго
выпуклым вниз критерием оптимальности),
если для любых точек
![]() ,
,![]() [
[![]() ,
,![]() ],
],
![]() выполняется
неравенство
выполняется
неравенство
![]() (
(![]() +(1-
+(1-![]() )
)![]() )<
)<![]() (
(![]() )+(1-
)+(1-![]() )
)![]() (
(![]() ),
),
где
произвольное число
![]() [0,1].
[0,1].
Строго вогнутый критерий является унимодальным критерием.
Если
множество
![]() является
выпуклым множеством, то в многомерном
случае
является
выпуклым множеством, то в многомерном
случае
![]() 2
также определено понятие выпуклого
критерием оптимальности.
2
также определено понятие выпуклого
критерием оптимальности.
Непрерывный
критерий оптимальности
![]() (
(![]() ,
где
,
где
![]() и
множество
и
множество
![]() является
выпуклым множеством, называется выпуклым
критерием оптимальности (выпуклым вниз
критерием оптимальности), если для любых
является
выпуклым множеством, называется выпуклым
критерием оптимальности (выпуклым вниз
критерием оптимальности), если для любых
![]() ,
,![]() ,
,
![]() и
любого
и
любого
![]() [0,1]
выполняется неравенство
[0,1]
выполняется неравенство
![]()
Аналогично,
критерий оптимальности
![]() (
(![]() ,
где
,
где
![]() и
множество
и
множество
![]() является
выпуклым множеством, называется строго
выпуклым критерием оптимальности
(строго выпуклым вниз критерием
оптимальности), если для любых
является
выпуклым множеством, называется строго
выпуклым критерием оптимальности
(строго выпуклым вниз критерием
оптимальности), если для любых
![]() ,
,
![]() и
любого
и
любого
![]() выполняется
неравенство
выполняется
неравенство
![]()
Отметим, что выпуклая функция может иметь более одной точки локального минимума (см. Пример 1.4.1), а строго выпуклая функция – только одну точку.
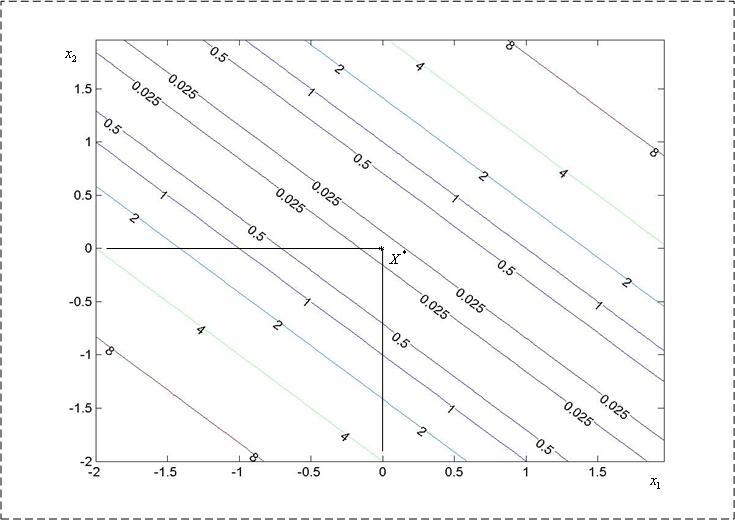
Пример 1
Рассмотрим
выпуклую квадратичную функцию
![]() .
Легко видеть, что эта функция достигает
в точке (0,0) минимума, равного нулю. Но
это же значение функция принимает во
всех точках вида
.
Легко видеть, что эта функция достигает
в точке (0,0) минимума, равного нулю. Но
это же значение функция принимает во
всех точках вида
![]() -
см. рис. 5.
-
см. рис. 5.
|
|
Рис. 5. К прим. 1.
Заметим, что рис. 5 получен с помощью следующей MATLAB-программы:
x=-2:0.06:2;
y=x;
[X,Y]=meshgrid(x);
Z=(X+Y).^2;
V=[0.025,0.5,1,2,4,8];
[C,h]=contour(X,Y,Z,V);
clabel(C,h);
Критерий
оптимальности
![]() (
(![]() ),
имеющий в области определения несколько
локальных минимумов, называется
многоэкстремальным
критерим оптимальности
или мультимодальным критерием
оптимальности (см. прим. 2).
),
имеющий в области определения несколько
локальных минимумов, называется
многоэкстремальным
критерим оптимальности
или мультимодальным критерием
оптимальности (см. прим. 2).
Если
размерность вектора варьируемых
параметров
![]() больше
единицы (
больше
единицы (![]() >1),
то критерий оптимальности
>1),
то критерий оптимальности
![]() (
(![]() )
может быть в своей области допустимых
значений
)
может быть в своей области допустимых
значений
![]() "овражным"
критерием оптимальности.
Критерий оптимальности называется
овражным в своей области допустимых
значений, если в этой области имеют
место слабые изменения частных производных
функции
"овражным"
критерием оптимальности.
Критерий оптимальности называется
овражным в своей области допустимых
значений, если в этой области имеют
место слабые изменения частных производных
функции
![]() (
(![]() )
по одним направлениям и значительные
изменения этих производных по другим
направлениям (см. прим. 2).
)
по одним направлениям и значительные
изменения этих производных по другим
направлениям (см. прим. 2).
Пример 2
Рассмотрим
функцию Розенброка
![]() (
(![]() ,
,![]() )=100(
)=100(![]() -
-![]() )2+(1-
)2+(1-![]() )2
(
)2
(![]() =2).
Легко видеть, что минимум этой функции
достигается в точке (0,0) и равен нулю.
Линии уровня функции приведены на
рис. 6, который получен с помощью
следующей MATLAB-программы:
=2).
Легко видеть, что минимум этой функции
достигается в точке (0,0) и равен нулю.
Линии уровня функции приведены на
рис. 6, который получен с помощью
следующей MATLAB-программы:
x=-2:0.06:2;
y=x;
[X,Y]=meshgrid(x);
Z=100.*(Y-X.^2).^2+(1-X).^2;
V=[1,5,50,500];
contour(X,Y,Z,V);
|
|
Рис. 6. Линии уровня функции Розенброка. Функция медленно изменяется вдоль дна V-образного оврага и быстро – перпендикулярно этому дну.
Критерий
оптимальности
![]() (
(![]() )
называется сепарабельным
критерием оптимальности,
если функция
)
называется сепарабельным
критерием оптимальности,
если функция
![]() (
(![]() )
является сепарабельной, т.е. представляет
собой сумму функций, каждая из которых
зависит только от одной компоненты
вектора
)
является сепарабельной, т.е. представляет
собой сумму функций, каждая из которых
зависит только от одной компоненты
вектора
![]() :
:

Критерий
оптимальности
![]() (
(![]() )
называется позиномиальным
критерием оптимальности,
если функция
)
называется позиномиальным
критерием оптимальности,
если функция
![]() (
(![]() )
есть позином, т.е. если
)
есть позином, т.е. если
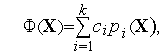
где
![]() и
все компоненты вектора
и
все компоненты вектора
![]() –
положительные действительные числа, а
функции
–
положительные действительные числа, а
функции
![]() (
(![]() )
имеют вид
)
имеют вид

![]() -
любые действительные числа.
-
любые действительные числа.