3.1. Составление схем включения приемников

а) Схема включения приемников «звезда с нулевым проводом»

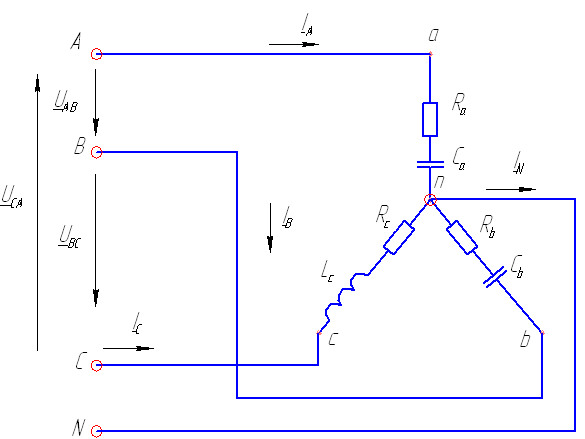
Рис.20.

б) Схема включения приемников «треугольник»

Рис.21.

3.2. Определение комплексов действующих значений фазных и линейных токов

а) Схема включения «звезда с нулевым проводом».

Рассчитаем фазное напряжение сети:

U_ф= = = 219,39 В.

Рассчитаем комплексы фазныхнапряжений:

Пусть, U_A=U_a=U_ф∙e= 219,39∙eВ

Из векторной диаграммы напряжений:

U_B= U_b =U_ф∙e= 219,39∙eВ

U_C= U_c =U_ф∙e= 219,39∙eВ

Рассчитаем сопротивления каждой фазы:

Z_a = R_a - j∙X_a = R_a - j∙ = 101 - j∙ = 101 - j∙36,606 =∙e= 107,429∙eОм

Z_b = R_b - j∙X_b = R_b - j∙ = 65 - j∙ = 65 - j∙34,244 =

= 73,469∙eВ

Z_с = R_с + j∙X_с = R_с + j∙= 73 + j∙2∙3,14∙50∙97∙10^-3 =73 + j∙30,458 =

= 79,099∙eВ

Определим комплексные токи в проводах сети:

I_A = = = 2,042∙e = 2,042∙(cos(19,922^°) + j∙sin(19,922^°)) = = 2,042∙( 1,903 + j∙0,69) = 1,903 + j∙0,69 А

I_B = = = 2,986∙e= -0,116 - j∙2,984 А

I_C = = = 2,774∙e= -0,364 + j∙2,75 А

Ток в нейтральном проводе:

I_N = I_A + I_B + I_C = 1,903 + j∙0,69 -0,116 - j∙2,984 -0,364 + j∙2,75 = 1,423 + j∙0,456 = = 1,494∙eА

б) Схема включения «треугольник»

Фазные напряжения равны линейным:

U_ф= U_Л = 380 В

Пусть, U_ab = U_AB = U_Л∙e= 380∙ e В

Из векторной диаграммы напряжений:

U_bс = U_BС = U_Л∙e= 380∙ e В

U_ca = U_CA = U_Л∙e= 380∙ eВ

Z_ab = Z_bc = Z_ca = R + j∙X_L = R + j∙(2πfL) = 108 + j∙(2∙3,14∙50∙76∙10^-3) = 108 + j∙23,864 = 110,605∙eОм

Находим фазные токи:

I_ab = = = 3,436∙e= 3,436∙(cos(17,54°) + j∙sin(17,54°)) = = 3,436∙(0,954 + j∙0,301) = 3,278 + j∙1,034 А

I_bc = = = 3,436∙e= -0,742 - j∙3,354 А

I_ca = = = 3,436∙e= -2,536 + j∙2,319 А

Рассчитаем линейныетоки по первому закону Кирхгофа:

I_A = I_ab - I_ca = 3,278 + j∙1,034 – (-2,536 + j∙2,319) = 5,814 - j∙1,285 =5,954∙eА

I_B = I_bc - I_ab = -0,742 - j∙3,354 – (3,278 + j∙1,034) = -4,02 - j∙4,388 =5,951∙e А

I_C = I_ca - I_bc = -2,536 + j∙2,319 – (-0,742 - j∙3,354) = -1,794 + j∙5,673 =5,95∙eА

3.3 Составление схем включений ваттметров для измерения активной мощности каждого трехфазного приемника

Рис.22(а)

Рис.22(б)

4. Расчет активных, реактивных и полных мощностей каждого приемника

а) Для схемы «звезда» с включением трехваттметров:

Активная мощность: P = P_a + P_b + P_c = I_A²∙R_a + I_B²∙R_b + I_C²∙R_c = (2,042)²∙101 + (2,986)²∙65 + (2,774)²∙73 = 1562,439 Вт

Реактивная мощность: Q = Q_a + Q_b + Q_c = - I_A²∙X_a - I_B²∙X_b + I_C²∙X_c = --

-+I_C²∙2∙π∙f∙L_c = - - + (2,774)²∙314∙97∙10^-3 = -

-152,638 – 305,328 + 234,377 = -223,589 Вар

Полная мощность: S = = = 1578,356 ВА.

б) Для схемы «треугольник» с включением двух ваттметров:

P₁=Re{S₁} =Re{U_AC∙I_A^*} =Re{(329,0896 -j∙190) ∙(5,814 +j∙1,285)}=Re{2157,477 -j∙681,78} = 2157,477 Вт

Q₁ = Im{ S₁ } = -681,78 Вар

Где U_AC= - U_CA= -380∙e= 329,0896 -j∙190

P₂=Re{S₂} =Re{U_BC∙I_B^*} =Re{- j∙380∙(-4,02 + j∙4,388)} = Re{1667,44 + j∙1527,6 } = 1667,44 Вт

Q₂ = Im{ S₂ } = 1527,6 Вар

Где U_BС = U_bс = 380∙ e= - j∙380 В

P = P₁ + P₂ = 2157,477 + 1667,44 = 3824,917 Вт

Q = Q₁ + Q₂ = -681,78 + 1527,6 = 845,82 Вар

S = = = 3917,32 ВА.

5. Построение векторных диаграмм токов и напряжений для каждого приемника

1. Несимметричная «звезда с нулевым проводом»(рис.23)

2. Симметричный « треугольник»(рис.24)

MI: 0,05 A : 1мм

MU: 2В : 1мм

Рис.23

MI: 0,1 A : 1мм

MU: 2В : 1мм

Рис.24