
Механика_сплошной_среды_
.PDF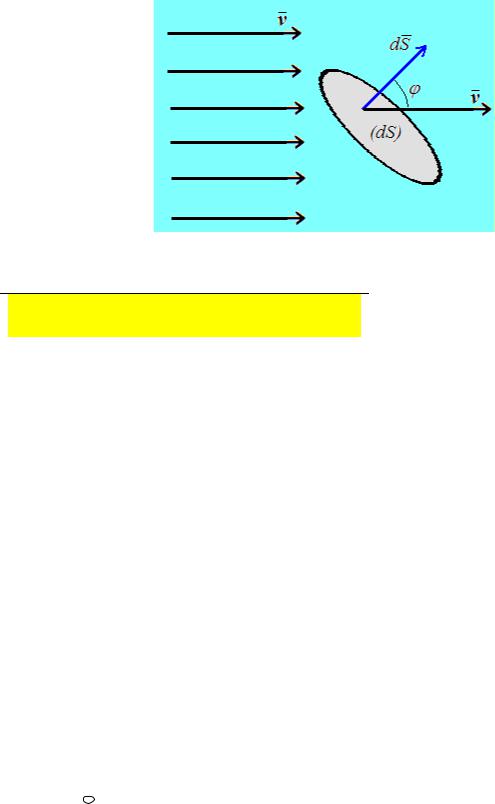
проницаемую для жидкости. На рис. 2.5 показан случай, когда
вектор dS площадки располагается под произвольным углом к
|
|
|
|
|
|
|
|
|
|
|
|
вектору скорости v. |
|
|
|
|
|
|
|
||||
Расход жидкости через площадку (dS ) будет равен |
|
|
|||||||||
|
|
(2.1) |
|
|
|
|
|
|
|||
dV v |
dS v dS cos . |
|
|
|
|
|
|
||||
Теперь в пространство, где |
|
|
|
|
|
|
|||||
течѐт жидкость или газ, по- |
|
|
|
|
|
|
|||||
местим |
произвольную |
по- |
|
|
|
|
|
|
|||
верхность (S ). Мысленно ра- |
|
|
|
|
|
|
|||||
зобьѐм (S ) на бесконечно ма- |
|
|
|
|
|
|
|||||
лые части. Расход сквозь ка- |
|
|
|
|
|
|
|||||
ждую часть определяется по |
|
|
|
|
|
|
|||||
формуле (2.1). Сложив (про- |
|
|
|
|
|
|
|||||
интегрировав) эти расходы, |
|
|
|
|
|
|
|||||
получим расход через всю (S) : |
|
Рис. 2.5 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
V v |
dS. |
|
|
|
|
(2.2) |
|
|
|
|
|
(S ) |
|
|
|
|
|
|
|
|
|
|
Расход жидкости (газа) через поверхность (S) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
(S ) |
|
Если |
сечение (S ) перпендикулярно |
скорости течения: |
|||||||||
v |
|||||||||||
(при этом 0) и скорость во всех точках (S ) одинакова, то из (2.2) |
|||||||||||
будем иметь |
V v S. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
(2.3) |
|||
Обыкновенно этой формулой пользуются при вычислении расхо-
да жидкости или газа через поперечное сечение трубопровода. |
|
|||
Умножим объѐм (2.1) на |
плотность . Получим массу жидкости, |
|||
протекающей сквозь (dS ) за единицу времени |
|
|||
|
|
|
|
(2.4) |
|
dm v |
dS. |
||
Проинтегрировав (2.4) по поверхности (S ), получим массу жидко- |
||||
сти, протекающей сквозь |
(S ) за |
единицу времени (массовый рас- |
||
ход): |
|
|
|
|
|
|
|
||
|
m v |
dS. |
|
|
|
( S ) |
|
|
|
Если поверхность (S ) замкнута, то по теореме о дивергенции |
||||
(П.4.2) это равенство равносильно такому: |
|
|||
|
|
|
|
|
m v |
dS div( v) dV |
(2.5) |
||
( S ) |
(V ) |
|
|
|
21
– масса жидкости, вытекающей из области (V ) за единицу време-
ни.
Пусть область (V ) мала; обозначим еѐ (dV ). Тогда из (2.5) полу-
чим |
|
|
|
|
|
|
|
|
|
|
dm |
|
|
|
|
|
(2.6) |
||||
div( v ) dV |
|
|||||||||
– масса жидкости, вытекающей из области |
(dV ) |
за единицу време- |
||||||||
ни. |
|
|
|
|
|
|
|
|
|
|
З а д а ч а 1. Дано поле скоростей текущей жидкости |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
(2z y2 )i ( y 4x) j 3zk . |
|
||||||||
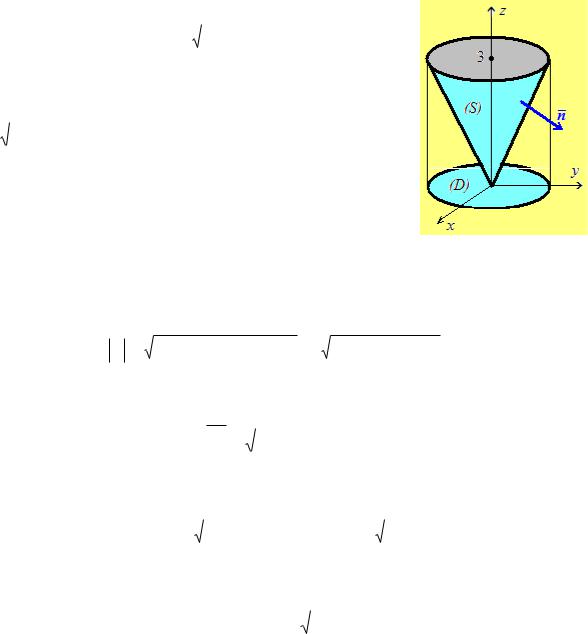
а) Найти расход через боковую поверхность |
конуса (S ), |
ограниченного задан- |
||||||||
ными поверхностями: |
|
|
|
|
|
|
|
|
|
|
z 3, |
|
|
|
|
|
|
|
|
(а) |
|
(S) : |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y |
2 |
|
|
|
|
||
z 2 |
|
x |
|
|
. |
|
|
|
||
б) Найти расход через всю поверхность конуса.
Начертим конус (рис. 2.6). Равенство z 3 есть урав-
нение |
горизонтальной |
плоскости. |
Равенство |
||
|
|
|
|
||
z 2 |
x2 y 2 есть уравнение конической поверхности. |
||||
а) Уравнение конической поверхности запишем так:
4x2 4 y 2 z 2 0.
(x, y,z)
Находим нормальный вектор
N ( 'x , 'y , 'z ) (8x, 8y, 2z).
После сокращения на +2 будем иметь N (4x, 4 y, При этом вектор укорачивается, но направление
Рис. 2.6
z).
не меняется. Его модуль
|
|
(4x)2 (4 y)2 ( z)2 |
|
16(x2 y 2 ) z 2 . |
N |
Единичный вектор, нормальный к боковой поверхности конуса, равен
|
|
|
|
|
|
(4x, 4 y, z) |
|
|
|
|
N |
|
|
|
|
||
n |
|
|
|
|
|
. |
||
|
|
|
|
|||||
|
|
|
N |
|
16(x 2 y 2 ) z 2 |
|
|
|
Находим скалярное произведение:
|
|
2 |
|
|
(4x, 4 y, z) |
|
|
4x(2z y 2 ) 4 y( y 4x) 3z 2 |
|||
v n |
(2z y |
|
, y 4x, 3z) |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
16(x 2 y 2 ) z 2 |
|
|
16(x 2 y 2 ) z 2 |
||||
Подставим в формулу расхода (2.2):
|
|
|
4x(2z y 2 ) 4 y( y 4x) 3z 2 |
||||
V v |
dS |
v |
n dS |
|
|
|
dS. |
|
|
|
|||||
|
|
||||||
(S ) |
|
(S ) |
(S ) |
16(x 2 y 2 ) z 2 |
|||
22

На поверхности конуса выполняется равенство z 2
 x2 y 2 . Подставим это значение:
x2 y 2 . Подставим это значение:
V |
4x(4 x2 y 2 |
y |
2 ) 4 y( y 4x) 12(x2 y 2 ) |
dD, |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
||||||||||||||||
(D) |
|
|
20(x2 y 2 ) |
|
|
|
|
|
|
|
|
|
||||||
где (D) круг, проекция боковой поверхности конуса (S) |
на плоскость Oxy. Из |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
2 |
y |
2 |
3, или |
|
2 |
|
2 |
|
|||||
системы уравнений (а) получим |
2 x |
|
|
x |
|
y |
|
|
|
|
|
окружность |
||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
радиуса 32 .
Для вычисления интеграла перейдѐм к полярной системе координат r, . Тогда
x r cos , |
y r sin , |
x 2 y 2 |
r 2 , |
|
dD rdrd и |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
(D) : |
0 2 , |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
r 3 / 2. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||
|
3 / 2 |
2 |
|
4r cos (4r r |
2 |
sin |
2 |
) 4r sin (r sin 4r cos ) 12r |
2 |
|
|||||||||||||||
V rdr d |
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
20r 2 |
|
|
|||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ввиду того, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||
cos d 0, |
sin 2 cos d 0, |
|
sin cos d 0, |
sin 2 d , |
|||||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
||
остаѐтся |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 / 2 |
4 r |
2 |
24 r |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
9 5 |
|
|
|
|
||||||||||||||||
|
|
|
V |
|
|
|
dr |
1.58. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
20 |
|
|
|
|
40 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отрицательность расхода означает, что жидкость в основном втекает через боковую поверхность конуса.
б) Вся поверхность конуса является замкнутой поверхностью, внутри которой находится весь конус (V ), поэтому можно воспользоваться формулой Остро-
градского-Гаусса. Но сначала найдѐм дивергенцию вектора скорости:
|
|
v |
|
v |
|
|
v |
3 |
(2z y 2 ) |
( y 4x) |
(3z) |
0 1 3 4. |
div v |
1 |
|
2 |
|
||||||||
|
|
x |
|
y |
|
z |
x |
y |
z |
|
||
|
|
|
|
|
|
|
|
|||||
По формуле расхода (2.2) имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V v |
dS |
[Применим формулу Остроградс кого |
Гаусса] div v dV |
|
||||||||||
(S ) |
|
|
|
|
|
|
|
(V ) |
|
|
|
|
|
|
|
|
4 dV 4 dV 4V 4 |
1 |
|
4 |
|
2 |
|
4 |
|
3 |
2 |
||
|
|
|
Sh |
|
r |
|
h |
|
|
|
|
3 9 . |
||
|
|
3 |
3 |
|
3 |
|
||||||||
|
|
(V ) |
(V ) |
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23

2.4. Расход при стационарном течении.
Течение называют стационарным, когда скорость не зависит от времени.
Рассмотрим течение жидкости в каком-либо трубопроводе через поперечные сечения (S1 ) и (S2 ) За единицу времени через сечение
(S1 ) втекает объѐм V1 v1S1, а через (S2 ) вытекает объѐм V2 v2S2 . Так как жидкость практически несжимаема, то в пространстве меж-
ду (S1 ) и (S2 ) объѐм жидкости не меняется. Значит, объѐм входящей жидкости через сечение (S1 ) равен объѐму выходящей жидкости че-
рез (S |
2 |
) : V |
V |
. Иначе говоря, V vS const . Таким образом, |
|
||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V vS const |
|
(2.7) |
|
|
|
|
|
Условие постоянства расхода |
|
|
Следовательно, там, где сечение больше, скорость меньше.
2.5. Одномерное течение. Уравнение Эйлера
Течение в одном направлении (вдоль определѐнной линии) назы-
вается одномерным.
В пространстве, где течѐт жидкость, выделим неподвижный бесконечно малый объѐм (dV ) в виде прямоугольного параллелепипеда
(рис. 2.4). Введѐм систему координат Oxyz. Обозначив размеры па-
раллелепипеда dx, dy, dz, получим |
|
dV dxdydz. |
(2.8) |
Масса жидкости внутри (dV ) равна |
|
dm dV , |
(2.9) |
где – плотность жидкости. Укажем силы, действующие на эту мас-
су (рис. 2.4).
24
Рис. 2.4
Наша цель – составить уравнение движения частиц жидкости. Для этого воспользуемся вторым законом Ньютона
|
|
dF |
dm a. |
Спроецируем векторы на ось Oy |
|
dF dm a.
Подставим (2.9): |
|
dF dV a. |
(2.10) |
Левая часть – суммарная сила, действующая на массу dm. Она равна
dF pdxdz w dV ( p y p)dxdz.
Так как y p py dy, то с учѐтом (2.8) это выражение можно упростить:
|
(2.11) |
dF (w py )dV. |
|
Подстановка (2.11) и (2.9) в (2.10) даѐт |
|
|
|
w py a, |
|
или |
|
w p a. |
(2.12) |
y |
|
Найдѐм ускорение a рассматриваемого элемента жидкости, находящегося внутри dV. Оно равно ускорению частиц, расположенных на левой грани параллелепипеда.
Обозначим v проекцию вектора скорости на ось Oy. Скорость частиц зависит от y и от t, поэтому
v v(t, y).
Отсюда следует, что |
|
|
|
|
(2.13) |
dv vt dt vy dy. |
||
Здесь dt время, за которое частицы, находящиеся на левой грани, пройдут расстояние dy. Тогда
|
|
dy vdt. |
|
|
|
(2.14) |
|
|
|
|
|
|
|
|
|
Подставим (2.14) в (2.13). Будем иметь dv (vt vvy )dt, отсюда |
|||||||
a |
dv |
vt vvy |
v |
v |
v . |
(2.15) |
|
dt |
t |
||||||
|
|
|
y |
|
|||
Осталось подставить (2. 15) в (2.12): 25
w |
p |
|
v |
v |
v |
|
|
|
. |
||
|
y |
|
t |
|
|
|
|
|
y |
Разделив обе части на , получим окончательно
v |
v |
v |
w |
1 |
|
p . |
|
|
|
|
|
|
|
||||
t |
|
y |
|
|
|
y |
|
(2.8) |
Уравнение Эйлера |
|
|
||||||
2.6. Уравнение Бернулли
Рассмотрим стационарное течение вдоль оси Oy. При стационар-
ном течении скорость со временем не меняется, поэтому v / t 0. Уравнение Эйлера (2.8) примет вид
v |
|
dv |
|
w |
1 |
|
dp |
. |
|
|
|
|
|
|
(а) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dy |
|
|
|
dy |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на ось Oy, наклонѐн- |
|
|
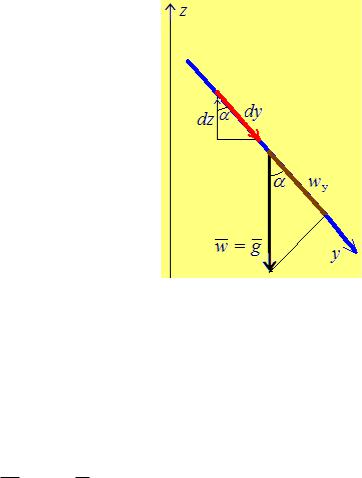
В поле силы тяжести w g. Спроецируем |
g |
|||||||||||||
ную под углом к вертикали Oz |
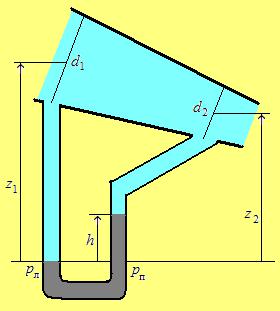
(рис. 2.5). Получим wy g cos . |
|||||||||||||||
Подставим в (а): |
|
|
|
|
|
|
|
|||||||||
v |
dv |
|
g cos |
1 |
|
dp |
, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
dy |
|
|
|
|
|
|
dy |
|
|
|
|
|||
|
vdv g cos dy |
dp |
0. |
|
(б) |
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
На рис. 2.5 видим, что когда координата y |
|
|||||||||||||
растѐт (dy 0), высота z уменьшается |
|
|
|
|||||||||||
(dz 0), |
поэтому cos |
dz |
. Подставим в (б): |
|
||||||||||
|
|
|
||||||||||||
|
|
|
|
dy |
|
|
|
|||||||
vdv gdz |
dp |
0, |
|
|
|
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||
|
vdv gdz |
dp |
0, |
|
|
Рис. 2.5 |
||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
v2 |
gz |
dp |
0. |
(2.9) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
||||||||||
У несжимаемой жидкости const. В этом случае равенство (2.9) запишется так:
v2 gz p C. 2
26
Умножив все члены на , получим
|
|
v 2 |
|
|
|
|
|
|
|
|
|
|
|
|
g z |
|
p |
|
const. |
|
(2.10) |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
Давление |
|
Статическо е |
|
|
|
|
|
|
Динамическ ое |
|
|
|
|
|
||||
|
положения |
|
давление |
|
|
|
|
|||
|
давление |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
Уравнение Бернулли |
|
|
|
|
|||
|
для несжимаемой и невязкой жидкости |
|
|
|||||||
З а д а ч а 1. В наклонном трубопроводе течѐт вода (рис. 2.6). В сечениях с диаметрами d1 0.25 м и d2 0.1 м производится замер давлений. Разница дав-
лений оказалась равной h 0.1м ртутного столба. Определить расход воды, если в 1000 кг/м3, рт 13600 кг/м3.
В обоих сечениях расход одинаков: V v1S1, V v2 S2 . Составим уравнение Бернулли для этих сечений:
|
|
v2 |
|
|
|
|
|
в |
v2 |
|
|
|
|
|
|
||||
|
|
в |
1 |
|
|
gz p |
|
|
2 |
|
|
gz |
|
p |
|
, |
|||
|
|
|
|
в |
|
|
|
|
в |
2 |
2 |
||||||||
|
|
2 |
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
p1 |
и |
p2 |
– статические |
|
давления в обоих сечениях, z1 и z2 – высоты до |
||||||||||||
обоих сечений, отсчитанные от общего горизонтального уровня (рис. 2.6). |
|||||||||||||||||||
Составим условие равенства давлений pл pп : |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
в gz1 p1 рт g h в g(z2 h) p2 . |
||||||
Решим систему уравнений: |
|
|
|
|
|||||||||||||||
V v S , |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
V v |
2 |
S |
2 |
, |
|
|
|
|
|
|
|
|
|
|
||
|
вv12 |
|
|
|
|
|
вv22 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
gz p |
|
|
gz |
|
p |
|
, |
|||||||
|
|
|
в |
2 |
2 |
|||||||||||
|
|
|||||||||||||||
2 |
|
|
|
|
в |
1 1 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в gz1 |
p1 рт gh в g(z2 h) p2 . |
|
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из первых двух уравнений имеем: |
|
|
|
|||||||||||||
|
v |
V |
|
|
4V |
, v |
|
|
|
V |
|
|
|
4V |
. |
|
|
(а) |
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
S1 |
|
|
d12 |
|
|
S2 |
|
|
d22 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Из |
четвѐртого |
уравнения |
|
|
подставим |
||||||||||||||||||||
в gz1 |
p1 в третье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
в |
(v2 |
v2 ) gh( |
|
|
). |
|
|
|
|
|
|
||||||||||||
|
|
|
рт |
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим значения v1 |
и v2 |
из (а): |
|
|
|
Рис. 2.6 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8V |
2 1 |
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gh(рт в ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
4 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
|
d1 |
|
|
||||
Отсюда
27
V |
|
(рт в )g h |
|
0.12 |
м3 |
. |
|||||
|
|
1 |
|
1 |
|
|
с |
||||
|
|
|
|
|
|
|
|||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
||||
|
|
|
в |
|
|
|
|
|
|
||
|
|
|
d2 |
|
d1 |
|
|
|
|
|
|
2.7. Скорость ударной волны
Гидравлический удар – резкое увеличение давления в трубопроводе при внезапной остановке движения в жидкости.
Гидравлический удар возникает при быстром закрытии задвижки, крана, при внезапной остановке насоса. Особенно опасен гидроудар в длинном трубопроводе, в котором движется большая масса жидкости с большой скоростью.
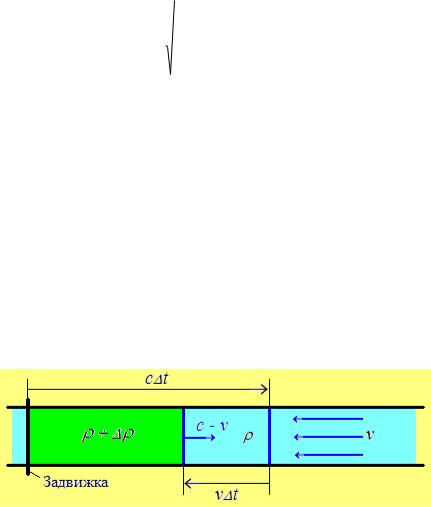
Представим себе горизонтальную трубу постоянного сечения S , в которой жидкость или газ, имеющий плотность и давление p, движется влево со средней скоростью v (рис. 2.7).
Рис. 2.7
В момент времени t 0 быстро закроем задвижку. Передний, первый слой жидкости, столкнувшись с задвижкой, отразится вправо. Однако на него набежит второй слой, увеличит в нѐм давление и отразится. На второй слой набежит третий, увеличит давление и отразится. И т.д.
Таким образом, граница участка повышенного давления p p и повышенной плотности будет перемещаться в правую сторо-
ну, против течения жидкости, с некоторой скоростью, называемой
скоростью распространения волны давления (или ударной волны).
Обозначим через c скорость распространения волны давления в неподвижной жидкости. За время t волна давления должна была бы пройти вправо путь c t (рис. 2.6). Однако за это время набегающее течение снесѐт волну давления назад на расстояние v t. Поэтому в действительности волна давления пройдѐт путь
c t v t (c v) t.
28
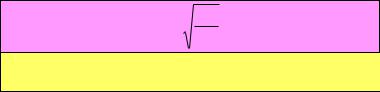
Объѐм этого участка V S (c v) t, масса m ( )S(c v) t. До момента t 0 (до столкновения с задвижкой) эта масса имела
скорость v, а значит импульс m v ( )S(c v) t v. |
|
Через время t эта масса стала неподвижной (v 0), |
поэтому еѐ |
импульс стал равен нулю. Следовательно, за время t |
произошло |
изменение импульса, равное ( )S (c v) t v. |
(а) |
С другой стороны, за время t давление на задвижку возросло наp, поэтому сила на задвижку возросла на S . Значит, за время
t произошло изменение импульса силы, равное S p t. |
(б) |
Так как величины (а) и (б) равны, то |
|
S p t ( )S (c v) t v, или p ( )(c v) v. |
(в) |
На участке трубы длиной (c v) t располагается сжатая |
масса |
m ( )S (c v) t. Если бы масса m не была сжата, она имела бы первоначальную плотность и занимала бы участок длины c t, т.е. было бы m Sc t. Значит, ( )S (c v) t Sc t,
или c ( )(c v). |
(г) |
Равенства (в), (г) образуют систему уравнений |
|
p ( )(c v) v, |
|
|
|
c ( )(c v), |
|
из которой находим p cv, |
(д) |
Раскрыв скобки во втором уравнении системы, |
будем иметь |
v (c v). |
|
Обычно v c, т.е. скорость движения частиц пренебрежимо мала
по сравнению со скоростью распространения ударной волны. Поэтому v c. Подстановка в (д) даѐт
с |
p |
|
. |
(2.11) |
Формула вычисления скорости ударной волны,
а также скорости звука в жидкости или газе
2.8. Скорость звука в газе
Зависимость плотности от давления ярко проявляется у газов: при увеличении давления на газ его плотность увеличивается. Кроме того, газ при сжатии нагревается. Теплопроводность у газа мала, поэтому тепло не успевает уходить из нагретых областей. Это значит, что для газа сжатие является адиабатным процессом (т.е. без
29
передачи тепла). Адиабатный процесс для идеального газа описывается уравнением
pV const, |
(а) |
в котором константа |
называется показателем адиабаты, 1. |
При сжатии масса не меняется. Пусть m, V – масса газа и его
объѐм. Тогда V |
m |
|
m |
||
|
. Подставив в (а), получим |
p |
|
|
|
|
|
||||
|
|
|
|
|
|
p C2 ,
где C2 mC1 . Получили связь между p и .
Из (2.12) находим
Из (2.12) следует
Подставим в (2.13):
Отсюда p p .
dp C2 1d.
C2 p .
dp p d.
Подставив в (2.11), будем иметь
cг 
 p .
p .
C1 , или
(2.12)
(2.13)
(2.14)
(2.15)
Получилась формула определения скорости звука в газе.
2.9.Решение уравнения Эйлера для газа
исжимаемой жидкости
Воспользуемся равенством (2.9), в котором не использовалось условие несжимаемости. Подставим (2.13) в (2.9). Получим
|
v2 |
|
|
1 |
|
|
|
|
|
|
|
|
gz C |
|
|
C |
. |
|
|
(а) |
|
|
|
|
|
|
||||||
2 |
2 |
|
1 |
3 |
|
|
|
|
||
|
|
Пусть при z z0 |
выполняются условия: p p0 , |
0 , |
v v0. |
(б) |
||||
Подставим их в (а): |
|
|
|
|
|
|||||
30
