8 Механический расчет

Вал любого роторного агрегата является его важнейшей составной частью, поскольку производительность, точность технологических операций, ресурс агрегата и другие важные показатели зависят прежде всего от динамических перемещений и напряжений в материале вала. К валу непосредственно примыкают многие узлы и детали ротора и статора, надежность и экономичность которых в первую очередь зависят от работоспособности и размеров вала.

Расчету вала предшествует разработка его расчетной схемы, отражающей лишь наиболее важные факторы исключающей все те несущественные особенности, которые не могут сказаться ни на точности расчета, ни на работоспособности агрегата в целом. Так, материал вала считается сплошной однородной, изотопной средой с идеальной упругостью, а деформации вала - малыми по сравнению с его размерами.

Главными критериями работоспособности валов являются виброустойчивость, жесткость и прочность.

8.1 Расчет валов на виброустойчивость

Расчет вала на виброустойчивость по точному методу А. Н. Крылова усложняется, если число сосредоточенных масс (дисков) оказывается больше единицы. В связи с этим в практике химического машиностроения получил распространение так называемый метод приведения, основанный на исследованиях академика Ю. А. Шиманского.

Метод приведения, достаточно точный для инженерных расчетов, позволяет наглядно представить влияние многочисленных факторов на критическую скорость и тем самым способствует рациональному конструированию роторов. Метод базируется на использовании следующих известных формул, которые для удобства вычислений даны в безразмерном виде.

Рисунок 13 - Корни частотного уравнения для вала: а - консольного, б - однопролетного

Относительный приведенный коэффициент жесткости вала:

консольного (рисунок 14, а, б)

; (35)

однопролетного (рисунок 15, в, г)

, (36)

где - приведенный коэффициент жесткости вала, Н/м;

- момент инерции сечения вала на опоре Б, м⁴;

- относительная текущая координата, - для консольного вала,- для однопролетного вала;

- относительный диаметр вала в точке с координатой z, ;

- относительный прогиб вала в точке с координатой z, ; (здесь- прогиб вала в точке приведенияВ, м).

Относительная приведенная масса вала:

консольного

; (37)

однопролетного

, (38)

где - приведенная масса вала, кг;

- диаметр вала на опоре Б, м.

а, в - реальные валы со многими сосредоточенными массами ;б, г - идеализированные расчетные схемы валов с одной приведенной массой , сосредоточенной в точке приведенияВ

Рисунок 14 - К расчету консольного (а, б) и однопролетного (в, г) валов по методу приведения

Относительная приведенная масса i-го конструктивного элемента установленного на валу:

консольном

, (39)

где т_{1i пр} - приведенная масса элемента (диска, мешалки, барабана и т. п.) массой m_1i , установленного на консоли вала, кг;

однопролетном

, (40)

где т_{i пр} - приведенная масса элемента, имеющего массу m_i , кг.

Относительная приведенная масса вала и элемента, установленных на валу:

консольном

; (41)

однопролетном

. (42)

Относительная критическая скорость вала

. (43)

Переход от безразмерного значения критической скорости к ее размерному значению осуществляется для консольных и однопролетных валов сплошного поперечного сечения соответственно по формулам, вытекающим из выражений (35)—(43):

; . (44)

Таким образом, реальный вал сложной конструкции, нагруженный несколькими массами, в том числе и собственной массой, в рассматриваемом методе заменяется более простой идеализированной моделью вала (рисунок 14, б, г) с одной сосредоточенной приведенной массой (консольный) или(однопролетный) и приведенными параметрами, вычисляемыми по формулам (35)—(43). За точкуВ приведения распределенных и сосредоточенных масс принято место крепления массы на консоли (рисунок 14, а) и середина пролета для однопролетного вала (см. рисунок 14, г), а форма осиизогнутого вала считается совпадающей с формой оси при статическом изгибе вала поперечной силой, приложенной в точке приведения, и определяется следующими уравнениями:

консоль БВ консольного ступенчатого вала

; (45)

; (46)

где - эквивалентный момент инерции сечения вала в пролетеАВ, определяемый по формулам (53) и (54);

однопролетный вал постоянного поперечного сечения и пролет АБ консольного вала

. (47)

Как показывают расчеты, однопролетные валы нецелесообразно выполнять с переменным сечением по длине (конструктивные ступени вала, имеющие диаметр, отличающийся на ±10 % от диаметра рала d_в в точке приведения В, в расчетах допустимо не учитывать).

Однако консольные валы целесообразно проектировать ступенчатыми, близкими по форме балке равного сопротивления изгибу (см. рисунок 15), что позволяет уменьшить массу ротора и несколько увеличить его .

Диаметр вала d_Б в опорном сечении Б рассчитывается по формуле

, (48)

где для виброустойчивого вала: консольного при :

; ; ;

Рисунок 15 - Расчетная схема консольного ступенчатого вала с сосредоточенными массами т_1i на консоли вала

консольного при ;

; ;;

однопролетного при ;

; ;.

Приведенная масса элементов определяется по формулам:

для консольного вала

, (49)

для однопролетного вала

(50)

Формула (48), позволяющая быстро выполнить проектный расчет виброустойчивого вала, получена на основе условий (35)-(44).

После определения диаметра d_Б по формуле (48) необходимо вычислить диаметры d_A и d_B из условий прочности при кручении, а диаметры ступеней d_Al, d_A2, d_A3 в пролете вала принять из конструктивных соображений d_Ai d_A с учетом закрепления на валу тех или иных деталей. Диаметры ступеней на консоли необходимо принять в соответствии с формулой

. (51)

Условие (51) позволяет замкнуть систему уравнений (35)—(43) и получить расчетную формулу (44) для ступенчатого многомассового вала. При этом показатель степениt формулы (51) выбирается согласно рисунку 16 в зависимости от относительной приведенной массы элементов и относительной податливости пролета

. (52)

Эквивалентный момент инерции пролета с двумя ступенями d_Al, d_A2 (см. рисунок 15) рассчитывается по формуле

(53)

и с тремя ступенями d_A1, d_A2, d_A3 - по формуле

, (54)

где ;.

Тогда ,

где

;(55)

(56)

(57)

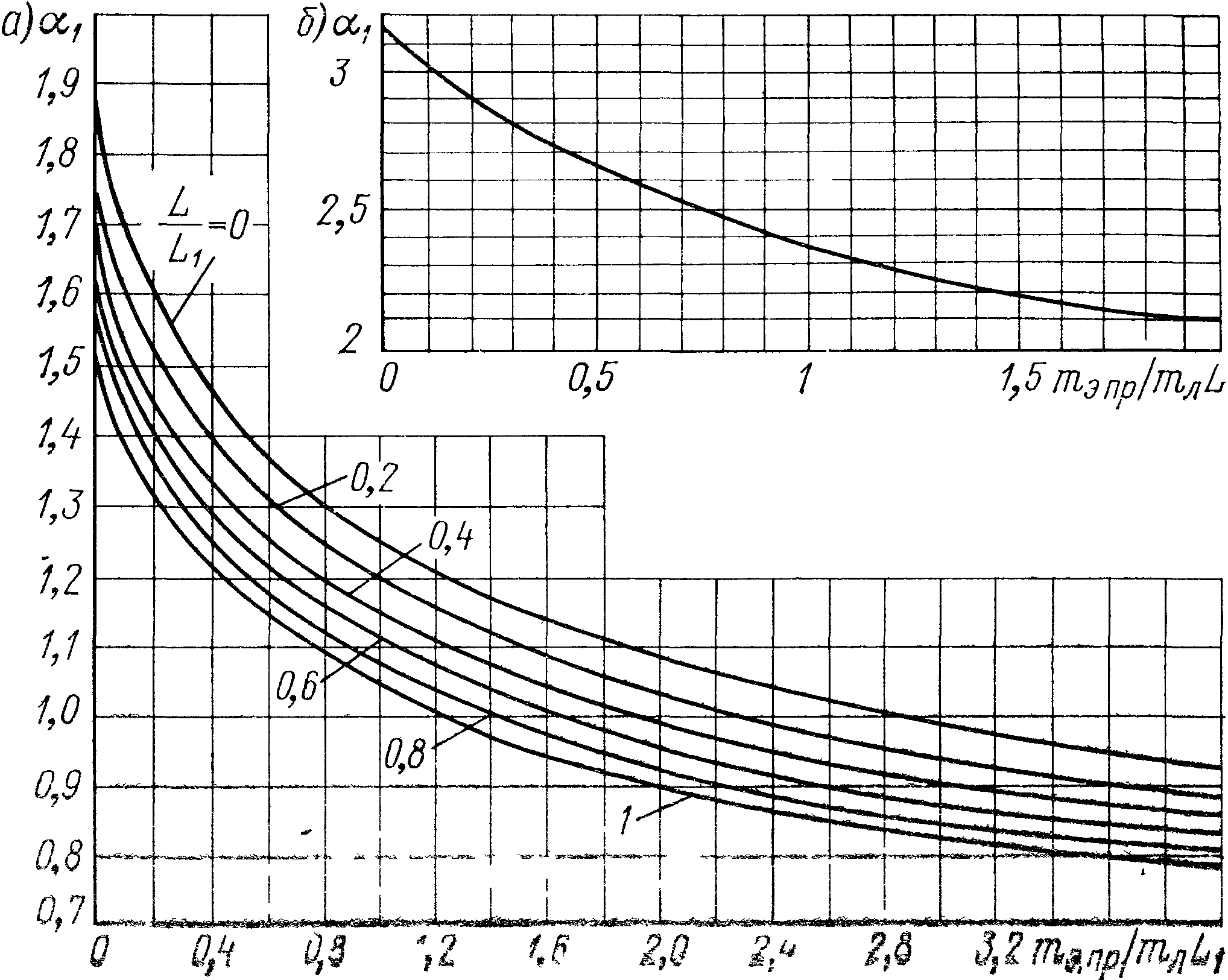
Рисунок 16 - Зависимость показателя степени t от параметров относительной приведенной массы установленных элементов и относительной податливости пролетаконсольного ступенчатого вала

Изложенная выше методика касалась проектного расчета вала. При проверочном же расчете, когда значение d_Б задано, необходимо определить по формуле (44). Приd_B = d_Б = const, т. е. b₁ = 0 (консоль постоянного по длине поперечного сечения), что часто встречается на практике, формула для упрощается:

. (58)

Зависимость (58) приведена на рисунке 17 в виде графика, способствующего ускорению расчетов валов на виброустойчивосгь.

Для консольных валов постоянного поперечного сечения расчет еще более упрощается, так как d_Б = d_B = d_A = d; ;, и формулы (46) принимают вид

; .

Это позволило уравнения (45) и (47) представить на рисунке 18 в виде графиков, способствующих также ускорению расчета валов.

Для однопролетного вала постоянного поперечного сечения и. Вычислив по формулам (41), (42), (49), (50), легко получить далее по формуле (43)и найти по формуле (44) размерное значение критической скорости однопролетного вали заданного поперечного сечения.