Моя РПР

Расчетно-проектировочная работа №1

Тема: Расчет на прочность балки при изгибе

Исходные данные

q = 18 кН/м;

[] = 160 МПа (сталь);

Е = 2∙10⁵ МПа;

[]_р = 20 МПа (чугун);

[]_сж = 80 МПа (чугун);

a = 1 м.

Исходная схема нагружения изображена на рисунке 1.

Рисунок 1 – Исходная схема нагружения

Решение

1. Вычерчиваем расчетную схему балки (рисунок 2). Определяем реакции опор и строим эпюры поперечной силы и изгибающего момента.

Направив реакции опор в точке B вверх и в точке С вверх (горизонтальная реакция Н_С заведомо равна нулю), составим уравнения моментов относительно опор B и С

(1)

Отсюда находим R_В

Аналогично уравнение моментов относительно опоры В

(2)

Отсюда находим V_С

Для проверки составим уравнение равновесия относительно оси y

y = 0: V_c + R_в – q ∙ 3а - F = 0. (3)

2,3qa + 1,7qa – 3qa – qa;

4qa + 4qa = 0:

Условие проверки выполняется, значит проведенные выше вычисления верны.

Разбиваем балку на три силовых участка CD, АC, ВС; для каждого участка применяем метод сечений и составляем уравнения поперечной силы и изгибающего момента.

Определяем характерные ординаты поперечной силы и изгибающего мо-

мента и строим их эпюры (рисунок 2).

Рассмотрим участок CD:

; (4)

;

; (5)

Аналогично рассмотрим участок AС:

; (6)

(7)

Аналогично рассмотрим участок AB:

0 ≤ z₃ < 2a;

(8)

(9)

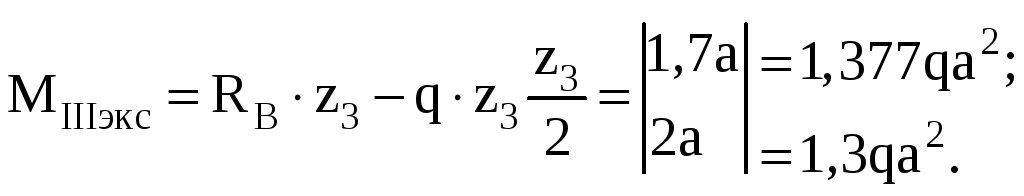(10)

Эпюра изгибающих моментов построена на растянутом волокне (рисунок 2)

Рисунок 2 – Расчетная схема балки

2  Производим подбор сечений балок из условия прочности по нормальным напряжениям

(11) где М_{и мах} = ;

М_{и мах} = = 24,8 кН∙м.

Отсюда находим расчетный осевой момент сопротивления сечения:

(12)

Выполняем подбор сечений стальной балки в следующих вариантах.

а) Стальное двутавровое по ГОСТ 8239-89 (рисунок 3).

По сортаменту выбираем двутавр №18a, для которого W_x = 159 см³.

Площадь сечения двутавра A_дв = 25,4 см².

Так как расчетный момент сопротивления меньше, чем момент сопротивления для двутавра по сортаменту, следовательно, считаем процент недогрузки двутавра

б) стальное прямоугольное, (рисунок 4).

Р исунок 3 – Двутавровое сечение

Осевой момент сопротивления находим по формуле

(13)

Откуда ширина b равна

(14)

Принимаем b кратное двум, т.е. b = 62 мм, тогда h = 124 мм.

Площадь прямоугольного сечения

(15)

Р исунок 4 – Прямоугольное сечение

в) стальное круглое (рисунок 5).

Осевой момент сопротивления

(16)

Откуда диаметр d

(17)

Принимаем d = 118 мм.

Площадь круглого сечения определяется по формуле

(18)

Рисунок 5 – Круглое сечение

Выполняем сравнение экономичности сечений стальной балки по их площадям

Таким образом, можно сделать вывод о том, что самым целесообразным

является двутавровое сечение.

г) чугунное тавровое сечение (рисунок 6)

Предварительно найдем геометрические характеристики сечения.

Определяем координаты центра тяжести.

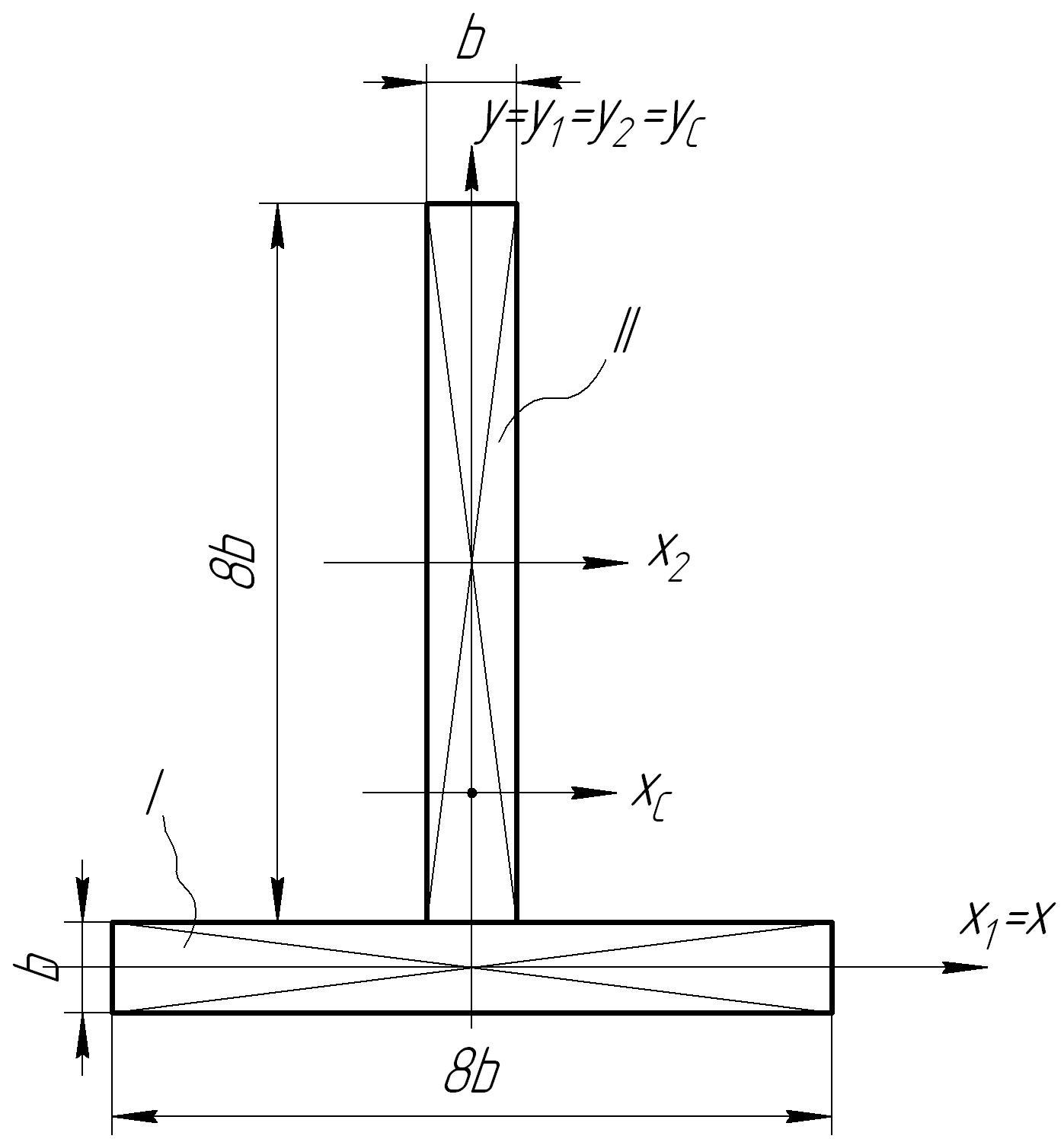
Рисунок 6 – Чугунное сечение

Выбираем оси (x, y) начальной системы координат, относительно которых определяем координаты (x_i, y_i) составных частей сечения:

x_i = 0;

y_i = 0;

х₂ = 0;

.

Находим площади составных частей сечения

(19)

А = A₁ + A₂; (20)

А = 8b² + 8b² = 16b² .

Определяем координаты центров тяжести. Так как сечение симметричное, то ось у и совпадают:

;

; (21)

,

где - ординаты центра тяжести элементов сечения относительно оси x.

.

Определяем центральный осевой момент инерции сечения на основании теоремы сложения. Через найденный центр тяжести сечения проводим новые вспомогательные оси х_с и у_с, параллельные осям х и у, и вычисляем осевой момент инерции сечения относительно этих осей, пользуясь формулами перехода к параллельным осям:

(22)

(23)

(24)

где - осевые моменты инерции сечения,

- ординаты центра тяжести элементов сечения относительно оси .

равны:

равны:

Подставляя найденные числовые значения в формулы (23) и (24), получим

Подставляем найденные значения в формулу (22)

Располагаем заданное сечение рационально, учитывая, что чугун хуже сопротивляется растяжению, чем сжатию. Для этого, глядя на эпюру изгибающих моментов, сечение переворачиваем так, чтобы в растянутой зоне напряжения были меньше по модулю, чем в сжатой зоне (рисунок 7).

σсж

усж

н.л.

ур

σр

Рисунок 7 – Расположение сечения оптимальным образом

Определяем осевые моменты сопротивлений для растянутых и сжатых слоев сечения балки

(25)

(26)

Подставляем числовые значения, получим

Определим размеры сечения чугунной балки по сжимающим и растягивающим волокнам

(27)

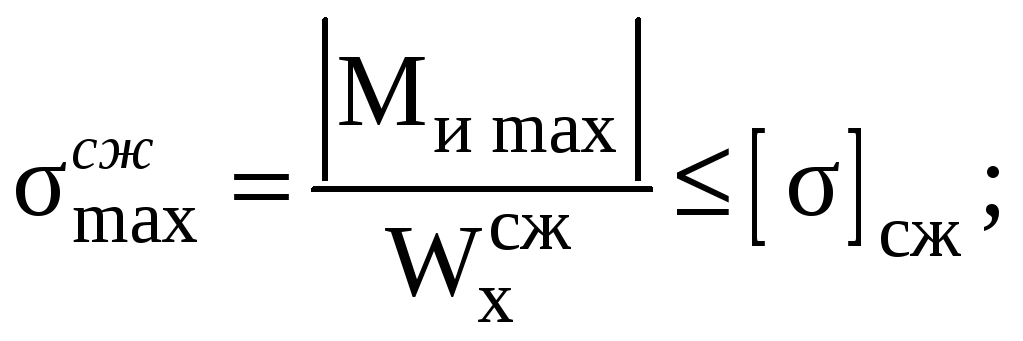(28)

Откуда получим:

Подставляем числовые значения, получим

Найдем площадь сечения

Анализируя выше рассмотренные сечения, видим, что наиболее экономичным является двутавровое сечение, т.к. в этом случае будет меньший расход материала; это показывает следующее соотношение площадей

3 Построим все сечения в одном масштабе с эпюрами нормальных напряжений (рисунок 8). Для чего найдем нормальные напряжения для всех сечений по формуле:

(29)

Результаты вычислений приведены в таблице 1.

Таблица 1 – Результаты расчета нормальных напряжений

	Двутавр	Прямоугольник	Круг	Тавровое сечение
	159	158,9	161,2
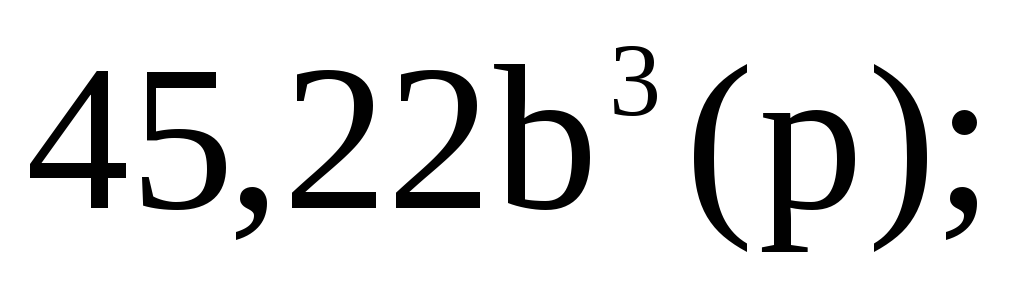
	155,9	156	153,76	20,3
	155,9	156	153,76	46,15

Рисунок 8 – Сечения стальной, чугунной балки с эпюрами нормальных

напряжений

4 Проводим полную проверку прочности для балки двутаврового профиля.

4.1 Выполняем проверку прочности по опасным точкам второго типа (т.С), используя следующие данные и формулы: h=180мм; b = 100 мм; b₀ = d = 5,1 мм; t = 8,3 мм; I_x = 1430 см⁴; S_x = 89,8 см³; Q_max = 1,3qa.

(30)

Допускаемое касательное напряжение найдем по III теории прочности:

τ = 0,5 ∙ [σ]; (31)

τ = 0,5 ∙ 160 = 80 МПа.

Подставляем числовые значения, получим

Отсюда следует, что условие прочности выполняется

4.2 Определяем нормальные , касательные и главные напряжения в опасных точках сечения балки (т.А), где одновременно возникает неблагоприятное сочетание большого изгибающего момента и поперечной силы по формулам:

(32)

(33)

(34)

где

- площадь отсеченной части сечения, см²;

S_x^отс – статический момент отсеченной части сечения, см³; b_i – ширина сечения, см;

I_x – момент инерции сечения, см⁴.

Полученные данные сводим в таблицу 2.

Таблица 2 – Результаты расчета напряжений двутавровой балки

	уi, см	, МПа	см2	см	см3	см	МПа	МПа	МПа
1	-9	-147,3	0	-	0	-	0	0	-147,3
2	-8,17	-133,7	8,3	8,58	71,2	10	0,27	0,0005	-133,7
2|						0,51	5,27	0,2074	-133,9
3	0	0	-	-	89,8	0,51	6,65	6,65	-6,65
4|	8,17	133,7	8,3	8,58	71,2	0,51	5,27	133,9	-0,2074
4						10	0,27	133,7	-0,0005
5	9	147,3	0	-	0	-	0	147,3	0

Статический момент отсеченной части сечения определяется по формуле

. (35)

По полученным значениям напряжений строим эпюры нормальных , касательных и главных напряжений (рисунок 9).

Рисунок 9 – Эпюры нормальных, касательных и главных напряжений для двутавровой балки

4.3 Для опасной точки третьего типа определяем графически главные напряжения, для чего строим круг Мора (рисунок 10). Опасными точками 3-го типа являются точки 4^| и 2^|, выбираем точку 4^|, для которой = -0,2074 МПа.

4.4 Проверяем прочность в точке 4^| по четвертой теории прочности согласно неравенству:

Таким образом, сечение прочно по главным напряжениям.

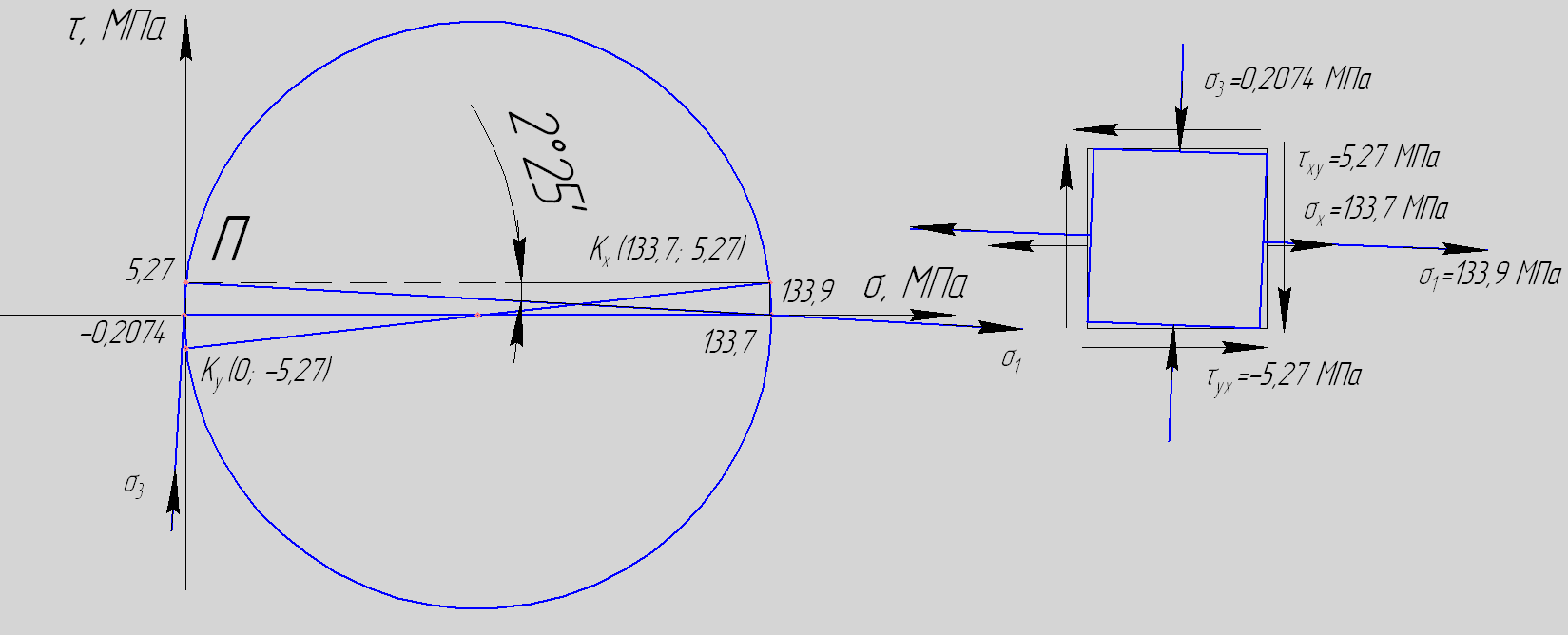
Рисунок 10 – Расчетная схема напряженного состояния

5 Пользуясь универсальным уравнением метода начальных параметров, определим линейные и угловые перемещения.

Составляем универсальное уравнение упругой линии балки (УУУЛБ), используя универсальное уравнение

(37)

где y(z) - прогиб на последнем участке заданной балки, мм;

y₀ - геометрический начальный параметр, прогиб, мм;

- угол поворота в начале координат, град;

- статический начальный параметр, момент,

Q₀ – поперечная сила в начале координат,

- действующий внешний момент,

F_i – внешняя сила, Н;

q_i – внешняя равномерно распределенная нагрузка, Н/м;

- абсциссы точек приложения внешних нагрузок, м.

Выбираем начало координат в крайнем левом сечении балки и считаем его общим для всех участков. До этого переворачиваем балку точкой опоры В влево в начало координат (рисунок 11).

Рисунок 11 – Схема нагружения для определения прогиба и угла поворота

Для последнего правого участка заданной балки составляем УУУЛБ

(38)

Находим начальные параметры у₀ и из граничных условий