2.3. Расход жидкости

Расход – это объём жидкости, протекаю­щей сквозь воображаемую проницаемую поверхность за единицу времени.

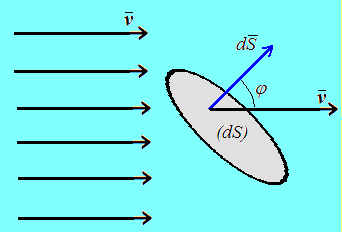
В пространство, где течёт жидкость или газ со скоро­стью поместим воображае­мую непод­виж­ную бесконечно малую площадкупро­ни­цаемую для жид­кости. На рис. 2.5 показан слу­чай, ко­гда вектор пло­щадки рас­полагается под произ­воль­ным углом к век­тору скоро­сти

Расход жидкости через площадку будет равен

(2.1)

Теперь в пространство, где течёт жидкость или газ, по­местим произвольную по­верхность Мысленно ра­зобьёмна бесконечно ма­лые части. Расход сквозь ка­ждую часть определяется по формуле (2.1). Сложив (про­интегрировав) эти расходы, получим расход через всюРис. 2.5

Расход жидкости (газа) через поверхность

(2.2)

Если сечение перпендикулярно скорости течения:(при этоми скорость во всех точкаходина­кова, то из (2.2) будем иметь

(2.3)

Обыкновенно этой формулой пользуются при вычислении расхода жидкости или газа через поперечное сечение трубопровода.

Умножим объём (2.1) на плотность Получиммассу жидкости, протека­ющей сквозь за еди­ницу времени

(2.4)

Проинтегрировав (2.4) по поверхности получим массу жидкости, протека­ющей сквозьза еди­ницу времени (массовый расход):

Если поверхность замкнута, то по теореме о дивергенции (П.4.2) это равенство равносильно такому:

(2.5)

– масса жидкости, вытека­ющейиз области за еди­ницу времени.

Пусть область мала; обозначим её Тогда из (2.5) получим

(2.6)

– масса жидкости, вытекающейиз области за единицу времени.

З а д а ч а 1. Дано поле скоростей текущей жидкости

а) Найти расход через боковую поверхность конуса ограниченного заданными поверхностями:

(а)

б) Найти расход через всю поверхность конуса.

 Начертим конус (рис. 2.6). Равенство есть уравнение горизонтальной плоскости. Равенство есть уравнение конической поверхности.

а) Уравнение конической поверхности запишем так:

Находим нормальный вектор

_{Рис. 2.6}

После сокращения на +2 будем иметь

При этом вектор укорачивается, но направление не меняется. Его модуль

Единичный вектор, нормальный к боковой поверхности конуса, равен

Находим скалярное произведение:

Подставим в формулу расхода (2.2):

На поверхности конуса выполняется равенство Подставим это значение:

где круг,проекция боковой поверхности конуса на плоскость Из системы уравнений (а) получим или окружность радиуса

Для вычисления интеграла перейдём к полярной системе координат Тогда и

Ввиду того, что

остаётся

Отрицательность расхода означает, что жидкость в основном втекает через боковую поверхность конуса.

б) Вся поверхность конуса является замкнутой поверхностью, внутри которой находится весь конус поэтому можно воспользоваться формулой Остроградского-Гаусса. Но сначала найдём дивергенцию вектора скорости:

По формуле расхода (2.2) имеем



2.4. Расход при стационарном течении.

Течение называют стационарным, когда скорость не зависит от времени.

Рассмотрим течение жидкости в каком-либо трубопроводе через поперечные сечения иЗа единицу времени через сечениевтекает объёма черезвытекает объёмТак как жидкость практически несжимаема, то в пространстве междуиобъём жидкости не меняется. Значит, объём входящей жидкости через сечениеравен объёму выходящей жидкости черезИначе говоря,. Таким образом,

Условие постоянства расхода

(2.7)

Следовательно, там, где сечение больше, скорость меньше.