Глава 2 динамика невязкой жидкости

Гидродинамика – раздел МСС, в котором рассматриваются условия и закономерности движения жидкостей и газов под действием приложенных сил.

2.1. Скалярное и векторное поля

Время будем обозначать произвольную точку в пространстве –

Поле – функция от точки и времени.

Так как функция может быть скалярной либо векторной, то и поле бывает скалярным или векторным.

Обычно рассматривают физические поля, т.е. функции, являющиеся физическими величинами. Примеры физических полей:

– плотность это скалярное поле (поле плотностей, поле плотности);

– скорость это векторное поле (поле скоростей, поле скорости).

Поле, не меняющееся во времени, называют стационарным или установившимся.

В этом случае вместо пишем а вместо пишем

В пространстве введём систему координат Произвольная точкабудет иметь координатыпоэтому вместоиможно писатьи

Подробно о полях сказано в Приложении, п. 1.

П р и м е ч а н и е. Каждый вектор в пространствеможно спроецировать на оси координат и получить три координаты. Если их обозначитьто векторможно написать либо в полной форме в виде суммы:

либо в краткой:

2.2. Линии тока и траектории

Линия тока – воображаемая линия, идущая вдоль векторов поля скоростей (рис. 2.1).

Рис. 2.1 Рис. 2.2

Итак, векторы касаются линий тока. Как найти уравнение какой-нибудь линии тока?

В пространстве введём систему координат Тогда скорость будет задаваться тремя координатами т. е. На линии тока выделим бесконечно малый кусочек и получим вектор (рис. 2.2). Так как векторы и лежат на одной прямой, их координаты пропорциональны:

Уравнения линии тока

Переменные величины являются координатами переменной точкиМ, бегущей по этой линии.

В нестационарном поле векторы могут менять свои направления. Вместе с ними и линии тока с течением времени могут менять свою форму. Значит, линии тока – это воображаемые линии, соответствующие фиксированному моменту времени, их мгновенная фотография. По линиям тока двигались бы частицы, если бы их скорости оставались такими же, как в этот фиксированный момент времени.

Если поле скоростей стационарно, то линии тока не меняются и совпадают страекториями движущихся частиц.

Траектория– это линия, по которой движется частица.

Траектория определяется системой уравнений

З а д а ч а 1. Дано поле скоростей жидкости Найти линии тока и траектории движущихся частиц.

 Имеем: – координаты скорости.

1) Линии тока задаются двумя дифференциальными уравнениями:

Решаем первое уравнение: Так как время фиксировано, то интегрированием получим

Решаем второе уравнение: Подставим найденное значение Отделим переменные, и проинтегрируем обе части. Получим

Итак, линии тока описываются системой уравнений

(а)

Найдём линию тока, которая в мо­мент проходит через точку Подставив данные значе­ния в (а), получим Значит,

Рис. 2.3 Рис. 2.4

Наличие переменной говорит о том, что с течением времени эта ли­ния изменяет свою форму и положе­ние в пространстве. Так, в мо­мент времени линия тока зада­ётся системой

а в момент эта линия превратится в линию

Графики этих линий показаны на рис. 2.3 и 2.4.

2) Траектории частиц задаются тремя дифференциальными уравнениями:

где точки над буквами обозначают производные по времени. Например,

Первое уравнение (оно линейное) имеет решение Решение третьего уравнения Подставим эти значения во второе уравнение. Получим Его интегрирование даст Значит,

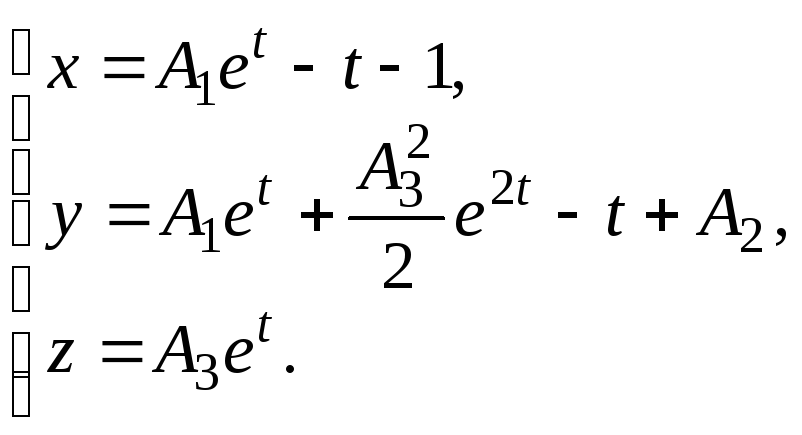(б)

Мы нашли уравнения траекторий.

Покажем, что эти траектории не совпадают с линиями тока (а). Из третьего уравнения системы (б) имеем Подставим в остальные равенства:

Обозначив получим

Видим, что эта система уравнений отличается от (а). 