1.4. Закон Архимеда

_{Выталкивающая сила направлена вверх и равна весу жидкости (газа) в объёме погруженной части тела.}

Посмотрите на рис. 1.9. Нижняя часть тела находится в слоях с большим давлением, чем верхняя. Этим и объясняется существование выталкивающей (архимедовой) силы .

Заменим тело жидкостью. Пусть масса жидкости, замещающей тело, равна (рис. 1.10). Уровень жидкости при этом не изменя­ется, значит, на эту массу действует такая же выталкивающая сила, что и на тело.

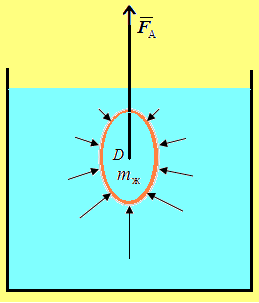
Рис. 1.9 Рис. 1.10

Масса неподвижна, следовательно, действующая на неё архимедова сила уравновешена силой тяжести

Правая часть представляет собой вес жид­кости:

Строгое доказательство формулы дано в Приложе­нии 2.

Архимедова сила прилагается к точке –центру давления жид­кости.

Пусть силы ине лежат на одной вертикали (рис. 1.11). В таком случае вращательный момент этих сил не будет равным нулю, и он заставит тело повернуться так, чтобы обе силы расположились на одной вертикали. Эти Рис. 1.11

силы отвечают за устойчивость морских и

речных судов.

Если вес тела меньше выталкиваю­щей силытело будет всплывать до тех пор, пока эти силы не сравняются. Поэтому выполнение равенства

есть условие плавания тела.

З а д а ч а 1. Резервуар, имеющий собственный вес высоту и квадратное основание со стороной заполнен бензином и погружён в воду (рис. 1.12). Определить давление р на дно резервуара и глубину погружения, если (Объёмом стенок резервуара пренебречь.)

 На дно резервуара давит столб бензина высотой поэтому

Ре­зервуар с бензином плавает, поэтому выполняется условие (а)

Объём бензинаобъём подводной части(на рис. 1.12 этот объём ограничен пунктирной линией). Поэтому

Подстановка в (а) даёт

Отсюда

 Рис. 1.12

1.5. Жидкость в неинерциальной системе отсчёта

Рассмотрим две задачи.

1. Сосуд с жидкостью плотности движется поступательно спостоянным горизонтальным ускорением (на рис. 1.13 влево). Найти уравнение свободной поверхности жидкости.

Свободной называется поверхность жидкости, граничащая с газом (например, с воздухом) или с вакуумом.

Введём систему координат связанную с сосудом (рис. 1.13). Относительно этой системы жидкость неподвижна, поэтому можно ис­пользовать уравнения гидростатики (1.2). Определим, какая линия получится при пересечении плоскости со свободной по­верхностью жидкости.

В задаче участвуют две пере­менные поэтому в систе­ме уравнений (1.2) оставим два уравнения.

На каждый элемент жидко­сти действует сила тяжести и сила инерции так как (на рис. 1.13 видим, что инаправлены противопо­ложно). Суммарная сила равна

Рис. 1.13

Находим массовую силу

т.е.

Подстановка в уравнения (1.2) даёт систему уравне­ний

Решаем первое уравнение:

(а)

Подставим во второе уравне­ние системы.

Значение подставим в (а):

(б)

В точке О, т.е. при давление равно

Подстановка в (б) даёт

Полученное значение подставим в (б):

На свободной поверхности _, тогда

– уравнение свободной поверхности.

2. Цилиндрический сосуд вместе с жидкостью плотности равно­мерно вращаются с угловой скоростьювокруг вертикальной оси цилиндра. Найти уравнение свободной поверхности жидкости.

Опыт показывает, что при вращении жидкость будет прижи­маться к стенке сосуда за счёт силы инерции (рис. 1.14).

Направим осьвдоль оси вращения вниз. Введём систему координатсвя­занную с сосудом. Мысленно рассмотрим произвольную частицу жидкости массыОт осик этой частице проведём векторперпендикулярныйЧастица движется с центростремительным ускоре­ниемнаправленным к оси враще­ния(рис. 1.14). Значит, на неё действует сила инерции

На частицу действует также сила тяжести Поэтому суммарная сила, действующая на частицу, равна Рис. 1.14

Находим массовую силу:

т.е.

Относительно системы координат жидкостьнеподвижна, по­этому можно использовать уравнения гидростатики (1.2):

(а)

Решение системы даёт следующий результат: свободной поверхностью жидкости является параболоид вращения:

 Выведем это равенство. Решим первое уравнение системы (а):

(б)

Чтобы найти подставим (б) во второе уравнение системы (а). Получим

Это уравнение имеет такой же вид, как и первое уравнение системы. Поэтому его решение подобно (б): Подставим это значение в (б):

(в)

Чтобы найти подставим (в) в третье уравнение системы. Будем иметь

Подставим значение в (в):

(г)

Чтобы найти воспользуемся начальным условием: в точке О: т.е. Подставив эти значения в (в), получим Подставим это значение в (г):

(д)

Применим это равенство к свободной поверхности жидкости. На всей свободной поверхности давление одинаково и равно Подста­вим это значение в (д):

отсюда

■