12. Расход невязкой несжимаемой жидкости как следствие уравнения неразрывности

1) Несжимаемость жидкости означает, что поэтомуотсюда(а)

Поток вектора сквозь замкнутую поверхностьограничивающую областьравен

|По формуле Остроградского-Гаусса|=

Итак,

(б)

Вся поверхность ограничи­вающая объёмжидкости, состоит из трёх частей: боковой поверхности трубыи сеченийи(рис. 3.6). Поэтому

Первый член суммы равен нулю, потому что сквозь боковую поверхность трубы нет течения. Значит,

(в)

На поверхности имеем(рис. 12.1), поэтому

Рис. 12.1

На поверхности имеемпоэтому

(в) или(г)

Итак, для несжимаемой жидкости выполняется равенство (г).

2) Невязкость жидкости означает, что стенки сосуда не оказывают сопротивления движению, и слои текущей жидкости не тормозят друг друга. Значит, во всех точках сеченияив сеченииВ этом случае

(г) 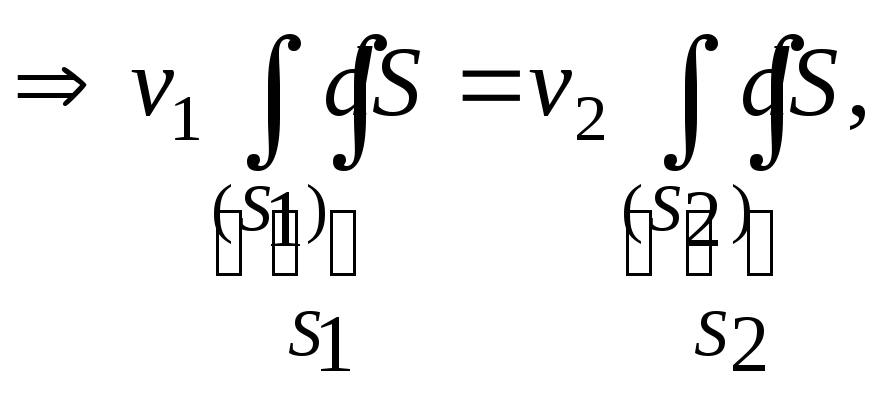илит.е.■

13. Парадокс гидростатики

В механике сплошной среды существует множество парадоксов. Рассмотрим один из них.

Два лёгких конических сосуда одинаковой ёмкости и высоты наполним водой (рис. 13.1). При их взвешивании весы покажут одинаковый результат гдемасса воды в каждом сосуде.

В сосудах высота жидкости одинакова, поэтому на дно каждого сосуда дейст­вует одинаковое давление(без учёта атмосферного давления). Поэтому на дно сосудаа действует сила на дно сосудаб действует сила Так как то

Рис. 13.1

Следовательно, весы, казалось бы, должны показывать разный резуль­тат.

Противоречие разрешается просто: весы измеряют действующую на них суммарную вертикальную силу. Так, если сложить все силы, действующие на боковую стенку сосуда а, получим суммарную силу направленную вниз (рис. 13.2). Она добавится к силетакже направленной вниз.

Рис. 13.2

А на боковые стенки сосуда б действует суммарная сила направленная вверх. Она уменьшит силунаправленную вниз. В итоге в обоих случаях суммарная вертикальная сила оказывается одинаковой, и весы покажут один и тот же вес.

14. Измерение атмосферного давления

_{Мы живём на дне воздушного океана и испытываем на себе внешнее атмосферное давле­ние, хотя его не замечаем, потому что оно уравновешено (скомпенсировано) давлением наших внутренних органов.}

Впервые атмосферное давление измерил Торичелли. Он взял стеклянную трубку длиной около 80 см, закрытую с одного конца, заполнил ртутью и опустил открытым концом в чашку с ртутью (рис. 14.1). Часть ртути выли­лась, и в трубке осталось ртути 76 см.

Этот столб ртути оказывает на горизонтальный участок давление

Рис. 14.1

_{В чашке на эту же горизонтальную плоскость действует наружное атмосферное давление, равное 1 атм. Следовательно,}

760 мм рт. ст. = 1.01· 10⁵ Па = 1 атм.

Прибор для измерения атмосферного давления назы­вается барометром. Если бы вы захо­тели уравнове­сить атмосферное давление водой, вам потребовалась бы труба длиной не менее 10.34 м. Ясно, что водяной барометр такой длины слишком велик для измерения атмосфер­ного дав­ления.

Глоссарий

_{Механика– раздел физики, излагающий о равновесии, движении тел, о взаимодействиях между ними.}

_{Сила– величина (или степень) воздействия на тело. Обозначается обычно}

_{Механика сплошной среды(МСС) – раздел физики, излагающий о равновесии, движении и свойствах деформируемых тел, жидкостей и газов.}

Сплошной – не имеющий промежутков, перерывов.

Вектор площадки – вектор, перпендикулярный площадке и длиной, равной площади площадки. Обозначается обычно или

Нормаль – то же, что перпендикуляр. Нормальный = перпендикулярный.

Перпендикуляр – прямая линия, образующая угол с другойпрямой или плоскостью.

Массовая сила – сила, приходящаяся на единицу массы вещества и независимая от присутствия других частей вещества.

Если обозначить массовую силу то или

Единица массы (единичная масса) – масса, равная единице (1 кг в СИ).

Единица времени – время, равное единице (1 секунда в СИ).

Единица площади (единичная площадь) – площадь, равная единице (1 в СИ).

Например, квадрат со сторонами единица есть единица площади.

Поверхностная (или контактная) сила – сила, действующая на поверхность в результате контакта.

Напряжение – поверхностная сила, приходящаяся на единицу площади.

Если обозначить напряжение то или

_{Давление – поверхностная сила, действующая по перпендикуляру на единицу площади.}

Газ – вещество, между движущимися молекулами которого действуют силы отталкивания.

Идеальный газ – воображаемый газ, движущиеся молекулы которого взаимодействуют между собой только при столкновениях, подобно бильярдным шарам.

_{Жидкость– вещество, молекулы которого притягиваются друг к другу, но которое ещё способно течь.}

_{Свободная поверхность жидкости– граница жидкости, соприкасающаяся с газом или с другой жидкостью.}

_{Математический аппарат – математические правила, методы, приёмы.}

Исчисление – правила символьных преобразований.