2

Методические указания посвящены решению задач анализа рычажных механизмов. Приведены краткие теоретические сведения по курсу теории механизмов и машин, рассмотрены конкретные примеры. Методические указания направлены на развитие практических навыков при выполнении курсовой работы.

Методические указания предназначены для студентов очной формы обучения факультета технологии и производственного менеджмента.

Илл. 35, список литературы – 5 наименования.

Рецензент: зав. кафедрой ТТМ и КМ ГОУВПО «МГТУ им. А.Н. Косыгина», профессор, к.т.н. В.Н. Лохманов

Подготовлено к печати на кафедре теории механизмов, приборов и машин

Подписано в печать 00.00.00 Формат бумаги 60×84/16 Бумага множ. Усл. печ.л. 3. Заказ 000 Тираж 100 ГОУВПО «МГТУ им. А.Н. Косыгина»,

119071, Москва, ул. Малая Калужская, 1 © ГОУВПО «МГТУ им. А.Н. Косыгина»,

2011

3

СОДЕРЖАНИЕ

1. Синтез и кинематический анализ кулачковых механизмов ……………...4

Введение……..………………………………………………………………….........4

1.1Краткие теоретические сведения……………………………………………….4

1.2Задание на второй лист курсовой работы…………………………………….18

1.3Порядок выполнения второго листа курсовой работы ……………………...19

1.4Синтез и кинематический анализ кулачкового механизма аналитическим методом……………………………………………………………………………...38

1.4.1 Синтез и кинетический анализ кулачкового механизма с толкателем аналитическим методом……………………………………………………………38

1.4.2 Синтез и кинематический анализ кулачкового механизма с толкателем аналитическим методом с применением программы MathCАD………………...40 1.4.3 Синтез и кинематический анализ кулачкового механизма с коромыслом аналитическим методом……………………………………………………………43

1.4.2 Синтез и кинематический анализ кулачкового механизма с коромыслом аналитическим методом с применением программы MathCАD………………...45

Список литературы…………………………………………………………………48

4

1. Синтез и кинематический анализ кулачковых

механизмов.

Введение

Кулачковые механизмы нашли широкое распространение в технике. Они успешно применяются в машинах, машинах-автоматах, станках, аппаратах, механических приборах, манипуляторах, роботах и многих других устройствах, обеспечивая разнообразные законы движения звеньев рабочих органов механизмов, в том числе – продолжительный выстой ведомого звена при движущемся ведущем звене.

Кулачковые механизмы широко применяются и в текстильных машинах. Например, в ткацких станках типа СТБ кулачковые механизмы нашли применение в батанном и боевом механизмах, в приводе ремизных рамок и компенсатора уточной нити, обеспечивая выполнение технологического процесса тканеформирования.

Внекоторых случаях закон движения ведомого звена кулачкового механизма полностью определяется характером выполняемого технологического процесса, в других случаях при заданных максимальных перемещениях рабочего звена его закон движения может назначаться разработчиком из условий обеспечения высокой степени плавности движения с отсутствием «жестких» и «мягких» ударов, обеспечения минимизации инерционных нагрузок, реакций в кинематических парах, контактных напряжений в паре ролик-кулачок, износа рабочих поверхностей кулачка и ролика и других требований.

Вкурсовой работе студенту задаются типовые законы движения и максимальное перемещение рабочего звена кулачкового механизма, допускаемые углы давления на указанных фазах подъема и опускания, угловая скорость вращения кулачка. По этим исходным данным необходимо спроектировать кулачковый механизм, найдя его основные размеры, построить центровой и конструктивный профили кулачка графическим методом, определить с помощью построения планов скоростей и ускорений для одного положения кинематические характеристики кулачкового механизма, найти радиус кривизны центрового и конструктивного профиля.

1.1 Краткие теоретические сведения

Кулачковые механизмы подразделяются на плоские и пространственные. По характеру движения ведомого звена кулачковые механизмы подразделяются на механизмы с поступательным и качательным движениями выходного звена. С целью уменьшения потерь на трение кулачковые механизмы часто снабжаются роликами. По конструктивному исполнению кулачка и ведомого звена различают механизмы с дисковыми и барабанными кулачками, с остроконечным толкателем, с плоским и роликовым толкателем и коромыслом. Замыка-

5

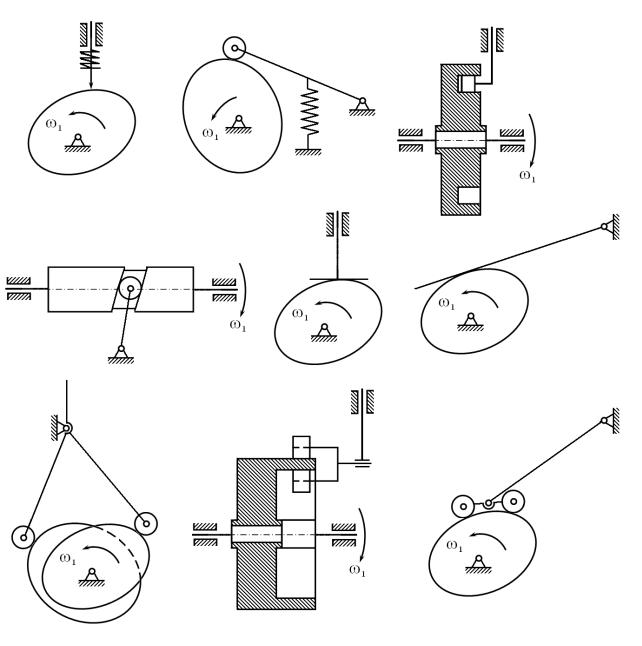
ние высшей кинематической пары обеспечивается силовым способом (пружины, грузы, пневмо-гидро-электро-магнитные устройства) и кинематическим (геометрическим) способом (кулачок и контркулачок, закрепленные на одном валу, кулачок с двумя эквидистантными профилями, т.е. кулачок с пазом или выступом). Для уменьшения сил давления и контактных напряжений ведомые звенья снабжаются несколькими роликами. Примеры перечисленных кулачковых механизмов приведены на рис. 1.

Рис. 1 Виды кулачковых механизмов

Законы движения рабочих звеньев кулачковых механизмов очень разнообразны, их количество исчисляется десятками. В качестве закона движения часто выбирается закон изменения линейного или углового ускорения ведомого звена в функции времени или вторая передаточная функция, т.е. вторая производная от перемещения ведомого звена по углу поворота кулачка.

6

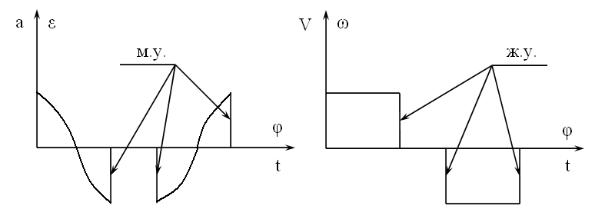
Наличие «скачка» в законе изменения ускорения или второй передаточной функции приводит к возникновению «мягких» ударов (М.У.) при работе механизма и, как следствие, появлению вибраций. Наличие «скачка» в законе изменения скорости или первой передаточной функции приводит к «жестким» ударам (Ж.У.): в механизме возникают высокие инерционные нагрузки и реакции в кинематических парах при высокоскоростных режимах. Поэтому законы последнего типа (рис. 2) рекомендуется применять при невысоких скоростях вращения кулачка.

Рис. 2 Законы движений с «мягкими» и «жесткими» ударами

В курсовой работе студенту предлагается три типовых закона движения: синусоидальный, косинусоидальный и линейный. Первый из указанных законов является плавным, безударным, два других закона вызывают появление «мягких» ударов.

Цикл работы кулачкового механизма состоит из четырех фаз: 1) фаза подъема (фаза удаления); 2) фаза верхнего выстоя (фаза дальнего стояния); 3) фаза опускания (фаза сближения); 3) фаза нижнего выстоя (фаза ближнего стояния) [1–4].

Приведем аналитические зависимости для указанных законов движения ведомых звеньев кулачковых механизмов:

1.кулачковый механизм с поступательным движением ведомого звена - толкателя

-фаза подъема (фаза удаления):

•синусоидальный закон