5.2. Оценка соответствия нормальному распределению с помощью критерия Шапиро - Уилки

Критерий Шапиро - Уилки W применяется, если число испытаний меньше 50.

Порядок расчета критерия Шапиро и Уилки:

1. Данные измерений располагаются в порядке возрастания.

2. Находят среднее значение выборки и квадрат отклонений от среднего

(36)

3. Рассчитывают коэффициент b по следующей формуле:

(37)

В таблице 7 приведены значения а для разного числа испытаний.

Таблица 7

ai	1	2	3	4	5	6	7	8	9	10
n=10	0,574	0,329	0,214	0,122	0,039
n=20	0,473	0,321	0,257	0,209	0,169	0,138	0,101	0,071	0,042	0,014

4. Находят фактическое значение критерия

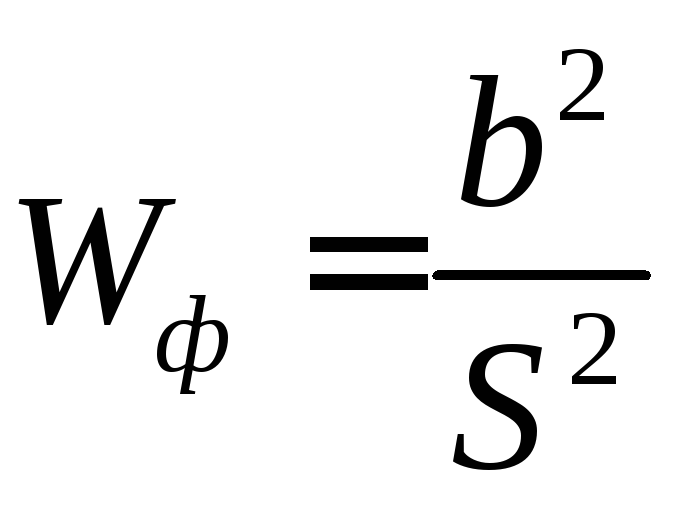(38)

5. Сопоставляют полученное значение критерия W_ф с табличным значением (таблице 8).

Таблица 8

n	3	5	10	20	30	40	50
Wт	0,767	0,762	0,842	0,905	0,927	0,940	0,947

Если W_ф>>W_т , то гипотеза о соответствии полученных результатов нормальному распределению не отвергается.

Пример.

Получены следующие результаты определения разрывной нагрузки хлопчатобумажной пряжи: 137; 151; 130; 128; 115; 134; 103; 127; 129; 144. Проверить соответствие результатов испытаний нормальному закону распределения.

1. Откроем новый рабочий лист и введем в диапазон А2:А11 этого листа результаты испытаний.

2. С помощью кнопки Сортировка по возрастанию упорядочим данные, хранящиеся в диапазоне А2:А11.

3. Выделим диапазон А7:А11, скопируем его содержимое в диапазон В2:В6. С помощью кнопки Сортировка по убыванию упорядочим данные, хранятся в этом диапазоне, в порядке их убывания.

4. Из таблицы 7 выберем значения коэффициентов а и введем их в диапазон С2:С6.

5. В диапазон D2:D6 введем формулу массива =С2:С6*(В2:В6-А2:А6) и нажмем на клавиши Ctrl+Shift+Enter. В ячейках этого диапазона появятся числа, сумма которых дает расчетное значение b = 40,00 (ячейка Е2).

6. С помощью функции СРЗНАЧ в ячейке F2 получим среднее значение выборки для диапазона А2:А11.

7. Для расчета S² сначала в диапазон G2:G11 введем формулу массива =(A2:A11-$F$2)^2 и нажмем на клавиши Ctrl+Shift+Enter. В ячейках этого диапазона появятся числа, сумма которых дает расчетное значение S² = 6164 (ячейка Н2).

8. Для расчета W в ячейку I2 вводим формулу =E2^2/H2. Получим W_расч = 0,26.

9. По таблице 8 находим табличное значение W_Т = 0,842.

Полученный результат (W_расч< W_Т) свидетельствует о том, что гипотеза с нормальном распределении результатов испытаний отвергается.

На рис. 25 приведен пример оформления расчетов в программе Excel.

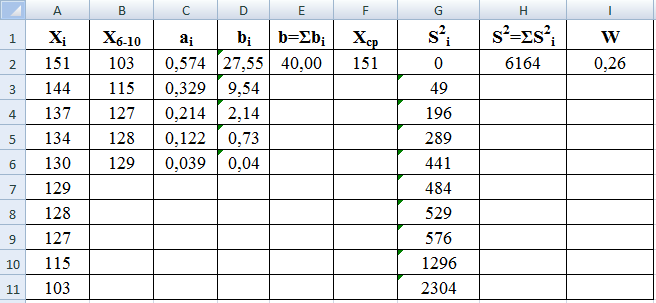
Рис. 25. Оформление расчетов в программе Excel

5.3. Оценка соответствия нормальному распределению с помощью критерия Колмогорова

При использовании λ-критерия (критерия А. Н. Колмогорова) предполагается, что теоретическая функция распределения непрерывна, а эмпирическая представлена несгруппированными данными. На практике для упрощения вычислений приходится группировать значения случайной величины на небольших интер­валах.

λ - критерий можно применять, когда для гипотетического pacпpeделения полностью известны из каких-либо теоретических соображений не только вид функции распределения, но и входящие в нее параметры. Чаще всего, однако, бывает известен вид функции, параметры определяются из опыта. При использовании критерия это обстоятельство учитывают, уменьшая число степеней свободы. Критерий λ такой поправки не предусматривает, в связи с чем eго применение в большинстве случаев приводит к завышенному согласию, если параметры теоретического распределения заранее не известны.

План расчета критерия λ:

1. Сначала находят разницу между максимальной и минимальной величинами, т.е. размах варьирования по формуле (6).

2. Определяют классовый интервал

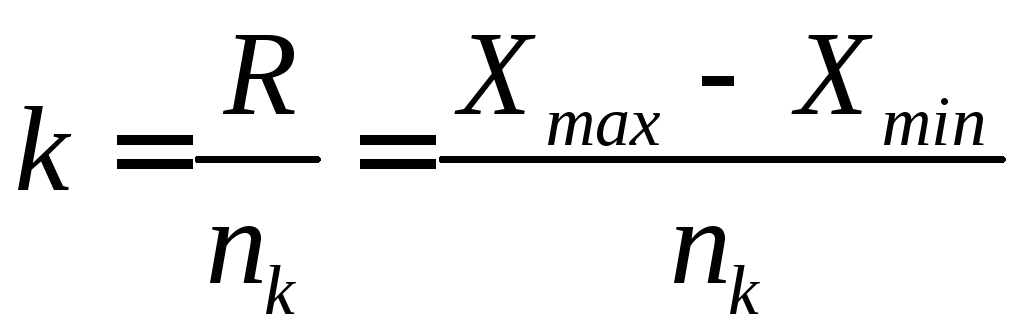
где n_k - число классов , 7<m<20.

Желательно, чтобы величина k была кратной 5 или 10.

3. Разбивают полученные значения на классы, которые располагаю по возрастанию значений, и результаты представляют в таблице.

Напротив наибольшего числа значений в классе отмечают условное отклонение , от него увеличивающиеся на единицу отклонения: вниз – положительные, вверх – отрицательные.

4.Среднее значение выборки определяют по формуле:

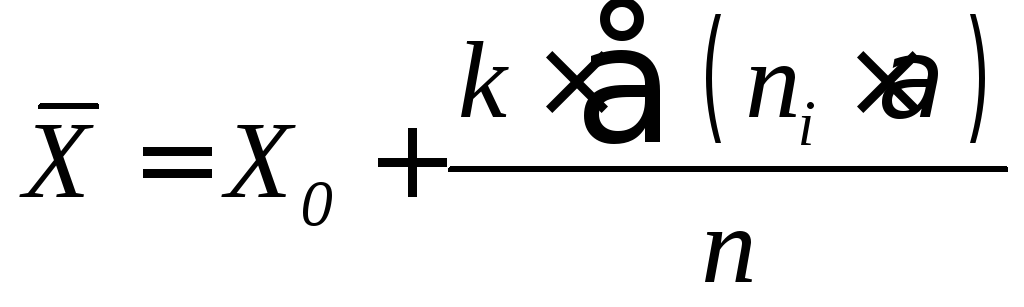
где Х – среднее значение в классе при  = 0;

k – классовый интервал;

n – общее число измерений.

5. Среднее квадратическое отклонение

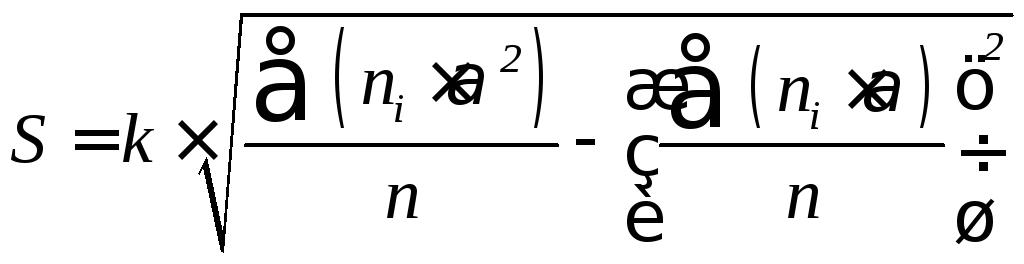
6. Составляем итоговая таблицу для расчета критерия Колмогорова (таблица 9).

7. Вычисляем эмпирические частости , а также их на­копленные значения ΣW_i. Значения ΣW_i вычисляются путем сложения величин W_i таким образом, что для каждого последующего класса оно будет равно сумме значений W_i предыдущих классов. Таким образом, для последнего класса ΣW_i=1.

8. Значения накопленных теоретических частостей ΣW определяют по величине для нормального распределения (таблица 10).

9. Далее по каждой строке расчетной таблицы вычисляют абсолютные значения разностей и обозначают максимальную из них через D_m.

Таблица 9

Границы классов

Среднее значение в классе

Число значений в классе (частота попадания в класс) yi

Условное отклонение 

yi

yi2

ΣWi

ΣW

Таблица 10

t	ΣW	t	ΣW	t	ΣW	t	ΣW
- 3,1 -3,0 -2,9 -2,8 -2,7 -2,6 -2,5 -2,4 -2,3 -2,2 -2,1 -2,0 -1,9 -1,8 -1,7 -1,6	0,001 001 002 003 003 005 006 008 011 014 018 023 029 036 045 0,055	-1,5 -1,4 -1,3 -1,2 -1,1 -1,0 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0,0	0,067 081 096 115 136 159 184 212 242 274 308 345 382 421 460 0,500	0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5	0,500 540 579 618 655 691 726 758 788 816 841 864 885 903 919 0,933	1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2.5 2,6 2,7 2,8 2,9 3,0 3,1	0,945 955 964 971 977 982 986 989 992 994 995 997 997 998 999 0,999

10. Критерий λ основан на максимальной величине расхождения D_m, между накопленными частостями эмпирического и теоретического распределения:

(39)

где n— число испытаний.

Вероятности Р (λ) того, что критерий достигнет величины λ приведены в таблице 11.

Таблица 11

λ	Р(λ)	λ	Р(λ)	λ	Р(λ)	Р(λ)	Р(λ)
0,3 0,4 0,5 0,6 0,7 0,8	0,999 0,997 0,964 0,864 0,711 0,544	0,9 1,0 1,1 1,2 1,3 1,36	0,393 0,270 0,178 0,112 0,068 0,050	1,4 1,5 1,6 1,7 1,8 1,9	0,040 0,022 0,012 0,006 0,003 0,002	2,0 2,1 2,2 2,3 2,4 2,5	0,0007 0,0003 0,0001 0,0001 0,0000 0,0000

11. Если Р(λ) <q=0,05, следовательно гипотеза о соответствии результатов испытаний нормальному закону распределения отвергается.

Если λ попадет в критическую область, т. е. если Р(λ) окажется меньше уровня значимости q, то это свидетельствует о малой вероятности такого большого значения критерия λ в условиях выдвинутой нулевой гипотезы, т. е. о неправильности гипотезы согласия, нужно искать другой теоретический закон распределения и повторить проверку гипотезы близости к нему эмпирического распределения.

В программе Excel не предусмотрен расчет критерия Колмогорова с помощью встроенных функций.