3.6.Типовые законы управления цифровыми системами.
3.6.1.Общие положения.
Требуемые характеристики цифровых систем управления в большинстве случаев обеспечиваются за счет выбора соответствующего закона управления. На практике наибольшее распространение получили типовые законы управления. Типовой закон управления в общем случае представляет композицию ( сумму ) элементарных динамических составляющих:
пропорциональной;
интегральной;
дифференциальной.
Наибольшее применение нашли следующие типовые законы управления:
пропорциональный;
интегральный;
пропорционально-интегральный;
пропорционально-дифференциальный;
пропорционально-интегрально-дифференциальный.
Техническая реализация типовых законов управления в цифровых системах управления существенно отличается от технической реализации этих законов управления в непрерывных системах. Если в непрерывных системах управления типовой закон управления реализуется аппаратно, то в цифровых системах управления типовой закон управления реализуется алгоритмически (программно).
3.6.2.Пропорциональный закон управления.
Закон
управления
Передаточная
функция регулятора
.
3.6.3.Интегральный закон управления ( метод прямоугольников ).
Закон
управления
Передаточная
функция регулятора
3.6.4. Интегральный закон управления ( метод трапеций ).
Закон
управления
Передаточная
функция регулятора
3.6.5.Пропорционально-интегральный закон управления (метод прямоугольников).
Закон
управления
Передаточная
функция регулятора
.
3.6.6.Пропорционально-интегральный закон управления (метод трапеций).
Закон
управления
Передаточная
функция регулятора
.
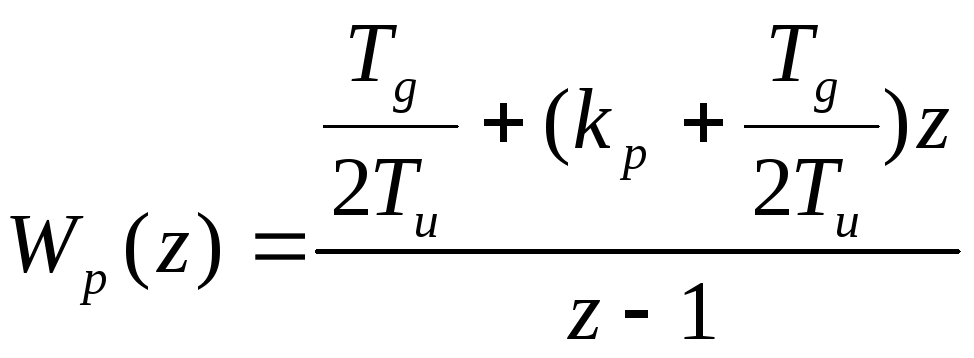3.6.7. Пропорционально-дифференциальный закон управления ( метод прямых разностей).
Закон
управления
Передаточная
функция регулятора
3.6.8. Пропорционально-дифференциальный закон управления ( метод обратных разностей).
Закон
управления
Передаточная
функция регулятора
.
3.6.9. Пропорционально-интегрально-дифференциальный закон управления (метод прямоугольников и обратных разностей).
Закон управления
Передаточная функция регулятора
.
3.6.10. Пропорционально-интегрально-дифференциальный закон управления (метод трапеций и обратных разностей).
Закон управления
Передаточная функция регулятора
.
3.6.11.Комплексные задачи.
Известно:
уравнения объекта управления;
устройство связи с объектом управления – фиксирующее звено нулевого порядка;
закон управления.
Вариант 1.
Объект управления
Закон управления – пропорциональный.
Вариант 2.
Объект управления
;
.Закон управления – пропорциональный.
Вариант 3.
Объект управления
Закон управления – пропорциональный.
Вариант 4.
Объект управления
Закон управления – интегральный.
Вариант 5.
Объект управления
Закон управления – пропорционально-интегральный.
Вариант 6.
Объект управления
Закон управления – пропорциональный.
Значения
параметров приведены в таблице
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
|
Параметр |
|
|
|
|
|
|
|
|
4 |
1 |
0,1 |
1 |
1 |
1 |
|
|
10 |
- |
- |
4 |
- |
10 |
|
|
- |
0,1 |
- |
- |
- |
1 |
|
|
1 |
0,1 |
1 |
1 |
1 |
1 |
|
|
4 |
2,5 |
15 |
- |
4 |
2 |
|
|
- |
- |
- |
10 |
0,5 |
- |
Задание:
оценить устойчивость системы управления, если система неустойчива, изменить характеристики регулятора;
оценить статическую и динамическую точность системы управления по заданию и по возмущению;
построить переходный процесс по заданию и по возмущению, оценить качество системы управления.