Отчет о лабораторной работе 3 (б) «Расчет парожидкостного равновесия в тройной смеси»

1. Алгоритм и программа расчета коэффициентов активности в многокомпонентной смеси по уравнению Вильсона.

а.) Алгоритм-блок-схема.

Коэффициенты активности в бинарной смеси рассчитываются п

Ввод исходных данных:

_ij,_ji, X_i, X_j

Расчет коэффициентов активности

по уравнениям (1) и (2) для бинарных смесей

Вывод рассчитанных коэффициентов активности

_i,_j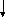

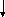
о уравнениям:

, (1)

. (2)

б.) Приведем пример программы расчета коэффициентов активности для случая бинарной пары ацетон-вода.

{Программа определения коэффициентов активности в трехкомпонентной смеси}

uses crt;

var

x, y, t : array [1..21] of real;

deltag12, deltag21, shag12, shag21 : real;

r, rr, chis1, chis2, chis3, znam, slag2, temp : real;

k, i, j, n : integer;

lymbda12, lymbda21, Pi0, nach, kon, rnew : real;

slag1, slag3 : real;

gamma : array [1..2,1..21] of real;

begin

{Массивы исходных равновесных данных}

deltag12:=41.11182; deltag21:=1880.67776;

x[1]:=1.15; y[1]:=27.91; t[1]:=92.0;

x[2]:=2.21; y[2]:=44.88; t[2]:=85.2;

x[3]:=6.38; y[3]:=68.09; t[3]:=72.1;

x[4]:=11.64; y[4]:=77.77; t[4]:=65.3;

x[5]:=17.27; y[5]:=80.73; t[5]:=62.7;

x[6]:=30.85; y[6]:=83.09; t[6]:=60.9;

x[7]:=44.39; y[7]:=84.21; t[7]:=60.3;

x[8]:=50.96; y[8]:=85.24; t[8]:=59.8;

x[9]:=52.28; y[9]:=85.12; t[9]:=59.8;

x[10]:=62.32; y[10]:=86.03; t[10]:=59.4;

x[11]:=68.29; y[11]:=87.23; t[11]:=58.8;

x[12]:=72.75; y[12]:=87.90; t[12]:=58.75;

-1-

x[13]:=76.29; y[13]:=88.71; t[13]:=58.35;

x[14]:=82.08; y[14]:=90.37; t[14]:=58.2;

x[15]:=86.55; y[15]:=92.08; t[15]:=57.7;

x[16]:=90.04; y[16]:=93.53; t[16]:=57.6;

x[17]:=92.37; y[17]:=94.72; t[17]:=57.7;

x[18]:=93.83; y[18]:=95.62; t[18]:=57.0;

x[19]:=96.38; y[19]:=97.15; t[19]:=56.8;

x[20]:=97.47; y[20]:=97.93; t[20]:=56.6;

x[21]:=98.40; y[21]:=98.44; t[21]:=56.5;

for i:=1 to 21 do

begin

lymbda12:=(18.7/104)*exp(-deltag12/(1.987*(t[i]+273.15)));

lymbda21:=(104/18.7)*exp(-deltag21/(1.987*(t[i]+273.15)));

slag1:=-ln(x[i]/100+lymbda12*(100-x[i])/100);

slag2:=lymbda12/(x[i]/100+lymbda12*(100-x[i])/100);

slag3:=lymbda21/((100-x[i])/100+lymbda21*x[i]/100);

gamma[1,i]:=exp(slag1+((100-x[i])/100)*(slag2-slag3));

slag1:=-ln((x[i]/100)*lymbda21+(100-x[i])/100);

slag2:=lymbda12/(x[i]/100+lymbda12*(100-x[i])/100);

slag3:=lymbda21/((100-x[i])/100+lymbda21*x[i]/100);

gamma[2,i]:=exp(slag1-(x[i]/100)*(slag2-slag3));

end;

writeln(' Равновесные данные АЦЕТОН-ВОДА');

writeln(' и соответствующие им коэффициенты активности');

writeln;

writeln('x, мол% y, мол% t, C gamma1 gamma2 ');

for i:=1 to 21 do

begin

writeln(x[i]:2:2,' ',y[i]:2:2,' ',t[i]:2:2,' ',gamma[1,i]:2:3)ж

end;

readln;

end.

2. Алгоритм и программа расчета коэффициентов активности в многокомпонентной смеси по уравнению NRTL.

а.) Алгоритм-блок-схема.

Ввод исходных данных:

g_ij,g_ji, X_i, X_j, _ij, T

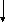
Расчет параметров уравнения NRTL:

G_ij,G_ji, _ij, _ji

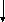
Вычисление коэффициентов актив-ности по уравнению (3)

(3)

-2-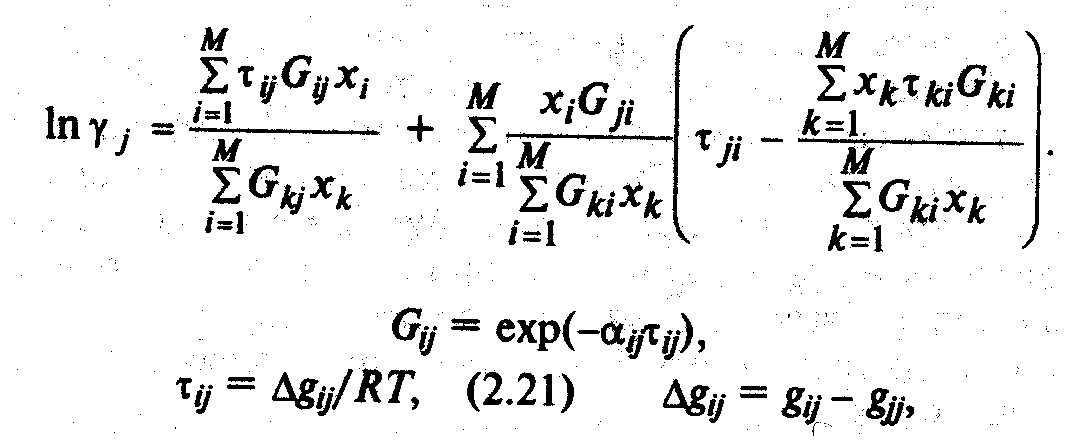

б.) Пример программы расчета коэффициентов активности по уравнению модели NRTL приведем для случая

бинарной пары ацетон-вода.

{Программа определения коэфиициентов активности

с использованием уравнения NRTL.}

uses crt;

var

G, tau : array [1..2,1..2] of real;

t1 : real;

x, y, t : array [1..21] of real;

C1, C2, C3, C4 : array [1..3] of real;

yir : array [1..21,1..2] of real;

gamma : array [1..2,1..21] of real;

ysum, deltag12, deltag21, shag12, shag21 : real;

r, rr, chis1, chis2, chis3, znam, slag2, temp, alfa : real;

k, i, j, z, n, l, f, p : integer;

lymbda12, lymbda21, Pi0, Pi1, nach, kon, rnew : real;

sum1, sum2, sum3, sum4, sum5, sum6, slag1 : real;

procedure poisk;

begin

ysum:=0;

r:=0;

rr:=0;

for f:=1 to 21 do

begin

temp:=t[f];

tau[1,1]:=0; tau[1,2]:=75.90/(1.987*(temp+273.15));

tau[2,1]:=1556.324/(1.987*(temp+273.15)); tau[2,2]:=0;

alfa:=0.2;

G[1,1]:=exp(-alfa*tau[1,1]); G[1,2]:=exp(-alfa*tau[1,2]);

G[2,1]:=exp(-alfa*tau[2,1]); G[2,2]:=exp(-alfa*tau[2,2]);

writeln(tau[2,1]:2:3);

writeln('G[1,1]=',G[1,1]:2:3,'; G[1,2]=',G[1,2]:2:3);

writeln('G[2,1]=',G[2,1]:2:3,'; G[2,2]=',G[2,2]:2:3);

readln;

for i:=1 to 2 do

begin

sum1:=0;

for j:=1 to 2 do

begin

if j=1 then

sum1:=sum1+tau[j,i]*G[j,i]*x[f]/100;

if j=2 then

sum1:=sum1+tau[j,i]*G[j,i]*(100-x[f])/100;

end;

sum2:=0;

for l:=1 to 2 do

begin

if l=1 then

sum2:=sum2+G[l,i]*x[f]/100;

if l=2 then

sum2:=sum2+G[l,i]*(100-x[f])/100;

end;

slag1:=sum1/sum2;

sum3:=0;

slag2:=0;

for j:=1 to 2 do

begin

if j=1 then

-3-

sum3:=sum3+x[f]*G[i,j]/100;

if j=2 then

sum3:=sum3+G[i,j]*(100-x[f])/100;

sum4:=0;

for l:=1 to 2 do

begin

if l=1 then

sum4:=sum4+G[l,j]*x[f]/100;

if l=2 then

sum4:=sum4+G[l,j]*(100-x[f])/100;

end;

sum5:=0;

for n:=1 to 2 do

begin

if n=1 then

sum5:=sum5+tau[n,j]*G[n,j]*x[f]/100;

if n=2 then

sum5:=sum5+tau[n,j]*G[n,j]*(100-x[f])/100;

end;

sum6:=0;

for l:=1 to 2 do

begin

if l=1 then

sum6:=sum6+G[l,j]*x[f]/100;

if l=2 then

sum6:=sum6+G[l,j]*(100-x[f])/100;

end;

slag2:=slag2+(sum3/sum4)*(tau[i,j]-sum5/sum6);

end;

gamma[i,f]:=exp(slag1+slag2);

end;

end;

end;

begin

{Массивы исходных равновесных данных}

x[1]:=1.15; y[1]:=27.91; t[1]:=92.0;

x[2]:=2.21; y[2]:=44.88; t[2]:=85.2;

x[3]:=6.38; y[3]:=68.09; t[3]:=72.1;

x[4]:=11.64; y[4]:=77.77; t[4]:=65.3;

x[5]:=17.27; y[5]:=80.73; t[5]:=62.7;

x[6]:=30.85; y[6]:=83.09; t[6]:=60.9;

x[7]:=44.39; y[7]:=84.21; t[7]:=60.3;

x[8]:=50.96; y[8]:=85.24; t[8]:=59.8;

x[9]:=52.28; y[9]:=85.12; t[9]:=59.8;

x[10]:=62.32; y[10]:=86.03; t[10]:=59.4;

x[11]:=68.29; y[11]:=87.23; t[11]:=58.8;

x[12]:=72.75; y[12]:=87.90; t[12]:=58.75;

x[13]:=76.29; y[13]:=88.71; t[13]:=58.35;

x[14]:=82.08; y[14]:=90.37; t[14]:=58.2;

x[15]:=86.55; y[15]:=92.08; t[15]:=57.7;

x[16]:=90.04; y[16]:=93.53; t[16]:=57.6;

x[17]:=92.37; y[17]:=94.72; t[17]:=57.7;

x[18]:=93.83; y[18]:=95.62; t[18]:=57.0;

x[19]:=96.38; y[19]:=97.15; t[19]:=56.8;

x[20]:=97.47; y[20]:=97.93; t[20]:=56.6;

x[21]:=98.40; y[21]:=98.44; t[21]:=56.5;

C1[1]:=0.3461307*100; C2[1]:=-0.4873446*10000; C3[1]:=-0.3249502E-8;

C1[3]:=0.5070924*100; C2[3]:=-0.6784604*10000; C3[3]:=-0.1042392E-8;

-4-

C1[2]:=0.3079802*100; C2[2]:=-0.5966069*10000; C3[2]:=0.1030134E-8;

C4[1]:=-0.3422*10;

C4[3]:=-0.5360*10;

C4[2]:=-0.2500*10;

poisk;

writeln(' Равновесные данные АЦЕТОН-ВОДА');

writeln(' и соответствующие им коэффициенты активности');

writeln;

writeln('x, мол% y, мол% t, C gamma1 gamma2 ');

for i:=1 to 21 do

writeln(x[i]:2:2,' ',y[i]:2:2,' ',t[i]:2:2,' ',gamma[1,i]:2:3);

readln;

end.

3. Алгоритм и программа расчета параметров модели NRTL, где в качестве минимизируемой функции взята

(4)

В формуле (4) N – число экспериментальных точек для рассматриваемой бинарной смеси;

Концентрация в паровой фазе рассчитывается по выражению:

y_i = _iP_i⁰x_i/P, (5)

где _i – коэффициент активности первого компонента в бинарной смеси;

P – общее давление (атм);

P_i⁰ – давление чистого первого компонента бинарной смеси как функции температуры:

P_i⁰=exp(C₁ⁱ + C₂ⁱ/T + C₃ⁱT + C₄ⁱlnT).

Ввод исходных данных:

g_ij,g_ji, X_i, X_j, _ij, T, N, h

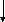
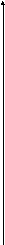
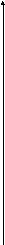
k=k+1

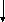
Расчет параметров модели NRTL

G_ij,G_ji, _ij, _ji

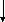
Вычисление коэффициентов актив-ности по уравнению (3)

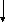
Расчет P_i⁰

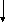
Расчет состава пара y_i^P

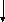
R=R+[(y_i^P-y_i^Э)² + (Т_i^P-T_i^Э)²]

-5-

k=N нет

да

R<R_min нет

да

R_min =R

k=0, g_ij=g_ij+h, g_ji=g_ji+h

Вывод полученных результатов

g_ij=g_ij-h, g_ji=g_ji-h

б.) Программа расчета параметров модели NRTL на примере бинарной пары ацетон-вода.

{Программа поиска параметров deltaG(ацетон-вода) и deltaG(вода-ацетон)

с использованием уравнения NRTL.}

uses crt;

var

G, tau : array [1..2,1..2] of real;

t1 : real;

x, y, t : array [1..21] of real;

C1, C2, C3, C4 : array [1..3] of real;

yir : array [1..21,1..2] of real;

gamma : array [1..2] of real;

ysum, deltag12, deltag21, shag12, shag21 : real;

r, rr, chis1, chis2, chis3, znam, slag2, temp, alfa : real;

k, i, j, z, n, l, f, p : integer;

lymbda12, lymbda21, Pi0, Pi1, nach, kon, rnew : real;

sum1, sum2, sum3, sum4, sum5, sum6, slag1 : real;

procedure poisk;

begin

ysum:=0;

r:=0;

rr:=0;

for f:=1 to 21 do

begin

temp:=t[f];

tau[1,1]:=0; tau[1,2]:=deltag12/(1.987*(temp+273.15));

tau[2,1]:=deltag21/(1.987*(temp+273.15)); tau[2,2]:=0;

alfa:=0.2;

-6-

G[1,1]:=exp(-alfa*tau[1,1]); G[1,2]:=exp(-alfa*tau[1,2]);

G[2,1]:=exp(-alfa*tau[2,1]); G[2,2]:=exp(-alfa*tau[2,2]);

writeln(tau[2,1]:2:3);

writeln('G[1,1]=',G[1,1]:2:3,'; G[1,2]=',G[1,2]:2:3);

writeln('G[2,1]=',G[2,1]:2:3,'; G[2,2]=',G[2,2]:2:3);

readln;

for i:=p to p do

begin

sum1:=0;

for j:=1 to 2 do

begin

if j=1 then

sum1:=sum1+tau[j,i]*G[j,i]*x[f]/100;

if j=2 then

sum1:=sum1+tau[j,i]*G[j,i]*(100-x[f])/100;

end;

sum2:=0;

for l:=1 to 2 do

begin

if l=1 then

sum2:=sum2+G[l,i]*x[f]/100;

if l=2 then

sum2:=sum2+G[l,i]*(100-x[f])/100;

end;

slag1:=sum1/sum2;

sum3:=0;

slag2:=0;

for j:=1 to 2 do

begin

if j=1 then

sum3:=sum3+x[f]*G[i,j]/100;

if j=2 then

sum3:=sum3+G[i,j]*(100-x[f])/100;

sum4:=0;

for l:=1 to 2 do

begin

if l=1 then

sum4:=sum4+G[l,j]*x[f]/100;

if l=2 then

sum4:=sum4+G[l,j]*(100-x[f])/100;

end;

sum5:=0;

for n:=1 to 2 do

begin

if n=1 then

sum5:=sum5+tau[n,j]*G[n,j]*x[f]/100;

if n=2 then

sum5:=sum5+tau[n,j]*G[n,j]*(100-x[f])/100;

end;

sum6:=0;

for l:=1 to 2 do

begin

if l=1 then

sum6:=sum6+G[l,j]*x[f]/100;

if l=2 then

sum6:=sum6+G[l,j]*(100-x[f])/100;

end;

slag2:=slag2+(sum3/sum4)*(tau[i,j]-sum5/sum6);

end;

-7-

gamma[i]:=exp(slag1+slag2);

Pi0:=exp(C1[i]+C2[i]/(t[f]+273.15)+C3[i]*(t[f]+273.15)+C4[i]*ln(t[f]+273.15

if i=1 then

ysum:=ysum+gamma[i]*Pi0*x[f]/100;

if i=2 then

ysum:=ysum+gamma[i]*Pi0*(100-x[f])/100;

end;

if p=1 then

r:=r+sqr(y[f]/100-ysum);

if p=2 then

r:=r+[sqr((100-y[f])/100-ysum)+sqr(t[f]-tr)];

end;

end;

begin

{Массивы исходных равновесных данных}

x[1]:=1.15; y[1]:=27.91; t[1]:=92.0;

x[2]:=2.21; y[2]:=44.88; t[2]:=85.2;

x[3]:=6.38; y[3]:=68.09; t[3]:=72.1;

x[4]:=11.64; y[4]:=77.77; t[4]:=65.3;

x[5]:=17.27; y[5]:=80.73; t[5]:=62.7;

x[6]:=30.85; y[6]:=83.09; t[6]:=60.9;

x[7]:=44.39; y[7]:=84.21; t[7]:=60.3;

x[8]:=50.96; y[8]:=85.24; t[8]:=59.8;

x[9]:=52.28; y[9]:=85.12; t[9]:=59.8;

x[10]:=62.32; y[10]:=86.03; t[10]:=59.4;

x[11]:=68.29; y[11]:=87.23; t[11]:=58.8;

x[12]:=72.75; y[12]:=87.90; t[12]:=58.75;

x[13]:=76.29; y[13]:=88.71; t[13]:=58.35;

x[14]:=82.08; y[14]:=90.37; t[14]:=58.2;

x[15]:=86.55; y[15]:=92.08; t[15]:=57.7;

x[16]:=90.04; y[16]:=93.53; t[16]:=57.6;

x[17]:=92.37; y[17]:=94.72; t[17]:=57.7;

x[18]:=93.83; y[18]:=95.62; t[18]:=57.0;

x[19]:=96.38; y[19]:=97.15; t[19]:=56.8;

x[20]:=97.47; y[20]:=97.93; t[20]:=56.6;

x[21]:=98.40; y[21]:=98.44; t[21]:=56.5;

C1[1]:=0.3461307*100; C2[1]:=-0.4873446*10000; C3[1]:=-0.3249502E-8;

C1[3]:=0.5070924*100; C2[3]:=-0.6784604*10000; C3[3]:=-0.1042392E-8;

C1[2]:=0.3079802*100; C2[2]:=-0.5966069*10000; C3[2]:=0.1030134E-8;

C4[1]:=-0.3422*10;

C4[3]:=-0.5360*10;

C4[2]:=-0.2500*10;

for p:=1 to 2 do

begin

if p=1 then

writeln('Поиск параметров для ацетона');

if p=2 then

writeln('Поиск параметров для воды');

writeln('Введите начальные значения для параметров:');

write('Для deltaG(ацетон-вода): '); read(nach);

write('Для deltaG(вода-ацетон): '); read(kon);

deltag12:=nach;

deltag21:=kon;

{Начальный шаг}

shag12:=1;

shag21:=1;

poisk;

-8-

writeln('R0=',r:2:3);

rnew:=r;

repeat

rr:=rnew;

r:=0;

k:=0;

while (r<rnew) do

begin

k:=k+1;

if k>1 then

rnew:=r;

deltag12:=deltag12+shag12;

poisk;

end;

writeln('Выход из 1-го цикла.');

writeln('rnew=',rnew:2:5);

readln;

r:=0;

n:=0;

deltag12:=deltag12-shag12;

{writeln('r=',r:2:10);}

while (r<rnew) do

begin

n:=n+1;

if n>1 then

rnew:=r;

deltag21:=deltag21+shag21;

poisk;

end;

writeln('Выход из 2-го цикла.');

writeln('rnew=',rnew:2:5);

deltag21:=deltag21-shag21;

writeln('deltag12=',deltag12:2:5,'; deltag21=',deltag21:2:5);

readln;

z:=z+1;

write('Процесс идет!!! ',z);

clrscr;

if k=1 then

write('Введите другой шаг: ');

read(shag12);

if n=1 then

write('Введите другой шаг: '); read(shag21);

until (rnew<0.001);

writeln('Минимум R=',r:2:3);

writeln('deltag12=',deltag12:2:3);

writeln('deltag21=',deltag21:2:3);

end;

end.

-9-

4. Алгоритмы и программы расчета равновесных составов и температуры кипения бинарных и многокомпонен-тных смсей для моделей Вильсона и NRTL.

4.1 Уравнение Вильсона.

а.) Алгоритм расчета равновесных составов и температуры кипения по уравнению Вильсона.