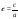shpor_po_matematike_FEB_1-kurs
.docx-
 6
егер :А)
6
егер :А)

-
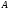 9
аталады. -осы
оқиғалардың көбейтіндісі
9
аталады. -осы
оқиғалардың көбейтіндісі -
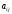 8
байланыс:А)
8
байланыс:А)

-
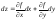 1
бойынша :
А)
1
бойынша :
А)
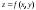 функциясының
толық дифференциалы есептелінеді
функциясының
толық дифференциалы есептелінеді -
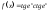 2
табыңыз: -
2
табыңыз: -
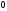
-
 2
табыңыз: -
2
табыңыз: -
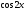
-
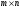 7
егер …A)
7
егер …A)
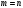
-
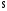 8
атайды?А) кездейсоқ
8
атайды?А) кездейсоқ -
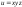 4
керек:A)
4
керек:A)
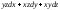
-
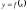 2
көрсетіңіз:A)
2
көрсетіңіз:A)
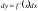
-
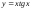 2
табыңыз -
2
табыңыз -
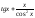
-
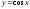 2
табыңыз:A)
2
табыңыз:A)
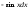
-
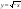 4
керек: -
4
керек: -
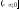
-
 5
керек: -
5
керек: -
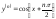
-
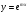 5
керек:А)
5
керек:А)

-
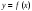 6
анықталады? -
6
анықталады? -
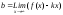
-
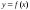 6
анықталады? A)
6
анықталады? A)
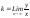
-
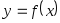 4
егер :A)
4
егер :A)
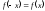
-
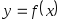 4
егер :A)
4
егер :A)

-
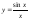 2
табыңыз:A)
2
табыңыз:A)
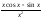
-
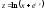 3
табыңыз:A)
3
табыңыз:A)
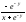
-
 4
4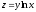 :A)
:A)
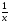
-
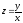 5
керек:A)
5
керек:A)
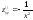
-
0 :A)
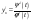
-
0: A)
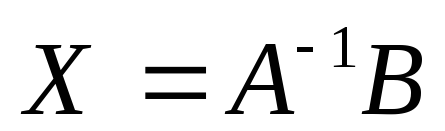
-
0:.A) Функцияның күдікті нүктелері
-
00 -
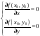
-
000: A)
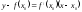
-
0000: A)
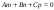
-
0000:A)
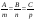
-
0000:A)
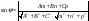
-
00000 :A)
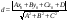
-
01 -
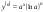
-
01:A)
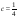
-
012 A)
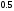
-
012: A)
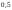
-
021010: A)
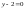
-
0212:A)

-
02312:A)
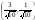
-
025234 -

-
03: A)

-
035:A)
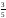
-
042: A)

-
0515 -
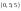
-
05473 A)
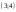
-
0708: А) 0,38
-
08: A)
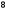
-
1.A)
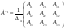
-
1:A)
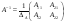
-
10 -

-
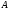 10
атайды.
-
10
атайды.
- және
және
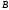 оқиғаларының қосындысы
оқиғаларының қосындысы -
1000500000200011: А)
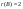
-
101827: А) 0,56
-
102 -
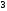
-
104031 - 4
-
1042: А)
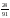
-
11 -
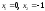
-
110 :A)
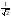
-
11010:A)
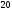
-
11112222 -
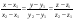
-
1112220: A)
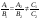
-
1122 -
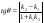
-
1122 А)
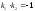
-
1122322233230:A)
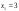
-
11249: А)
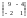
-
113: А)
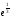
-
11733.А)
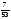
-
12: А)
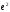
-
12:А)
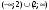
-
120 -
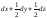
-
12023: А) 0,65
-
12025: А) 0,6
-
120303526:A)
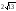
-
1203411: A) көбейтуге болмайды
-
1210 -
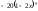
-
121034225:A)
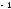
-
12113256:A)
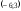
-
1212: А)
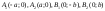
-
12132: А)
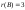
-
1221:A)
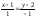
-
122200 -
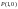
-
122234012:A)
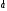 и
и
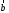
-
12231: A)

-
123 -
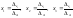
-
123025003:A)
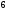
-
1231:A)
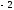
-
123101061. А)
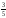
-
123123 -
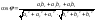
-
123123:А)
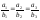
-
12322: A)
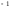
-
123231:A)
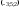
-
12335435 -
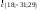
-
1234122330212316: А)
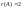 ,
,
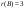
-
12345678923:A) -6
-
123623163126: А)
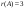
-
12896. А) 112
-
13: A)
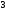
-
13112230120:A)
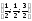
-
13223021233031514301172430:.А)

-
132231192633132431: А)

-
134023121А)
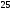
-
1410:A)
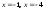
-
142 -
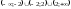
-
14563670:A)
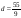
-
15103: А)
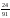
-
151053: А) 1200
-
15243121102833311521235:.А)үйлесімсіз
-
15243341212234051328341: А)
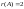
-
1552: А)
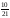
-
162200 -
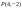
-
162252400: А)
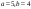
-
165:A)

-
2:
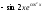
-
2: A)
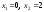
-
2:А)
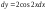
-
201:A)
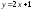
-
21 -
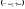
-
21028:А)
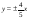
-
21141034:A)
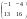
-
212 – максимумы жоқ
-
212234576 :А)
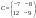
-
21235:A)
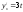
-
21235346:A)
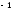
-
213 -
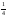
-
213212362335:A)
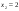
-
2136:A)

-
216241:А)

-
22 - 1.
-
22А)
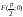
-
22:A)
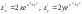
-
22:A)
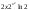
-
22:А)
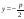
-
221 – көлбеу асимптотасы жоқ
-
2211212. А)
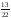
-
22121:А)
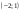
-
221321: A)
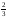
-
222:A)
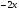
-
22222 -
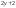
-
22222000 А) шеңбердің теңдеуі
-
22232238: A)
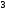
-
2231:A)
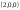
-
223152: A)
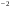
-
22322111 -
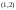
-
224.А)
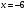
-
224800 -
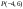
-
2252161:А)
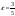
-
2253032420:A)
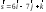
-
2310: A)
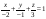
-
231023 -
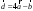
-
2313 -
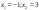
-
2325: A)
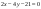
-
232542 -
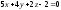
-
2332:A)

-
234473122:A)
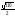
-
235 -

-
2352 -
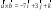
-
235260 -
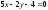
-
23540 :A)
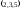
-
236:A)
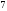
-
2362152511 -
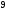
-
237357 -
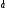 и
и
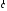
-
2431 -
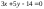
-
25:A)
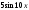
-
25:А)
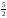 .
. -
2520:.А)
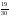
-
2530143123232:A)8
-
254367 -
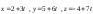
-
261:А)
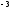
-
262 -
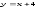
-
262:A)
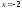
-
27343621 -
 и
и
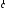
-
28232622 A)

-
292:A)
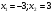
-
30:A)
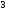
-
3010515:А)
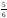
-
31:A)
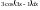
-
31045035тап.А) 0,80
-
31103031: А)
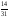
-
3122:A)
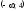
-
3134:A)
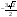
-
31617242230 -
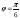
-
32 -
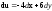
-
32 -
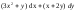
-
321:A)
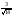
-
32111:A)
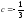
-
322:A)
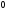
-
322121: A)

-
3222512 -
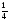
-
3223:A)
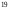
-
324:A)
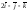
-
325: А) 0,8
-
325:A)
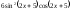
-
325617 -
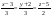
-
32752A)

-
328 A)
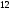
-
32923: A)

-
33:A)

-
33:A)

-
33:A)
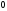
-
331 -
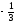
-
33251:A)
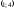
-
3326:А)
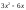
-
332914:A)
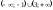
-
333:A)
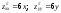
-
3411562827:A)

-
34120:A)

-
34203470 -
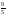
-
34232 -
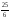
-
345 -
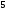
-
34512045311:A) -6
-
35 -

-
35 –бос жиын
-
3552: А) 6.
-
357123135.А)
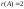
-
362452 -
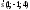
-
4 -
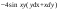
-
4121030122302132430:.А)
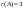
-
42:A)
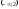 .
. -
422522:A)

-
422522:A)

-
4231 -
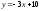
-
423230224143 -
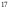
-
432:А)
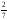
-
43235:A)
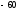
-
43323232: A)
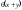
-
44: А)24
-
451312:А)
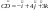
-
45822331:А)
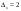
-
463526443432 -
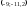
-
47: А)
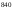
-
510105:.А)
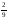
-
5110412230 -
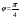
-
52:A)
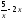
-
532.А)
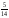
-
5420:A)
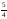
-
554 -

-
561241 -
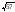
-
621
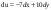
-
635435 -
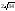
-
64: А)
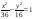
-
647: А) 60
-
72 А)
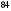
-
7211 -
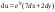
-
9: А)504
-
912110:A)
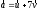
-
9228:A)
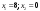
-
А 21 атайды?А) А оқиғасының ықтималдығы
-
Алг 7 онда :А) Біртекті деп аталады
-
Аны 2 егер :А) қандайда бір жол (баған) элементтерінің ортақ көбейткішін анықтауыш белгісінің алдына шығарса
-
Аны 3 егер :А) екі жолдың (бағанның) сәйкес элементтері пропорционал болса
-
Бұр 3 теңдеуі:А)
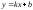
-
Бір 6 егер:А)
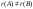
-
Бір 7 егер:А)
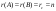
-
Бір 8 егер: А)
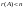
-
Бір 8 егер:А)
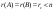
-
Бір 9 аталады.А) компланар
-
Бір 9 шарты:А)
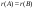
-
Гип 1 теңдеуі :А)

-
Гип 2 көрінісі:А)
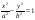
-
Еге 11 атаймыз?А) мүмкін емес
-
Еге 12 атаймыз?А) ақиқат
-
Еге 21 табылады A)
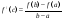
-
Еге 22 табылады :A)
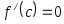 .
. -
Еге 8 теңдеуі :А)
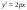
-
Еге 8 теңдеуі :А)
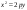
-
Екі 10 тап. А)
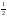
-
Екі 12 керек. А)
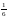
-
Екі 15 керек. А)
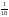
-
Екі 22 керек.А)
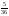
-
Екі 3 егер...А) екі матрицаның да жолдары мен бағандарының саны сәйкесінше тең болса
-
Екі 3 тең? А)

-
Екі 5 формуласы:А)
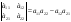
-
Екі 5 шарты:A)
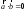
-
Екі 6 егер :А) бірінші матрицаның бағандарының саны екінші матрицаның жолдарының санына тең болса
-
Екі 8 атайды?А) үйлесімсіз
-
Екі 9 тап.А)
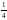
-
Ква 4 егер A) бас диагональдан басқа элементтері нөлге тең болса
-
Кең 3 көрсетіңіз :A)
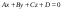
-
Кең 3 көрсетіңіз :A)
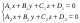
-
Кең 5 формуласы:А)
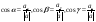
-
Кең 6 көрінісі:А)
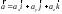
-
Кең 8 көрсетіңіз :A)
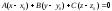
-
Қар 5 тең? А)

-
Мат 2 көбейтіледі A) матрицаның барлық элементі сол санға
-
Мат 10 аталады. А) матрицаның k-ретті миноры
-
Мат 2 айтамыз.А) матрица минорының нөлге тең емес ең үлкен ретін
-
Мат 2 егер :А) матрица жолының (бағанының) элементтерін нөлден өзгеше санға көбейтсе
-
Мат 3 егер: А) матрица рангілері тең болса
-
Нөл 8
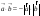 :
А)
:
А)
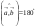
-
Оқу 22 тап. А)
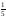
-
Сыз 6 егер: А) ең болмағанда бір шешімі болса
-
Сыз 7 егер ... А) жүйенің анықтауышы нөлден өзгеше болса
-
Сыз 7 қолданылады? А) САТЖ-ін Гаусс әдісімен шешуде
-
Сын 12 атайды? А) жалғыз ғана мүмкіндікті оқиға
-
Үйл 9 аталады.А) Анықталған
-
Фун 9 аталады? А) Иілу нүктесі
-
Элл 2 көрінісі :А)
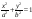
-
Элл 4 формуласы:А)