
Конспект Математическое моделирование. Автор: профессор МГОТУ Вилисов В.Я
.pdf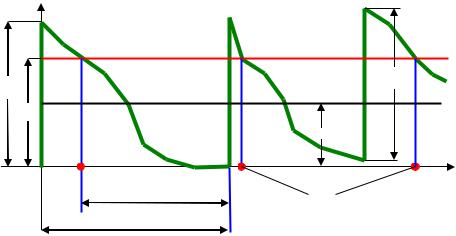
При стоимостной значимости учитывается стоимость запасов, как замороженных оборотных средств. При этом для уменьшения этого объема средств обычно используют следующие приемы:
1.Методика 20/80. Она отражает тот статистический факт, что обычно 20% материалов составляют 80% стоимости запасов. Предлагается эту группу отслеживать и своевременно заказывать ее пополнение.
2.Методика АВС (Парето). Здесь весь объем запасов по степени важности делится на три группы:
А: 10% объема, 65% стоимости;
В: 25% объема, 25% стоимости;
С: 65% объема, 10% стоимости.
Технологическая значимость запасов может не совпадать с классификацией запасов по этим двум методикам. Так в производстве дешевая деталь может задержать выпуск дорогого продукта.
Существуют специальные современные организационные технологии, обеспечивающие минимизацию запасов, например:
Точно вовремя (Система Тойота).
Канбан.
Управление цепочками поставок.
Задача управления запасами: Определить оптимальные объемы и моменты времени заказа множества ресурсов, обеспечивающих эффективное функционирование зависящих от них бизнес-процессов.
Часто задачу управления запасами множества ресурсов можно рассматривать как множество задач управления одним ресурсом. Исключение составляют те случаи, когда ресурсы конкурируют за ограниченное место на складе и/или за ограниченные финансовые средства на закупку.
Далее рассмотрим некоторые модели управления запасами одного ресурса.
3.2. Процесс расходования и пополнения запасов
Количество расходуемых запасов является случайным процессом. Реализация этого процесса может иметь такой вид.
Q |
|
Q |
|
|
|
|
R |
|
|
|
Средний запас |
|
Время |
|
|
выполнения заказа |
Точки заказа |
|
|
|
|
Продолжительность цикла |
|
Здесь:
Q – объем заказа;
T – продолжительность одного цикла (периода планирования);
d – интенсивность спроса на ресурс (количество, потребляемое в единицу времени); D – спрос на ресурс за один цикл;
K – издержки оформления (размещения) заказа;
h – интенсивность издержек хранения на единицу ресурса (удельные издержки хранения), т.е. стоимость хранения единицы ресурса в единицу времени;
H – все издержки хранения партии товара за один цикл.
21
Факторы процесса, влияющие на тип модели оптимального управления запасами:
Характер параметров процесса – стационарный, нестационарный.
Характер спроса - детерминированный или случайный.
Время выполнения заказа – фиксированное, случайное, не учитывается (не значимо).
Издержки оформления заказа – учитываются, не учитываются.
Издержки дефицита ресурса – учитываются, не учитываются (т.е. дефицит не допустим).
Скидки от объема заказа – нет, есть (могут быть линейными или кусочнопостоянными).
Источник поставки – внешний, внутренний (свое производство).
Количество планируемых ресурсов – один, много (при ограниченном складе или финансовых средствах).
3.3. Модель с постоянным спросом
Цель планирования – определить объем заказа Q и периодичность (цикл) заказа T. Предпосылки модели:
Интенсивность спроса на ресурс (d) не изменяется во времени.
Заказ выполняется мгновенно.
Дефицит не допускается (или плата за него велика).
Дано:
Издержки размещения заказа K.
Удельные издержки хранения h.
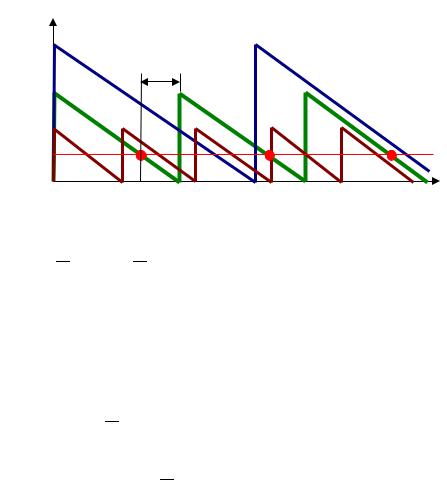
Для этой модели все циклы расходования/заказа идентичны:
Уровень запасов
Q3
τ
Q2
Q1
T1 Tзак T2 T3 t
Наклоны расходования ресурса для всех возможных вариантов «пилы» одинаковы, т.к. определяются интенсивностью спроса (d):
d QT или T Qd или Q Td .
Поскольку процесс стационарный, то целевую функцию (ЦФ), как функцию объема партии заказа Q , можно сформировать для произвольной единицы времени. Для этого
сначала определим издержки за один цикл. Издержки размещения за один цикл:
S1 K .
Издержки хранения за один цикл:
S2 H h Q2 T
Общие издержки:
S S1 S2 K h Q2 T
22
Интенсивность общих издержек (с учетом T Qd ):
s(Q) s1 s2 TS KT hQ2 KdQ hQ2 .
Задача оптимизации заключается в том, чтобы найти такой размер партии заказа Q ,
чтобы минимизировать интенсивность общих издержек s (критерий – минимум общих издержек):
Qopt arg min s(Q)
Q
Необходимое условие оптимальности:
|
s |
|
|
Kd |
|
h |
0 , откуда получим формулу экономичного размера заказа Уилсона: |
||||||
|
Q |
Q2 |
|
||||||||||
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
Q |
|
|
2Kd |
. |
|
|
|||||||
|
|
|
|
|
|||||||||
|
opt |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда T |
|
|
|
Qopt |
. |
||||||||
|
|
|
|||||||||||
|
|
|
opt |
|
|
|
|
|
d |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
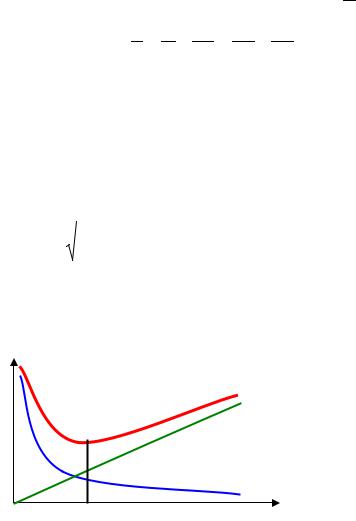
Графически две учтенные составляющие издержек имеют вид:
s(Q)
s
s2
s1
Q
Qopt
Учет срока выполнения заказа.
На практике срок поставки не может быть мгновенным. Пусть он известен и равен , причемTopt . Но при известной интенсивности спроса d можно вычислить тот критический
уровень запаса Qзак , при достижении которого следует делать заказ, чтобы он пришел к моменту полного окончания запаса:
Qзак d ,
Tзак Topt .
3.4. Модель со скидками
Предпосылки те же, что и в Модели с постоянным спросом. Дополнительное условие: ресурс (для пополнения запасов) может быть приобретен со скидкой, если объем заказа Q превышает порог q. Это условие добавляет в число издержек (в целевую функцию) и стоимость приобретаемой партии ресурса. Скидка по цене имеет вид:
c , если Q q
c c1 , если Q q , где c1 c2 .
2
Тогда составляющая интенсивности издержек на приобретение ресурса:
23
|
c1Q |
|||
|
|
|
|
|
|
T |
|||
|
|
|||
s3 |
|
|
|
|
|
|
|
||
|
|
c2Q |
|
|
T
|
c1Q |
c1d , если Q q |
||||
Q |
||||||
|
|
|||||
|
|
|
|
|
||
|
|
|
||||
|
d |
. |
||||
|
c2Q |
|||||
|
c2 d , если Q q |
|||||
Q |
||||||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
|
||||
Тогда полная интенсивность издержек с учетом скидок:
s1 |
(Q) c d |
Kd |
|
|
hQ |
, если Q q |
||||
|
|
|
|
|||||||
|
1 |
|
|
Q |
2 |
|
|
|||
|
|
|
|
|
|
|||||
s(Q) |
|
|
|
Kd |
|
|
|
hQ |
|
|
s 2 |
(Q) c |
d |
|
|
|
, если Q q |
||||
|
|
|
|
|||||||
|
2 |
|
|
Q |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Т.к. s1 (Q) |
отличается от s 2 (Q) на постоянную величину (не зависящую от переменной Q |
|||||||||
), то координаты их минимумов совпадут и составят, как и в предыдущей модели, величину:
2Kd Qm  h .
h .
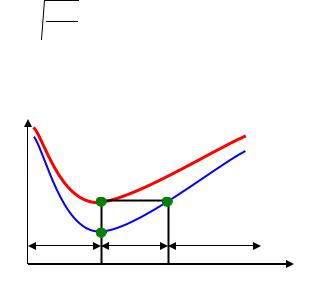
Однако для общих издержек s(Q) оптимальный объем заказа зависит от конкретного значения порога q.
s(Q)
s1
s2
I1 |
I2 |
I3 |
Q
Qm R
Для выбора оптимального объема партии заказа важно знать, на каком интервале находится точка разрыва цены q – на I1, I2 или I3. Рассмотрим эти варианты.
Точка R определяется из равенства:
s1 (Q ) s 2 (R) , или |
|
|
|
|
|||||||
|
|
m |
|
|
|
|
|
|
|
|
|
c |
d |
Kd |
|
hR |
s1 (Q ) , откуда |
|
|||||
|
|
|
|
||||||||
2 |
|
|
|
R |
2 |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
2(c2 d s1 (Qm )) |
|
2Kd |
|
|
||||
R |
|
|
|
|
|
|
|
|
|
0 . |
(*) |
|
|
|
|
|
h |
R |
h |
||||
|
|
|
|
|
|
|
|
|
|||
Решив это квадратное уравнение относительно R, найдем границу между зонами I2 и I3 (как максимальное, т.е. расположенное правее, из двух решений). Анализ трѐх вариантов расположения границы q показывает, что оптимальный объем заказа имеет такой вид:
|
Q |
m |
, если q I |
1 |
или q I |
3 . |
Qopt |
|
|
|
|||
|
q, |
если q I 2 |
|
|
||
Покажем это на графиках.
24
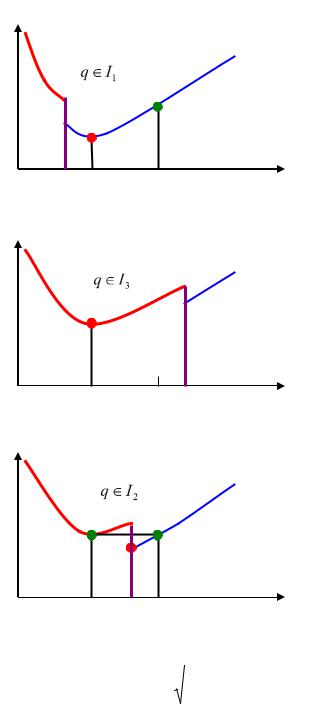
s(Q)
s1
s2
Q
q Qm |
R |
s(Q)
s1
s2
Q
Qm |
R q |
s(Q)
s1
s2
Q
Qm q R
Алгоритм вычисления оптимальной партии заказа для данной модели состоит из двух этапов:
Этап 1. Вычислить Q |
|
|
|
2Kd |
|
. Если q I |
|
, то Q |
Q , иначе выполнить этап 2. |
|
m |
|
1 |
|
|||||||
|
|
|
h |
opt |
m |
|
||||
|
|
|
|
|
|
|
|
|||
Этап 2. Найти границу R зон I2, I3 из квадратного уравнения (*). Если q I 2 , то Qopt |
q , |
|||||||||
иначе (при q I3 ) - Qopt Qm .
3.5. Модель с дефицитом
В некоторых случаях допустим дефицит ресурса.
Для моделирования таких ситуаций в исходную модель с постоянным спросом включаются и потери от дефицита. При этом процесс расходования-пополнения запасов имеет вид:
25

Уровень запасов
Q E
t
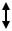 F TF T
F TF T
F – допустимый уровень дефицита – это неудовлетворенный спрос или отрицательный запас. При этом предполагается, что с приходом очередной партии ресурса дефицит мгновенно погашается и дефицитный объем не хранится на складе;
b – издержки от дефицита единицы ресурса в единицу времени.
Интенсивности издержек следующие (с учетом T Qd ):
издержки заказа: s1 KT KdQ ;
издержки хранения складываются из затрат на хранение объема (Q-F) в течении
времени |
TF: s2 h |
(Q F )TF |
. Учитывая, из подобия |
треугольников, что |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
2T |
|
|
|
|
|
|
|
|
Q |
|
T |
|
|
|
|
(Q F )T |
. С учетом этого: s |
|
h |
(Q F )2 |
||
|
|
|
, получим: T |
F |
|
|
2 |
|
. |
|||||
Q F |
|
|
|
|
||||||||||
|
TF |
|
|
|
|
Q |
|
|
2Q |
|||||
|
|
|
|
|
|
|
|
|
||||||
издержки дефицита определяются аналогично издержкам хранения: s4 b F 2 .
2Q
Общие издержки:
|
|
|
|
|
Kd |
|
h(Q F )2 |
bF 2 |
||
s s s |
2 |
s |
4 |
|
|
|
|
|
|
. |
|
|
|
||||||||
1 |
|
|
Q |
|
2Q |
2Q |
||||
|
|
|
|
|
|
|||||
Эта ЦФ имеет экстремумы по Q и по F. Рассмотрим два варианта поиска решения:
1.Оптимальный объем заказа при фиксированном уровне дефицита F.
2.Пару оптимальных параметров – объем заказа и уровень дефицита. Вариант 1. Необходимое условие оптимальности по Q:
|
s |
|
|
|
|
Kd |
|
|
|
h |
|
|
|
hF 2 |
|
|
|
bF 2 |
0 , |
|||||||
|
Q |
|
|
Q2 |
|
2 |
|
|
2Q2 |
|
2Q2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Q2 |
|
2Kd |
|
|
(b h)F 2 |
, |
|
|
|
|
(**) |
|||||||||||||||
|
h |
|
|
|
|
|
|
h |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Q F |
|
|
|
|
2Kd |
|
|
|
|
(b h)F |
2 |
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
opt |
|
|
|
|
h |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вариант 2. Необходимое условие включает одновременно условие Варианта 1 и следующее условие:
s |
h |
2hF |
|
2bF |
0 , |
|
F |
2Q |
2Q |
||||
|
|
|
откуда:
F h Q , b h
26
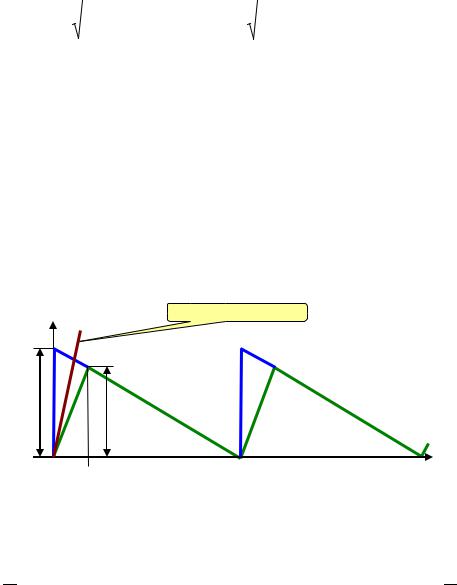
подставив его в (**) и выполнив преобразования, получим:
Q2 |
2Kd |
|
b h |
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
h |
b |
|
|
|
|
|
|
|||||||
И окончательно: |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Q |
|
2Kd |
|
b h |
; |
F |
2Kd |
|
h |
|
||||||
opt |
|
h |
|
b |
opt |
b |
b h |
|
||||||||
|
|
|
|
|
|
|
||||||||||
Отсюда максимальный размер запаса (или максимальная потребная емкость склада):
Emax Qopt Fopt .
3.6. Модель с производством (с постепенным пополнением запасов)
В тех случаях, когда запас восполняется не мгновенно, а с некоторой интенсивностью
(единиц ресурса в единицу времени), потребная емкость склада может быть снижена за счет того, что параллельно протекают два процесса – пополнение (в течении времени Тпост) и непрерывное потребление. В крайнем случае склад не нужен, когда эти процессы имеют равную интенсивность.
Этот тип модели описывает и ситуации, в которых на том же предприятии есть производство, выпускающее ресурс. При этом затраты на оформление заказа (К) имеют другое содержание – затраты на переналадку оборудования и/или подготовку производства для изготовления заказанной партии.
Уровень запасов |
Линия поставки |
Q
E
t
Tпост |
T |
Издержки размещения (и/или переналадки) за один цикл:
S1 K .
Издержки хранения за один цикл можно найти из геометрических построений. В исходной задаче (с постоянным спросом) объем ресурса, хранимого за один период равен
Q2 T . В рассматриваемой задаче объем ресурса определится как E2 T .
Уравнения линии увеличения запасов (возрастающая часть «пилы» - т.е. поставки за вычетом потребления) и линии потребления (убывающая часть «пилы») имеют вид
соответственно: y ( d)t ,
y Q td ,
где, y - это ордината графиков, отражающая количество ресурса. Из этих уравнений можно найти координаты вершины «пилы»:
|
Q |
|
|
|
d |
|
|
d |
|
t |
|
T |
; |
y |
|
Q 1 |
|
|
Q E . |
|
|
|
|||||||
|
|
пост |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда издержки хранения:
|
|
|
E |
|
Q |
|
d |
||
S |
2 |
h |
|
T h |
|
1 |
|
|
T . |
|
|
|
|||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Общие издержки:
27
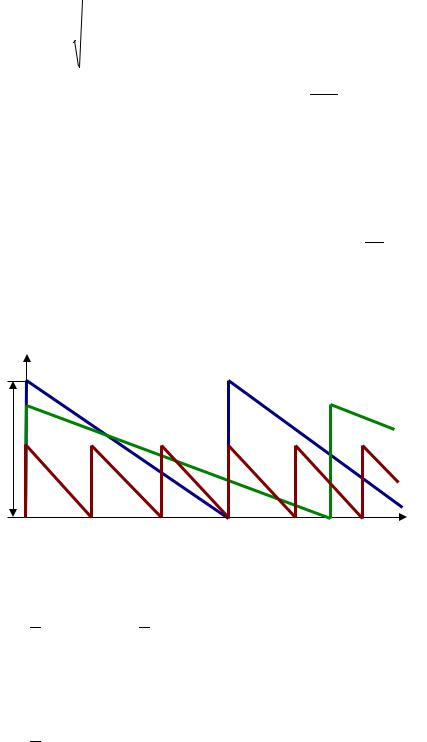
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
||||
S S |
1 |
S |
2 |
|
K h |
|
|
|
1 |
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Интенсивность общих издержек (с учетом T |
Q |
): |
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|||
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
K |
|
|
|
hQ |
|
|
d |
|
Kd |
|
hQ |
|
|
d |
||||||||||
s s s |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
T T |
|
|
2 |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||
Необходимое условие оптимальности: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
s |
|
|
|
Kd |
|
|
|
h |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 , откуда: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Q |
|
|
|
Q |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Qopt |
|
|
|
|
|
2Kd |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
h1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда период пополнения запасов: Topt Qopt . d
Максимальный объем запасов (потребный объем склада) получим, подставив оптимальный объем партии поставки в выражение для ординаты вершины «пилы»:
|
|
|
|
d |
|
|
E |
max |
1 |
|
|
Q . |
|
|
||||||
|
|
|
|
|
opt |
|
|
|
|
|
|
|
|
3.7. Многопродуктовая модель с ограниченным объемом склада
Рассмотрим случай нескольких продуктов ( i 1, n ), использующих общий склад. Для
каждого продукта процесс потребления-расходования аналогичен исходной модели. Дополнительными будут лишь параметры:
ai – необходимый объем (площадь) для хранения единицы i-го товара; А – доступный объем (площадь) для хранения всех продуктов. Уровень запасов
Q2
T1 |
T2 |
t |
T3 |
ЦФ суммарных издержек:
|
|
|
n |
K d |
h Q |
||||
|
|
|
|
i i |
|
i |
i |
|
|
L(Q) |
|
|
|
|
|
|
. |
||
|
|
|
i 1 |
|
Qi |
2 |
|
|
|
Тогда задача оптимизации имеет вид:
Qopt arg min L(Q) |
|
|
Q |
|
|
при ограничениях: |
|
|
n |
|
|
ai Qi A , |
|
|
i 1 |
|
|
где |
|
|
Q Q1 Q2 |
Qn T ; |
Qi 0 . |
28
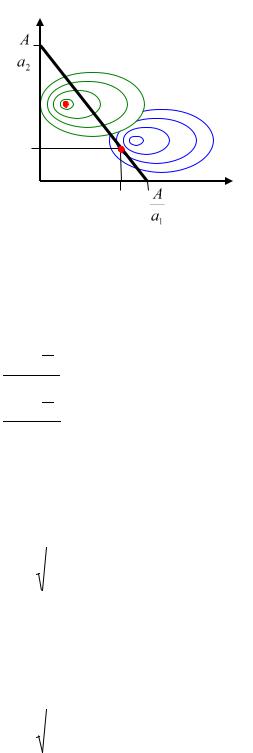
Данная задача относится к классу задач нелинейного программирования, где ЦФ нелинейна, а ограничения линейны. В этих задачах экстремум (решение) может достигаться как на границе ОДР, определяемой ограничениями, так и внутри нее. Например, для двумерного случая (n=2) ОДР и линии уровня ЦФ могут иметь вид, представленный на рисунке, где приведены два случая расположения экстремума – внутри ОДР (зеленые линии) и вне ОДР (синие линии). В первом случае решение совпадает с точкой экстремума ЦФ (красная точка). Во втором случае решение будет на границе ОДР, но не обязательно в еѐ крайней точке (красная точка на границе) и оно не совпадает с экстремумом ЦФ (оптимальные значения показаны на осях).
Q2
ОДР
Q2 opt
Q1
Q1 opt
Такую задачу можно решить одним из поисковых методов, например, средствами надстройки «Поиск решений» в Excel. Для общего случая можно воспользоваться методом множителей Лагранжа. Функция Лагранжа примет вид:
|
|
|
n |
K d |
h Q |
|
n |
|
|||
|
|
|
|
|
i i |
||||||
|
|
|
|
i i |
|
i i |
|
|
|||
L( ,Q) |
|
|
|
|
|
|
|
|
a Q |
||
|
|
|
i 1 |
Qi |
2 |
i 1 |
|
||||
Необходимое условие оптимальности:
A .
L( ,Q)
Qi
L( ,Q)
|
Ki di |
|
hi |
a |
|
0 |
|
i |
|
. |
|
|
i |
; |
1, n |
(***) |
|||||||||
Q2 |
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
ai Qi A 0 .
i 1n
Выразить из этой системы уравнений значения Qi даже для двух переменных
представляет собой громоздкую задачу. Поэтому конструктивной является процедура пошагового перебора значений . Она состоит из 3-х этапов:
Этап 1. Вычисляются оптимальные значения запасов по каждому продукту независимо без учѐта ограниченного объема склада по формуле Уилсона:
Q |
|
2Ki di |
|
, i |
|
. |
|
|
1, n |
||||||
|
|||||||
i |
hi |
||||||
|
|
||||||
Этап 2. Проверяется условие ограниченности объема склада для полученных значений запасов. Если условие выполняется, то полученные значения являются оптимальными. Если условие не выполняется, то необходимо выполнить этап 3.
Этап 3. Из первой группы необходимых условий оптимальности (***) получим параметрическое (от ) выражение оптимальных запасов по продуктам, аналогичное формуле Уилсона:
|
|
|
2Ki di |
|
|
|
|
|
|
Qi |
|
|
|
, i 1, n , |
|||||
hi |
2ai |
|
|
||||||
|
|
|
|
|
|
|
|||
откуда видно, что при 0 получим то же решение, что и для задачи без ограничений. Задача поиска решения сводится к пошаговому перебору параметра с одновременным расчетом значения ЦФ (функции Лагранжа). Как только значение ЦФ перестает
29

увеличиваться и начинает уменьшаться (или наоборот) следует вернуться на один шаг назад, уменьшить шаг дискретизации по и продолжить варьирование. Так можно обеспечит любую необходимую точность вычислений.
▲
4. Методы и алгоритмы экспертного оценивания
Экспертом называют лицо компетентное в данной области знаний и способное делать необходимые оценки объектов на основании текущей или ранее полученной информации.
Эксперт – это своеобразный измерительный прибор, позволяющий измерить то, что нельзя оценить иным способом.
Основные этапы экспертизы:
1.формирование множества объектов;
2.формирование экспертной комиссии;
3.выбор процедуры экспертного оценивания и опрос;
4.обработка результатов экспертного оценивания;
5.анализ результатов экспертизы и принятия решения.
Важными этапами экспертизы являются проведение опроса экспертов и дальнейшая обработка результатов. Их и рассмотрим более подробно.
Различают следующие методы опроса:
1.Индивидуальный и групповой. При индивидуальном опросе ответы эксперта остаются неизвестными остальным участникам экспертизы, при групповом - оценки каждого эксперта доводятся до сведения остальных.
2.Очный (интервьюирование) и заочный (анкетирование). При заочном - ответы даются экспертами в письменном виде. Анкетирование может проводиться с обратной связью и без нее.
3.Открытый, ответ на который даѐтся в произвольной форме. Закрытые вопросы обычно сопровождаются набором вариантов ответов.
4.Прямой и косвенный. В прямом эксперты знают цель проведения экспертизы, а в косвенном нет.
5.С заданным и с неопределѐнным множеством объектов.
6.Простые и сложные. Сложные обычно раскладываются на ряд простых процедур.
7.Качественные и количественные.
4.1. Шкалы измерений
На практике не все характеристики объектов могут быть измерены в абсолютных единицах (метрах, рублях, тоннах и т.п.). Это связано с типом шкалы, по которой эксперт может оценивать объекты. Грубые оценки обычно формируются по качественным шкалам, а более тонкие - по количественным.
Измерения |
Шкалы |
Допустимые |
|
преобразования |
|||
|
|
||
Качественные |
Номинальная |
Н (x) - однозначные |
|
|
Порядка |
П (x) - монотонные |
|
Количественные |
Интервалов |
И (x) x , 0 |
|
|
Отношений |
О (x) x, 0 |
|
|
|
|
|
|
Разностей |
Р (x) x |
|
|
Абсолютная |
А (x) x |
30
