
- •1. Призма и пирамида
- •2. Построение правильных пирамид и призм
- •3. Сечение прямоугольной трубы
- •4. Построение сечения пирамиды
- •5. Пересечение пирамиды линией и призмой
- •6. Последовательность построения 2-х многогранников
- •7. Построение сечения цилиндра
- •8. Построение развертки цилиндра
- •9. Возможные сечения конуса
- •10. Построение сечения конуса и его развертки
- •11. Построение сечения шара
- •12. Построение сечений тора
8. Построение развертки цилиндра

Рис. 8
Построение развертки (рис.8). Полная развертка состоит из четырех частей: развертки боковой поверхности, ограниченной пятью отрезками прямой линии и кривой A0l0B0 - синусоидой; натурального вида фигуры сечения; круга основания цилиндра; сегмента, полученного на верхнем основании.
Полная развертка боковой поверхности цилиндра - прямоугольник с высотой, равной цилиндру, и длиной L = πd, где d - диаметр цилиндра. Для построения на развертке точек линии среза развертку основания цилиндра делят на такое же число частей, как и при построении проекций линии среза. Проводят через точки деления образующие и отмечают на них высоту до точек эллипса среза - точки 10 20 и 120, 30 и 110, 40 и 100, 50 и 90, 60 и 80, 7.Соединяют построенные точки плавной кривой - синусоидой. Натуральный вид фигуры среза цилиндра плоскостью выполнен ранее(1IV2IV3IV…12IV) и его по координатам строят на развертке.
Построим на чертеже цилиндра проекции точки, указанной на разверстке точкой М0. Для этого отметим хорду l2 между образующей, на которой расположена точка М0, и образующей точки 4. По хорде l2 строим горизонтальную проекцию М' и по известной высоте ее расположения найдем ее фронтальную проекцию М".
9. Возможные сечения конуса

Рис. 9
10. Построение сечения конуса и его развертки
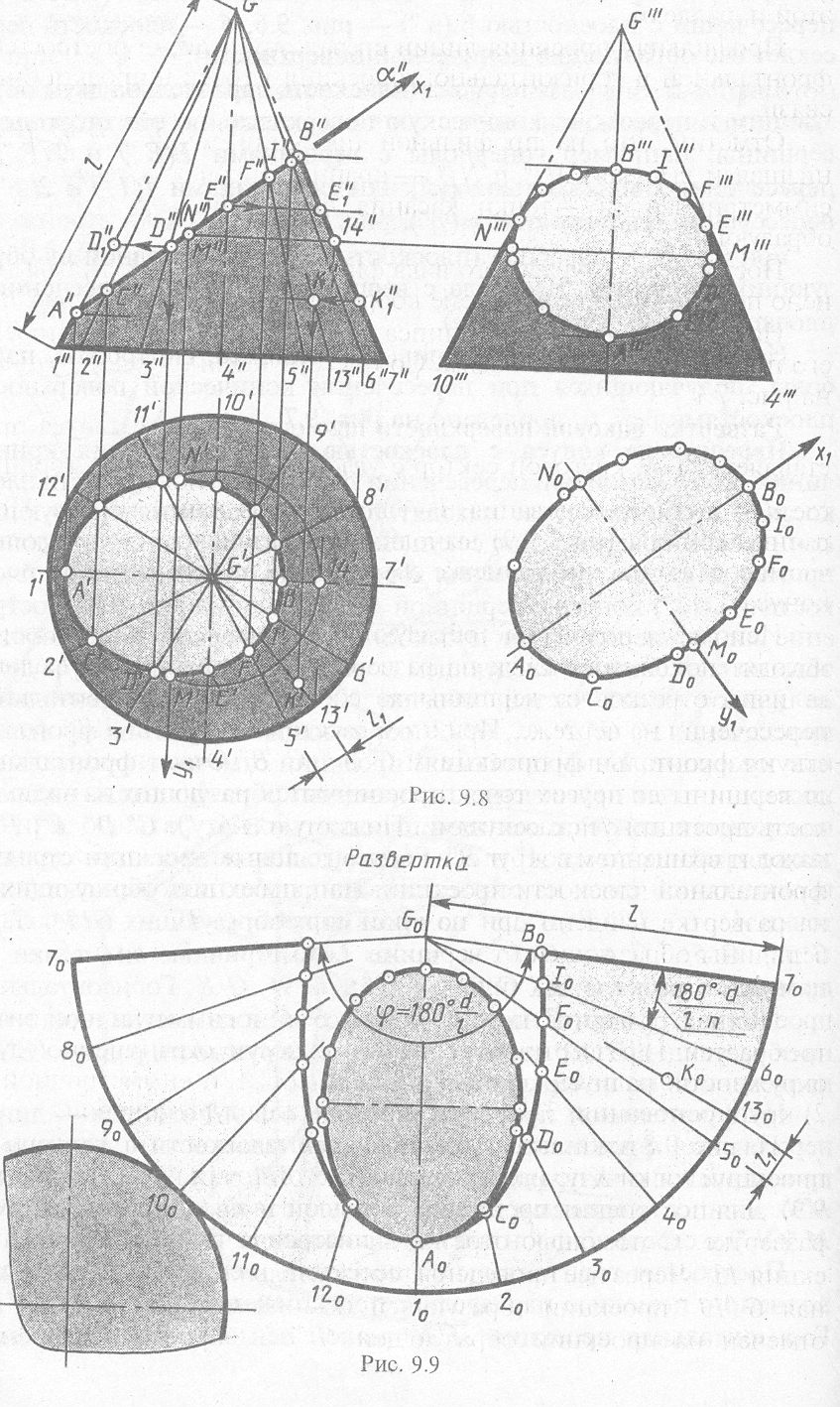
Рис. 10
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор с углом φ = d/l × 180 ° при вершине, где d - диаметр основания, l - длина образующей конуса. Построение сектора (рис. 10 внизу) выполняют с разбивкой его на равные части соответственно разметке образующих на чертеже (см. рис. 10 конуса).
Используя положение образующих на чертеже и на развертке находят положение точек на развертке при помощи натуральных величин отрезков от вершины до соответствующих точек линии пересечения на чертеже. При этом расстояния G0A0 и G0B0 соответствуют фронтальным проекциям G"А " С"В". Отрезки образующих от вершины до других точек проецируются на фронтальную плоскость проекций с искажениями. Поэтому их натуральную величину находят вращением вокруг оси конуса до положения, параллельного фронтальной плоскости проекций. Например, положение точки D0 на развертке найдено при помощи отрезка G "D1" - натуральной величины образующей от вершины G до точки D точки E0, - при помощи отрезка G"Е1" (или G'"E'").
Полная развертка поверхности усеченного конуса состоит из трех частей: 1) развертки боковой поверхности, ограниченной дугой окружности радиуса l, кривой B0I0F0E0D0C0A0 и симметричной ей; круга основания; 3) натурального вида фигуры сечения.
На рис. 10 (вверху) показано построение фронтальной и горизонтальной проекций точки К по изображению К0 этой точки на развертке (рис.10). Для построения проведена образующая G0130 через точку К0 на развертке. С помощью отрезка l1 построена горизонтальная проекция 13'. Через нее проведены горизонтальная G' 13' и фронтальная G"13 " проекции образующей G - 13. Отрезок G0K0 = G"K1" на проекции образующей G "7 ". Обратным вращением построена фронтальная проекция К" точки К на фронтальной проекции образующей G"13".Горизонтальная проекция К' построена с помощью линии связи.
