3 группа / Процессы переработки пластмасс / Контрольные работы (1 семестр) - Шпаргалки - Шерышев - 2004 / ММ_проц_переработки 2-я контр

Валки вращ. С одинак. Скор. Допущения:

1. Ж-ть несжимаема и смачивает пов-ть валков.

2. Проц. Изотермический

3. Пренебрегаем массовыми силами.

4. Ж-ть подчин з-ну вязкости Ньютона.

5. Валки не обладают фрикцией.

1. Опред. Пройзв. Вальцев в корд с т. Х

- произв. вынужд потока.

- произв. обр. потока

2. Определим производительность при корд Хк

- обр. поток равен 0

Учитывая неразрывность потока в межвалк.зазоре

Приравниваем, и выражаем dp/dx

Заменим Х на безразм. Независ. Корд. Для

этого рассмотрим треуг. ОАВ

; Пусть -

;

- h_к – по аналогии

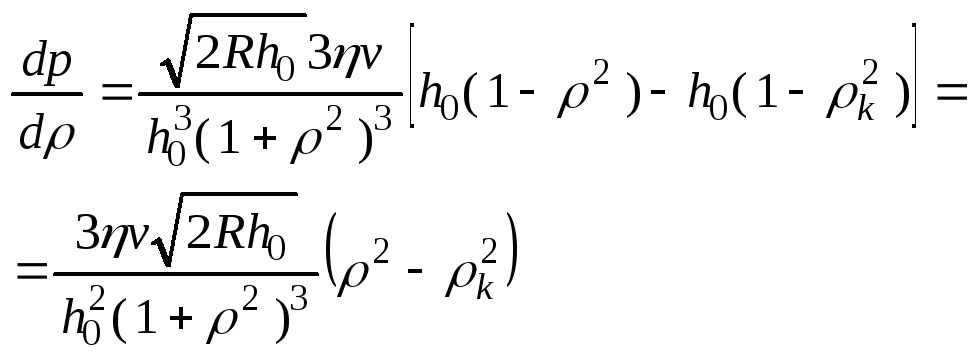
Проинтегрировав получим:

Пост интегр с пред из гранич усл при , Р=0

Обычно

Распорное усилие и треб мощн находим для Рмах.

; F- распорное усилие

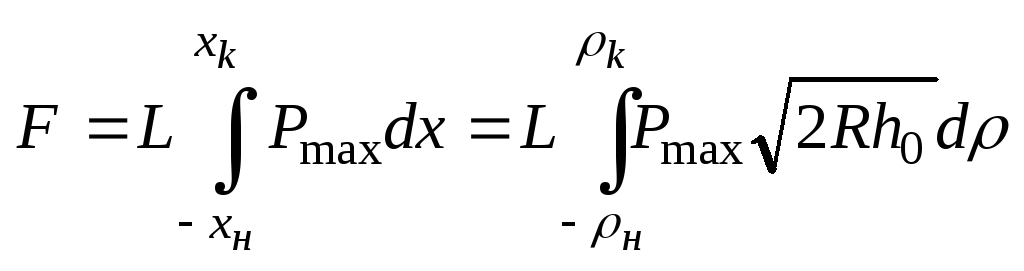
и находят из графиков

; Для опред мощности

необходимо опр крут М на валке

;

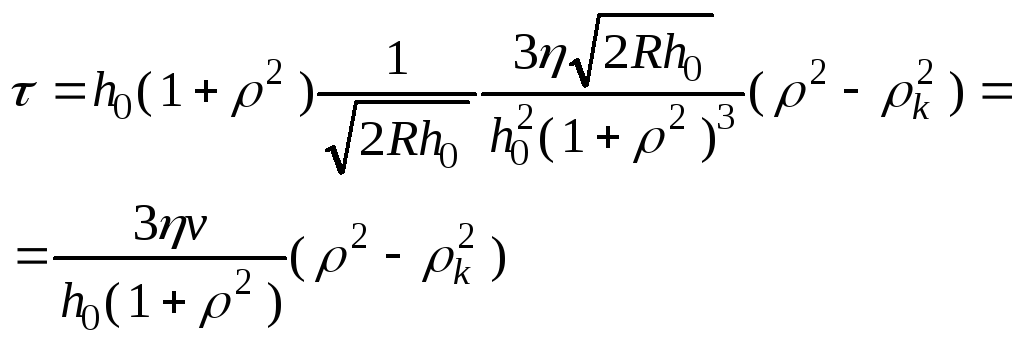
Проинтегрируем:

Мощность, затрачиваемая на вращение валков

; - угловая скорость;

Расчёт валковых машин для неньют ж-тей

Для ньют. ж-тей

Для неньют.ж-тей ;

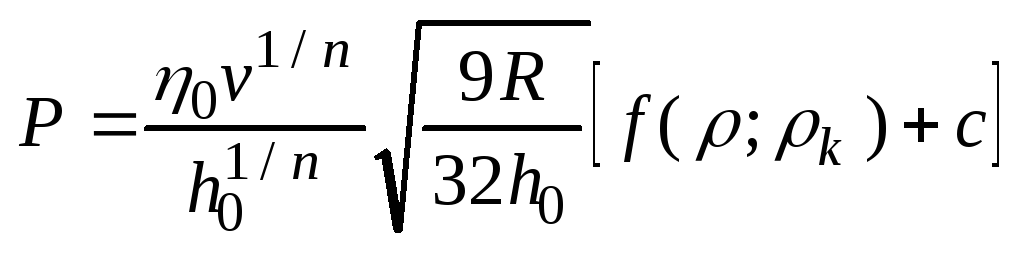
- эффект. Вязкость

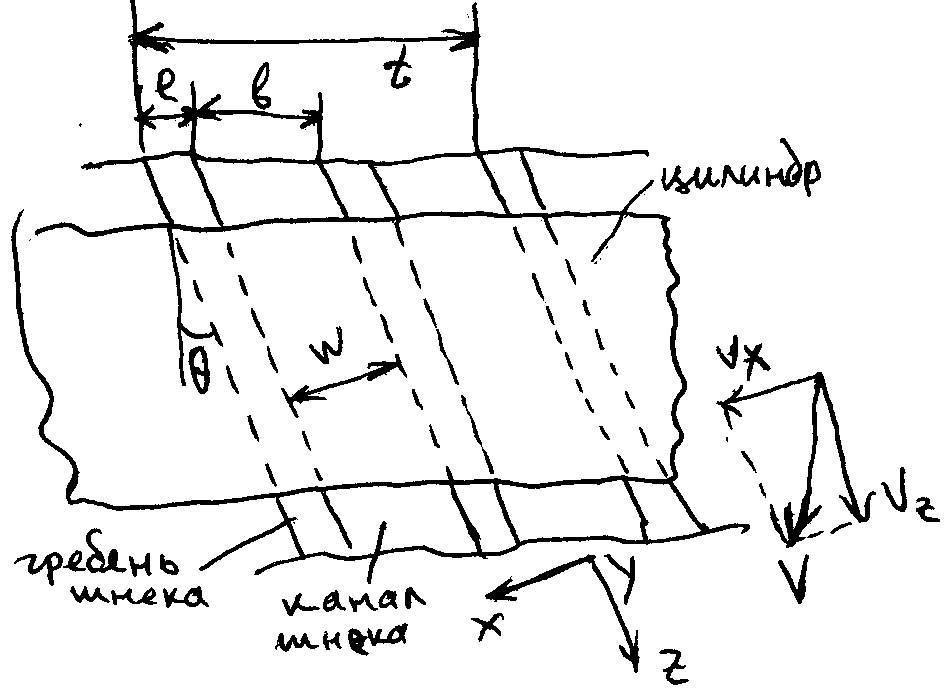
Одночерв. Экструд. Расчёт зоны питания

Допущение: в пробке отс. деформ.

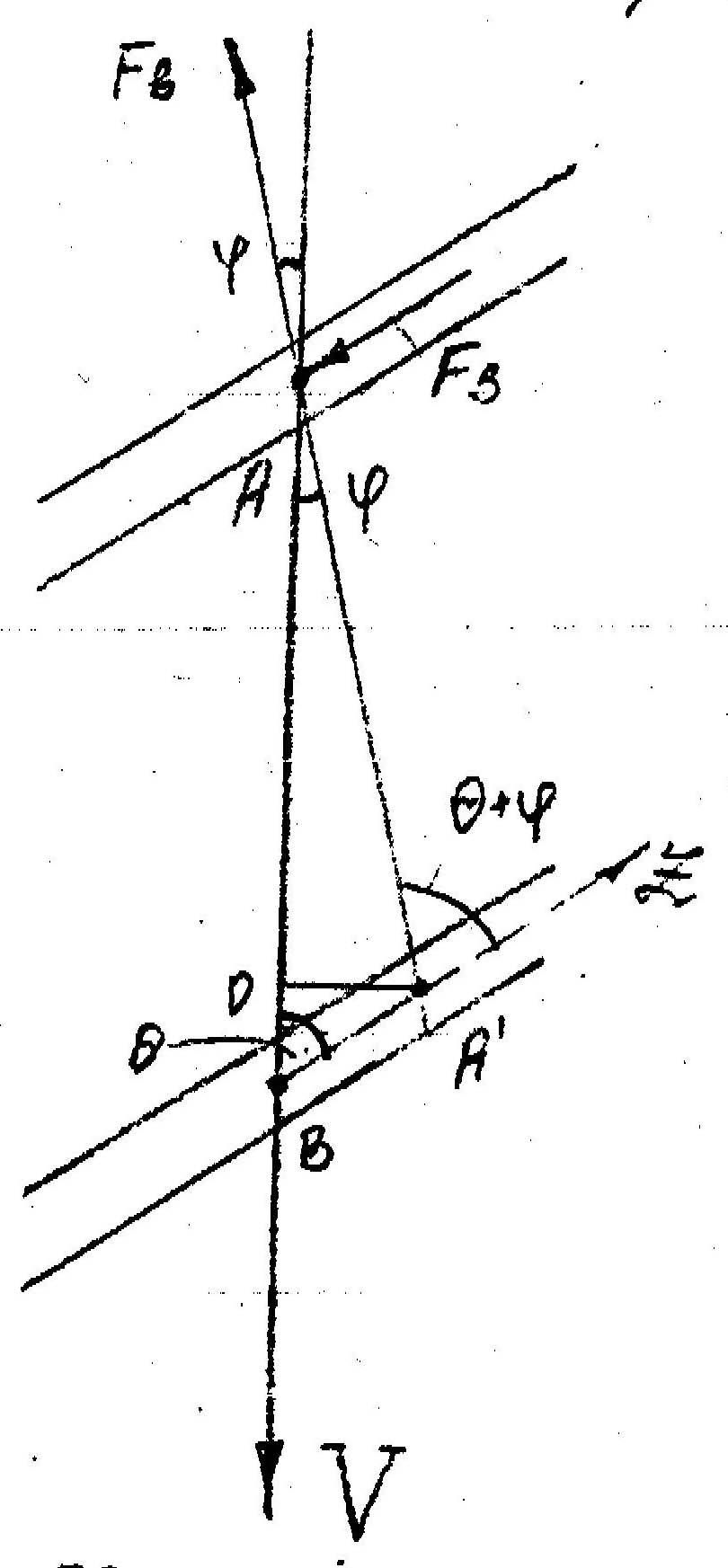- Угол наклона

винт. линии

V- скор. Движ шнека

Относит. Цил-ра

Геом. Стор. Задачи

Рассм. 2 треуг-ка

АОА’ и ОВА’

Из ОВА’

или

из АОА’

или

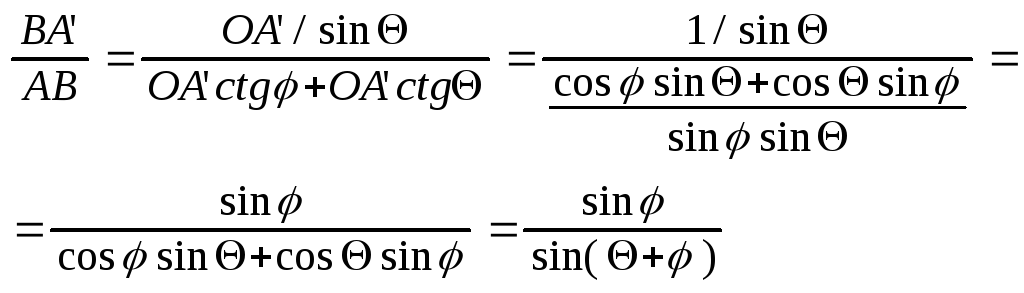
Физическая сторона задачи

Определение скорости перемещ ч-цы

Скор. Переем. Ч-цы вдоль выступа шнека

;

V – опред. напрямую из числа об. Шнека

F_b – сила трения о цилиндр

F_S – сила трения м-ла о шнэк

Введём обозначение:

Рассмотрим 3 крайних случая:

1. Пусть , тогда

При мат-л перестаёт продвиг вперед

и вращается вместе со шнеком.

2.Пусть , тогда

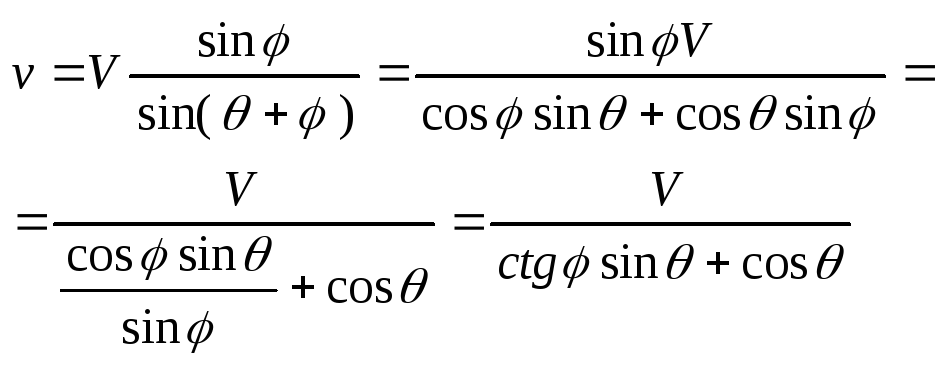
разделим обе части на

3. Пусть

----------------------------------------------------

Предп.,что пробка при движ. Оказ на все

Соприкос с ней стенки одинак давление

Тогда:

- площ сопр пробки с шнеком и цил.

- коэф тр пробки о шнэк и о цил.

; L- длина зоны загрузки.

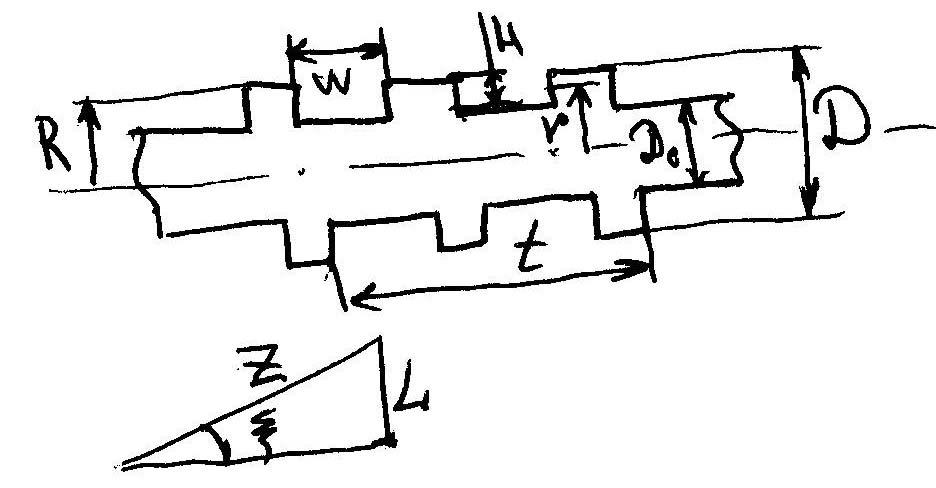
t – шаг при двухзаходном шнеке

Н – высота гребня.

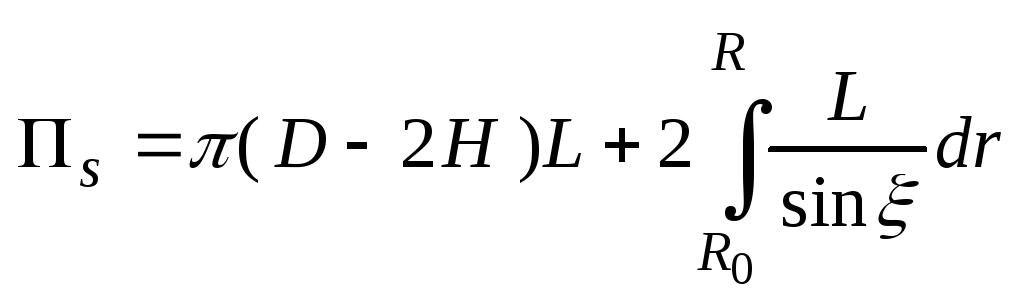
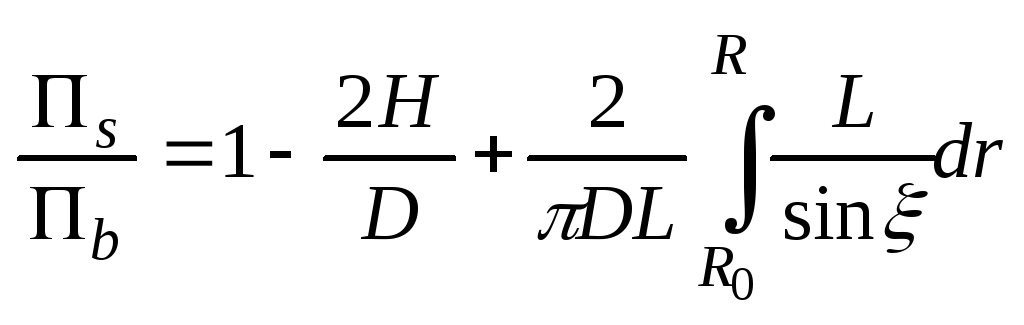
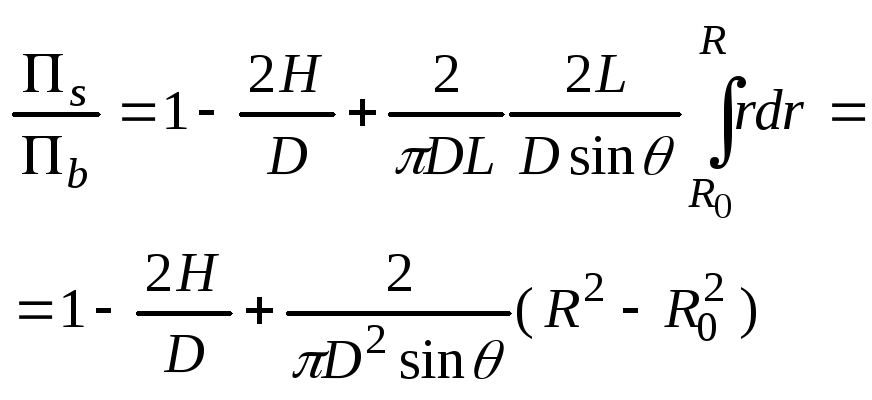
Расчёт одношн машин по зоне дозиров

При расчёте одношн. Машин по зоне дозиров

Делают следующие предположения:

1. Винт канал, образ. Нарезкой шнека и внутр

стенк цил, рассм разверн в плоск (плоск задача)

2. Счит что шнек неподв а цил движется со

скор V в направл перпендик оси шнека.

3. Пренебрег. Массовыми силами.

4. Счит. что р-в полностью заполн каналы

шнека и прилипает к нему

5. Ж-ть несжим и имеет одну и ту же t по

всей длине зоны дозиров (изотермич проц).

6. Рассм канал прямоуг формы с пост размер

по длине, т.е. поперечное сеч канала не явл

ф-ией текущей координаты

7. Ширина винт канала w много > его глубины

H, w>>H

8. учит только поперечн и продольн комп

скор движ р-ва. Предпол, что вертик сост-щая

скор не оказ существ влияния на проц экстр.

Выведем Ур-е кол-ва движения, прим-но к рассм

задаче. Выделем элем объём р-ва наход в канале

шнека.

Сост. ур-ие равновес этой ч-цы.

;

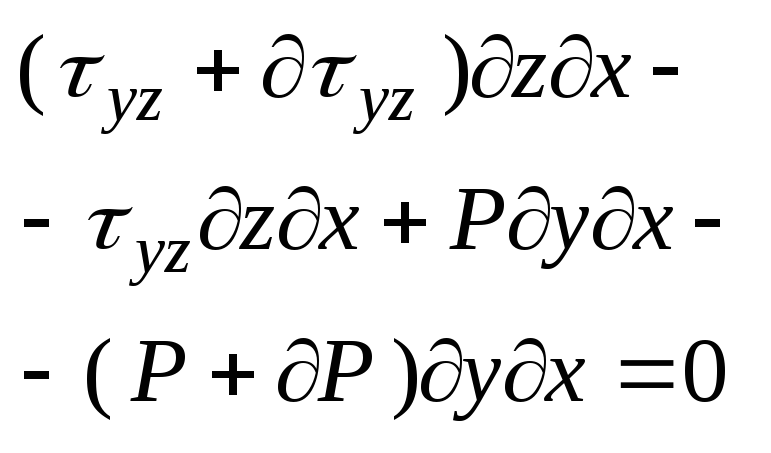
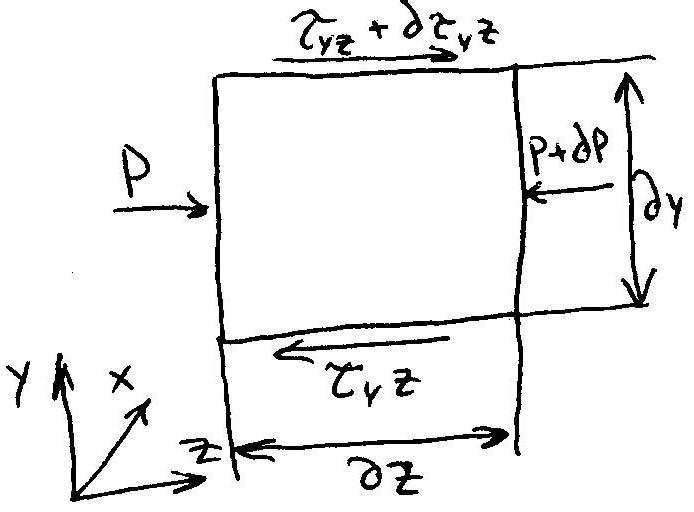
З-н вязкости ньютона:

; ;

(1)

По аналогии: (2)

Воспользуемся уравнением (1)

Дважды проинтегр это Ур-ие, опр скор

Пост интегр-я найдём из гранич условий:

При у=0; (3)

При у=Н; (4)

Из Ур-я (3) следует, что С2=0

Из Ур-я (4) получ:

;

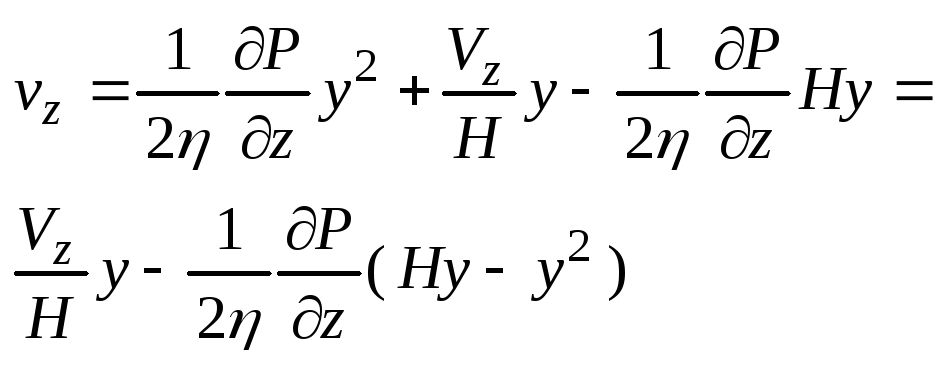
1- скорость вынужденного потока

2-скорость обратного потока

Определим составл скор-ти в направл оси Х

Пост интегр-я найдём из гранич условий:

При у=0; (3)

При у=Н; (4)

Из Ур-я (3) следует, что С2=0

Из Ур-я (4) получ:

;

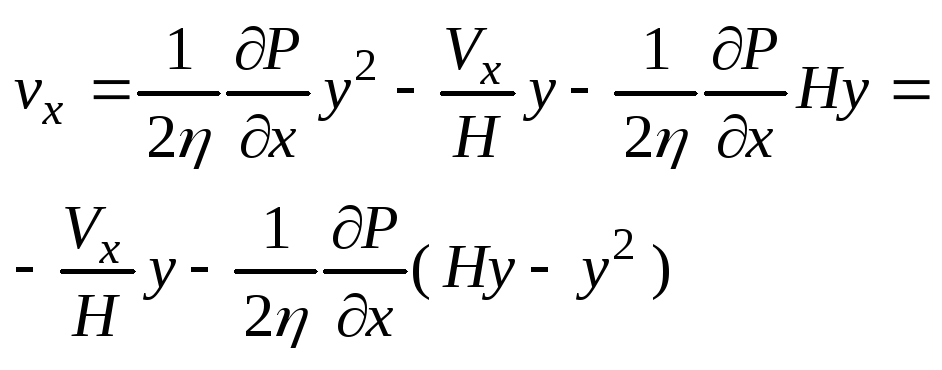
1-ый член Ур-я опис скор вынужд потока ж-ти,

обусл наличием комп-ты скорости Vx

2-ой член – это скор обр потока под действием

перепада давления

Появл комп скор объясн-ся нал-ем поперечн

цирк-ии ж-ти в винт канале шнека. Эта цирк-я

происх благод толк возд бок стенок винт кан.

Если пренебр утечками м-ла через рад зазор ,

то произв-ть поперечн потока равна 0.

; ;

Опред из этого

Подставим в уравнение для опр-я

Опред пр-ть потока вдоль оси Z, т.к. именно эта

Пр-ть и есть пр-ть экструдера по зоне дозиров

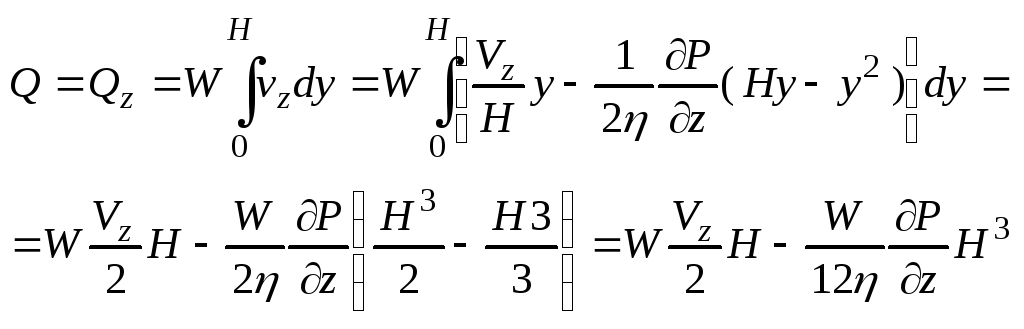
Перейдём от этого вида ур-ия к ур-ю, сод только

пар-ры, входящ-е в технич х-ку одношн экструдера

; ;

- сопротивл головки; L – длина зоны дозиров.

Как видно из расчётной схемы:

; ;

D – диаметр шнека;

t – величина шага; i – число заходов

; С учётом потока утечки это

Ур-ие принимает вид:

Опред соотн между общей Q и Q вынужд потока

; ;

- вынужд пот. - Противоток.

При полностью закрытом проходе в формующей

Головке коэф=1, отн-е, т.к. Q=0

Расч мощн привода одношнек. Экстр по зоне доз.

Рассмотр в движ вдоль оси канала шнека плоск

пластинку площ ds, на кот действ сила dF,

способств перемещ пластины со скор V. Тогда

мощность, затрач на перемещ. пластины:

; Разложим вел-ны скор и силы по

осям X и Z:

; ;

;

При принятой нами схеме движ-я наиб напряж

будут возник при у=Н. А при опр мощности,

затрачиваемой в проц экструдирования нас

интерес max напряж и усилия.

; Подст Н вместо у

;

; При у=Н

;

Сила действ в напр Х им знак «-», т.к. она напр

навстр оси Х, но при опред мощн необх на продв

мат-ла направление силы не имеет значения

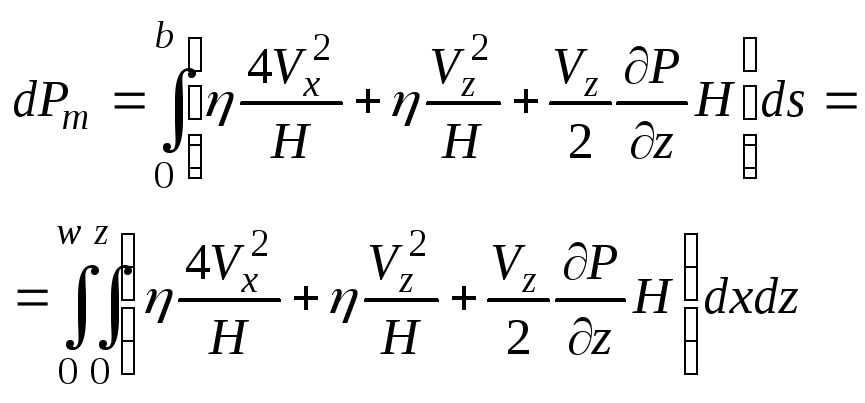
Мы опр мощн затрач лишь на передвижение м-ла

вдоль канала шнека.

В рад зазоре происх пост трение р-ва о нарезку

шнека и материальный цилиндр.

Определим эти затраты мощности.

; ;

; ;

;

Однако пр выводе этих Ур-ний не учит мощн

Затрачив в зоне питания и в зоне пластикации,

А также мощн теряемая в приводе экструз

машины. На практ уд энерг экструз большинства

П лежит в диапазоне 0,13(наим вязк)..0.234(наиб

вязк) кВт/кг.

Если пренебр теплом, кот подвод от внеш нагрев,

То кажд кВт мошн привода обеспеч производит

от 3,7(наим вязк) до 7,4(наиб вязк) кг/ч

Производит дозир зоны шнека с переем шагом

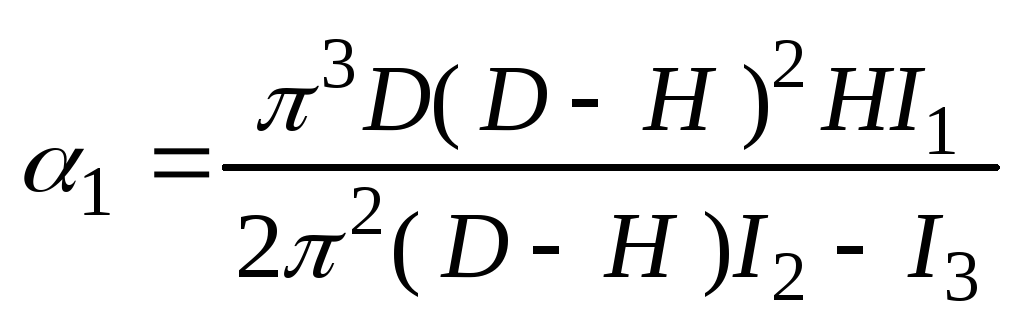
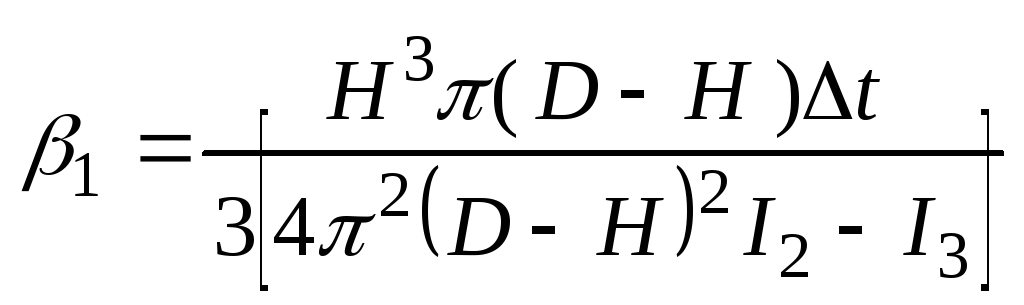
- шаг в начале зоны; - шаг в конце зоны

m – число шагов в зоне дозирования

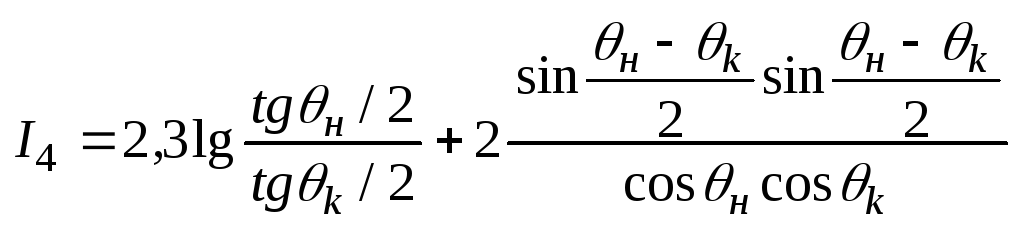
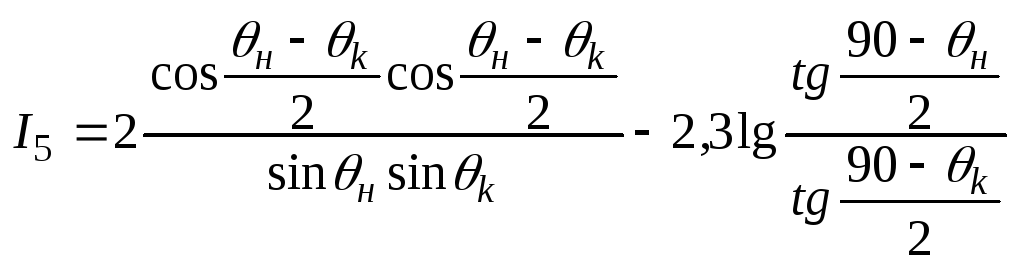
Производит дозир зоны шнека с перем глуб винк канн

;

t – пост шаг; I – число заходов; е – ширина гребня

Hn – глубина нарезки перв витка зоны дозиров

Hk – глубина нарезки последнего витка

d1 - диаметр серд шнека в начале зоны дозирования

d2 – диаметр серд шнека в конце зоны дозирования

;

L – длина зоны дозирования.

Опред производит зоны дозир с учётом сопр головки

Рассм головку как некий канал, кот мы схематично

можем разбить на неск послед-ных каналов, кажд

из кот имеет дост-но прост геом форму. В этом

случае произ-ть истечения р-ва через этот канал

будет прямо пропорц перепаду давл-я, обеспеч перем

ж-ти черезэтот канал и обратно проп ж-ти.

; ;

к – коэф геометрии головки (геом. коэф)

;

;

Т.о., зная к, можно посч произ-ть любого экструд.

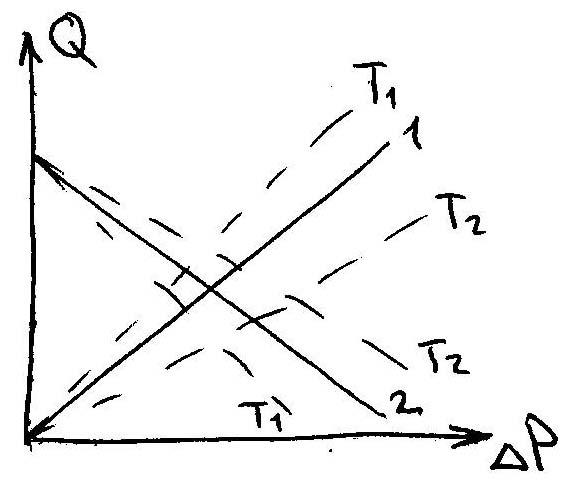
1 – х-ка головки

2 – х-ка экструдера

Т1>Т2

Принцип расчёта экструзионных головок.

Допущения:

1. Геом коэф к явл вел-ной пост., т.е. исключ

временные или местные изм-ия t.

2. Течение р-ва стационарное и неламинарное.

3. Массовыми силами принебрегаем.

4. М-л прилипает к стенкам канала и ц-ра.

Исп ур-е равновес м/у дав-ем выдавл и напр сдв .

Рассм. расч кан голов на прим. канала кругл. Сечен.

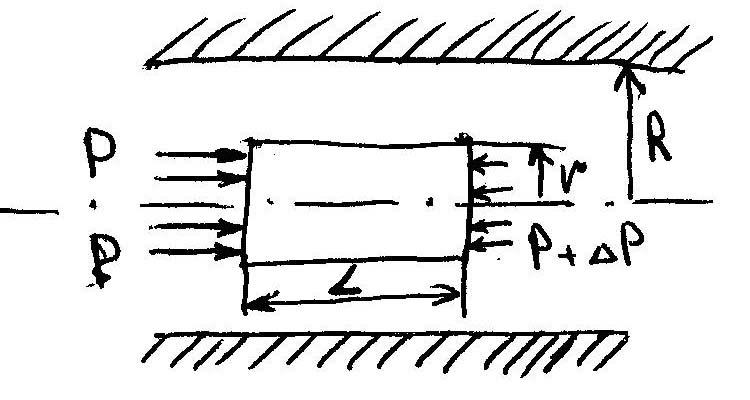
По границ выдел Эл-та действ касат напр., т.к. ж-ть

облад опред вязкостью.

Силы, заставл Эл-т ж-ти продвиг вперёд:

Силы препятств. собств движ эл-та:

; ;

Из з-на вязкости Ньютона следует:

;

;