
3 группа / Процессы переработки пластмасс / Контрольные работы (1 семестр) - Шпаргалки - Шерышев - 2004 / ММ_проц_переработки 1-я контр
.docЦель курса: Знакомство с аналитическим описанием распространённых процессов переработки пластмасс.
Каждый из процессов разделяется на элементарные стадии:
Подготовительные стадии:
1. Перемещение сыпучих или несыпучих тв. материалов
2. Нагрев(плавление)
3. Перекачивание и создание давления.
4. Смешение
5. Дегазация и разделение продуктов.
Формование изделий. Виды:
1. Экструзионное
2. Розлив с давлением или без давления.
3. Вторичное формование
-) раздувное
-) из листов и плёнок
4. Каландрование
5. Оболочковое (ротац и центробежное)
Механическая обработка.
Понятие ММ процессов переработки.
ММ – имитация реального перераб. оборудования и процессов формования с помощью математических формул.
Точность описания св-в сырья, технич и геом. параметров рабоч. органов перераб. оборудования зависит от:
наличия или отсутствия достаточн базы данных, достоверности используемых законов и предположений.
В итоге ММ всегда является лишь приблизительной аппроксимацией реально протекающего процесса.
ММ могут содержать:
1. только системы алгебр. уравнений.
2. только системы дифф. уравнений.
3. только системы интегральных уравнений.
4. все возможные комбинац. различных уравнений.
5. численные методы решения в виде соотв программ для ЭВМ.
Признаки классификации процессов переработки:
1. В соотв. с природой процесса:
а) детерминированные. Каждая переменная или параметр принимает некоторое опред. значение (или ряд значений) в зависимости от заданных условий. (больш. процессов).
б) стахостические. Изменение переменных или параметров неопределённо. Можно определить лишь их наиболее вероятное значение.
2. В соотв с математической основой на которой строится модель:
а) аналитические модели, основой для которой являются фундаментальные законы химии, физики, механики сплошн сред и т.д.
б) эмпирические модели, основой для которых являются экспериментальные данные.
3. В соотв. с характером описываемого процесса.
а) Стацион. процессы. (экструзия каландрование)
б) нестационарные процессы.
4. В соотв. с характером изменения параметров от заданных условий.
а) линейные
б) нелинейные.
Смешение. Сыпучие материалы и высоковязкие жидкости.
Общие понятия и определения.
В состав смеси могут входить 2 или более компонентов.
Смешение- изменение первоначального распределения компонентов в смешиваемом объёме.
В курсе рассмотр. 2-ух комп. смешения. При переходе к многокомпонентным смесям мы считаем, что каждый последующий компонент смешивается с ранее приготовленной смесью.
Компонент смеси, конц-я которого в данном объеме наибольшая называется основным, остальные – ключевыми.
Виды смешения:
а) Обычное(простое) – процесс, в результате которого увеличивается случайность простр. распределения вводимого в-ва в основном компоненте. Простое смешение осуществляется без изменения размеров частиц компонентов.
б) Диспергирующее – происходит как уменьшение ч-ц вводимого в-ва, так и увеличение статического беспорядка в их распределении.
Основные мех-мы смешения:
а) диффузионное смешение
б) турбулентное (в поток основного в-ва, движ в турбулентном режиме, добавляют ключевой компонент)
в) Деформационный (к основному компоненту прикладывают большие сдвиговые деформации и под действием этих деформаций ключевой компонент «втирается» в основной компонент)
г) Гидродинамический (для смешения используют направленное движение потоков компонентов)
Критерии качества смешения.
Идеальная смесь – смесь, для которой присутствие любого компонента в любой точке объёма остаётся постоянным.
В микрообъёмах перемешиваемых компонентов возможно бесчисленное разнообразие взаимного соотношения частиц комп. Таким образом, соотношение компонентов в определённой точке объёма есть величина случайная. Для двух компонентных смесей случайным является распределение ключевого комп-та. Эта случайная величина охарактеризована если известно:
а) вероятность того или иного соотношения частиц в смеси.
б) материальное ожидание этого соотношения.
в)
Средне квадратичное отклонение![]() и
дисперсия
и
дисперсия
![]()
Смешение сыпучих компонентов
Пусть обшее число частиц в пробе – m.
Доля
частиц ключевого компонента во всём
объёме-![]()
Тогда вероятность того, что в отобранной пробе содержится b частиц ключевого компонента:
![]()
Математическое ожидание появления ключевого компонента в основном в общем виде:
![]()
![]() -
значение конкретных величин в каждой
пробе.
-
значение конкретных величин в каждой
пробе.
![]() -
вероятность
-
вероятность
![]()
![]() -
средн конц ч-ц ключевого комп. в основном
-
средн конц ч-ц ключевого комп. в основном
![]() ;
N
– число
проб.
;
N
– число
проб.
![]() -
конкретное значение концентрации
-
конкретное значение концентрации
![]() ;
;
![]() -
общее число частиц в пробе.
-
общее число частиц в пробе.
Квадратичное отклонение:
![]()
![]() -
критерий качества смешения
-
критерий качества смешения
![]() ;
; ![]()
0 – ключевой и основной компоненты не смешаны.
1 – идеальное смешение
Критерии качества для вязкотекучих компонентов
Условно считаем чёрный компонент – ключевым, белый – основным.
Смешение высоковязких жидкостей – следствие деформаций сдвига, в результате которых происходит увеличение пов-ти раздела комп. и преобр-ие их распределения в случайное неупорядоченное.
При
перемещении за счёт сдвиговых деформаций
площадь пов-ти раздела
![]() между
компонентами смеси увеличивается и
может достигнуть предельной величины
между
компонентами смеси увеличивается и
может достигнуть предельной величины
![]() в
полностью смешанном материале:
в
полностью смешанном материале:
![]()
a – эмпирическая константа, характеризующая свойства материала и особенности смесительного оборудования.
t – время смешения.
В результате смешения возм. 3 случая.
1) в пробе только белый компонент (3)
2) в пробе только чёрный компонент (2)
3) в пробе оба компонента (1)
Критерием качества смешения выбрана толщина полос.
Идеальное смешение – смешение при котором толщина полос равна нулю.
При ламинарном движении, характерном для высоковязких жидкостей, качество смешения значительно зависит от первоначального распределения основного и ключевого компонента.
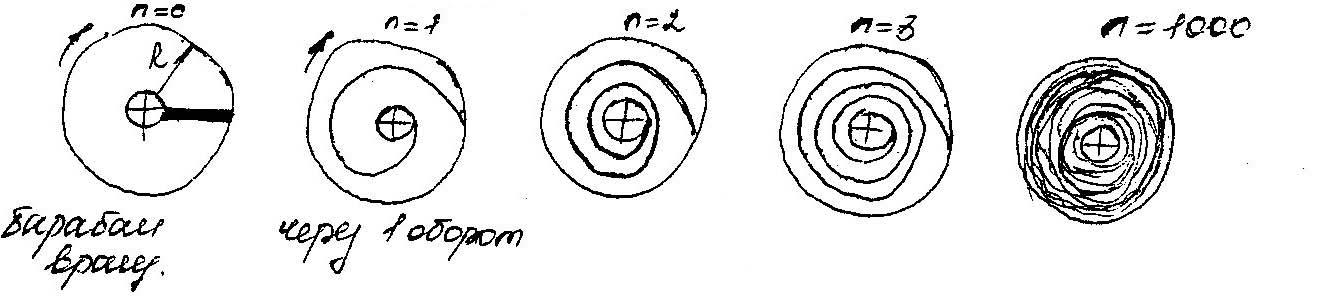
n – число оборотов
Толщина
полосы r
равна:
![]()

Зависимость между толщиной полос, объёмом смешиваемого материала и площадью поверхности раздела компонентов.
N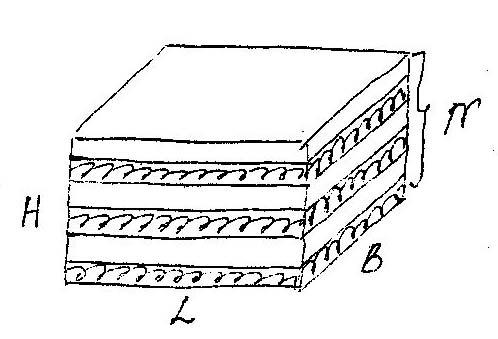 – общ число полос
– общ число полос
Н – высота
L – длина
В – ширина
![]() -
площадь поверхности раздела одной
полосы
-
площадь поверхности раздела одной
полосы
![]()
![]()
![]() Для всех полос:
Для всех полос:
![]()
Объём:
![]() ;
;
![]()
![]() ;
;
![]()
Толщина полосы прямо пропорционально объёму смешиваемого м-ла и обр проп. общ. площади раздела компонентов.
В
рабочих камерах смесителей при одноосной
деформации сдвига средний
![]() обратно
пропорц. величине сдвига:
обратно
пропорц. величине сдвига:
![]() ;
;
![]() -
величина сдвига.
-
величина сдвига.
Эта
зависимость справедлива для случая,
когда вязкости основного и ключевого
компонента равны. Если они не равны, то
![]() :
:
![]()
![]() -
вязкость ключ компонента;
-
вязкость ключ компонента;
![]() -
вязкость основного компонента.
-
вязкость основного компонента.
Докажем,
что
![]() является
вероятностной величиной и можно
достоверно характеризовать распределение
материала.
является
вероятностной величиной и можно
достоверно характеризовать распределение
материала.
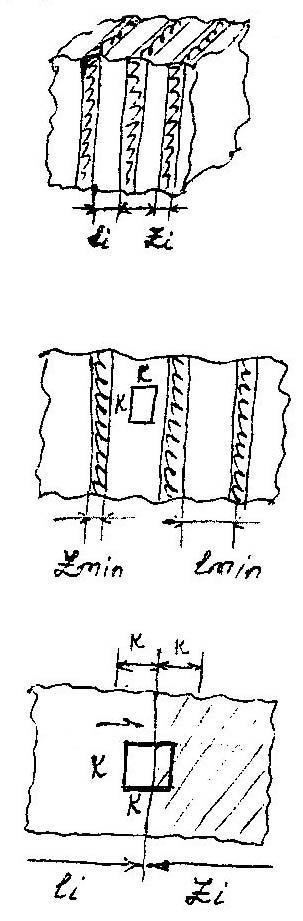
![]() -
толщина полосы основного компонента
-
толщина полосы основного компонента
![]() -
толщина полосы ключевого компонента
-
толщина полосы ключевого компонента
к – размер пробы
![]()
![]()
![]()
Пусть проба двигается слева направо.
Определить вероятность нахождения в пробе только чёрного материала.
Возможность
получения только чёрной пробы будет на
длине
![]()
N – общее число чёрных полос
Общий
путь движения
![]()
![]()
По
аналогии получение пробы с только белым
компонентом:
![]()
Определение получения вероятности проб с чёрными и белыми компонентами:
![]()
![]()
Вероятность
содержания только чёрного компонента
в пробах будет неравномерной, но
непрерывной и случайной величиной,
имеющей определённое значение
распределения
![]() .
Отметим 2 фиксированные величины:
.
Отметим 2 фиксированные величины:
![]() -
только бел и
-
только бел и
![]() -
только чёрный.
-
только чёрный.
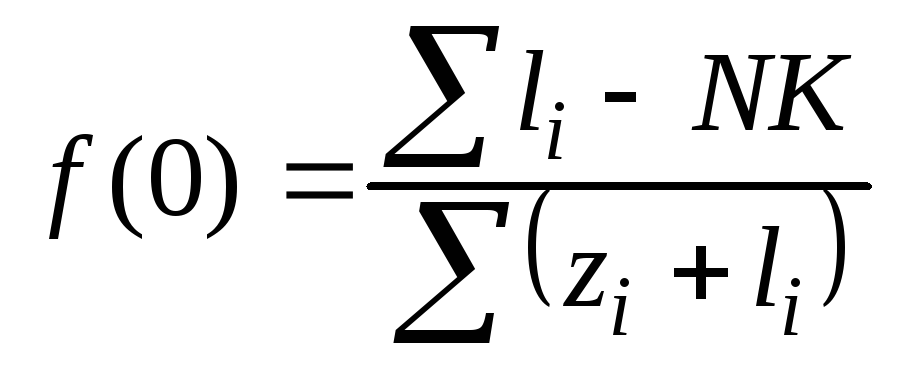 ;
; 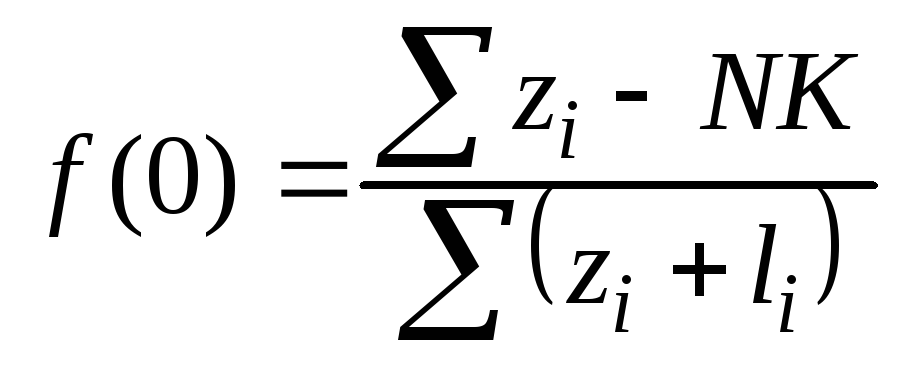
На отрезке от 0 до 1 распределение вероятности будет равномерным, а суммарное значение вероятности д.б. равно 1.
![]() ;
; ![]()
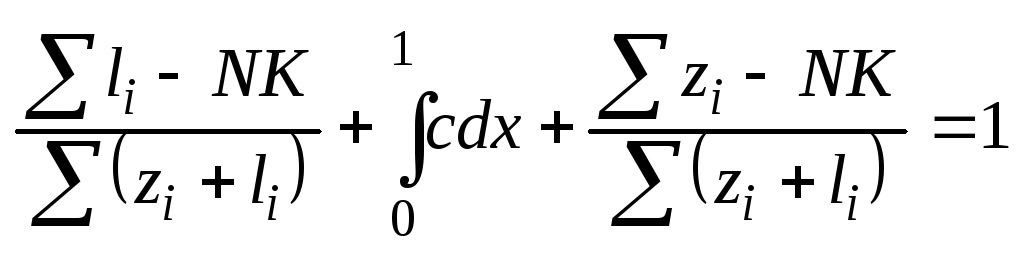
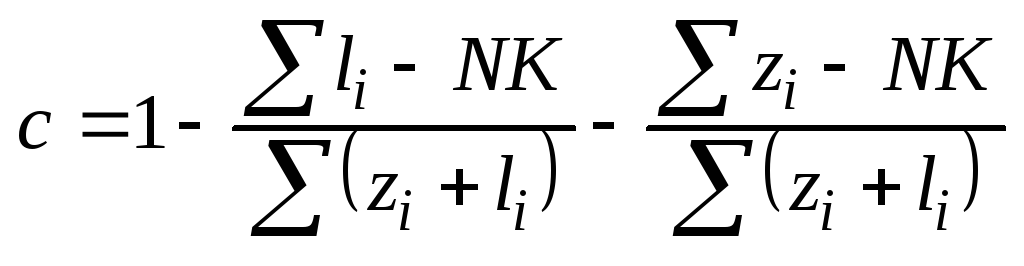
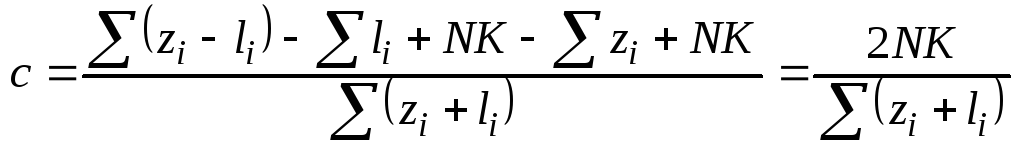
Математическое ожидание:
![]()
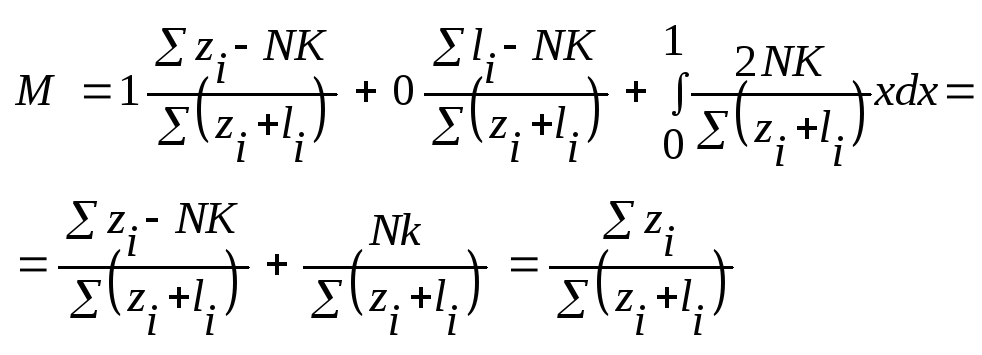
М появления только чёрного компонента равно его доле в смеси.
Дисперсия
ожидания
![]()
![]()
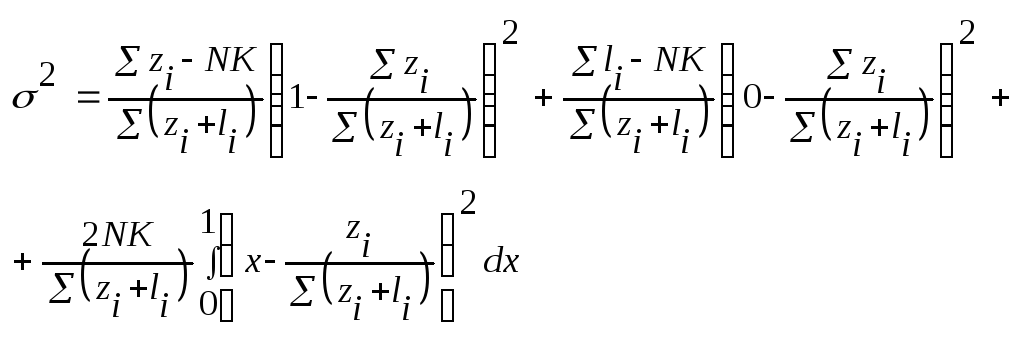
Проведя соотв. преобразования, полцчим:
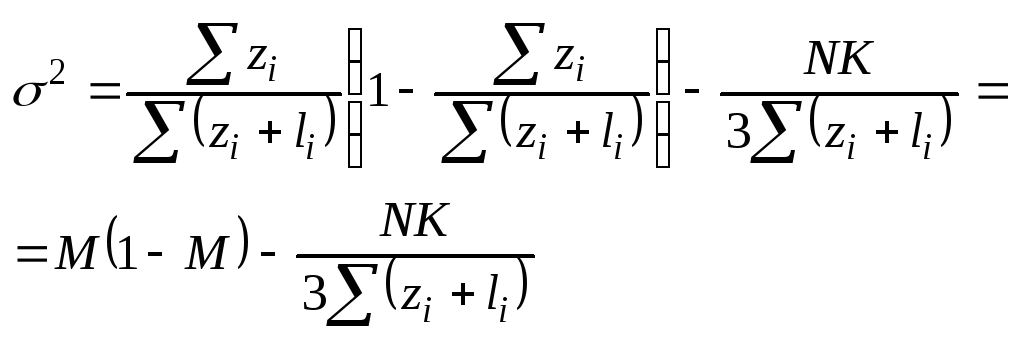
Толщину полос можно записать в следующем виде:
![]() ;
;
![]() ;
;
![]()
При
![]()
Тогда:
![]()
Полученная
зависимость доказывает, что средняя
толщина полос r
может служить столь же строгой
характеристикой, как и М и
![]()
Расчёт закрытого роторного смесителя
В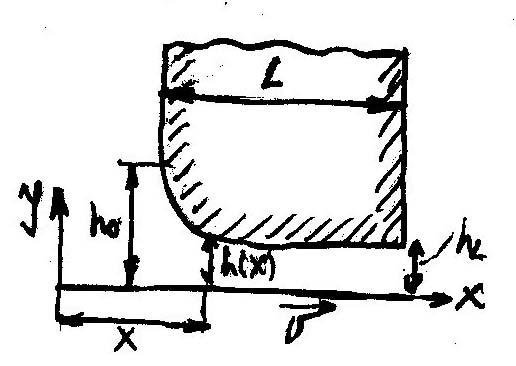 оспользуемся
принципом обращённого движения. Условно
счит., что ротор неподвижен, а стенка
камеры перемещается со скоростью v.
оспользуемся
принципом обращённого движения. Условно
счит., что ротор неподвижен, а стенка
камеры перемещается со скоростью v.
Воспользуемся уравнениями Гаскелло, которые будут выведены в разделе «Расчёт валковых машин»
![]() (1)
(1)
![]() (2)
(2)
Q – объёмный расход смеси, отнесённый к еденице длины ротора.
![]() -
коэф. вязкости
-
коэф. вязкости
Р – давление материала в зазоре
У- координата по высоте зазора
Допущение: Решаем задачу применительно к Ньютоновским жидкостям.
Из
Ур-я (1): ![]()
![]()
Давление м-ла на входе в зазор и на выходе из зазора равно нулю. Поэтому:
![]()
![]()
![]()
Введём
обозначения: Пусть
![]()
Тогда
получим:
![]() ;
; ![]()
Воспользуемся уравнением (2)
![]() Подставим
значение v:
Подставим
значение v:
![]()
Для
определения
затрат мощности необходимо
знать значение мах усилий, а следовательно
и мах напряжений. Мах напряжения в вязкой
ж-ти всегда возникают на её границе с
подвижными элементами оборудования. В
нашем случае с учётом допущения
![]() возникает
при
возникает
при
![]() .
.
![]()
Определяем мах усилие, препятствующее относительному вращению ротора:
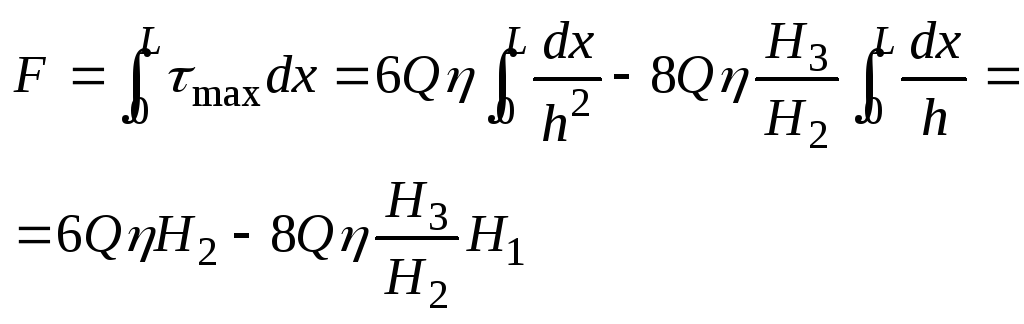
![]()
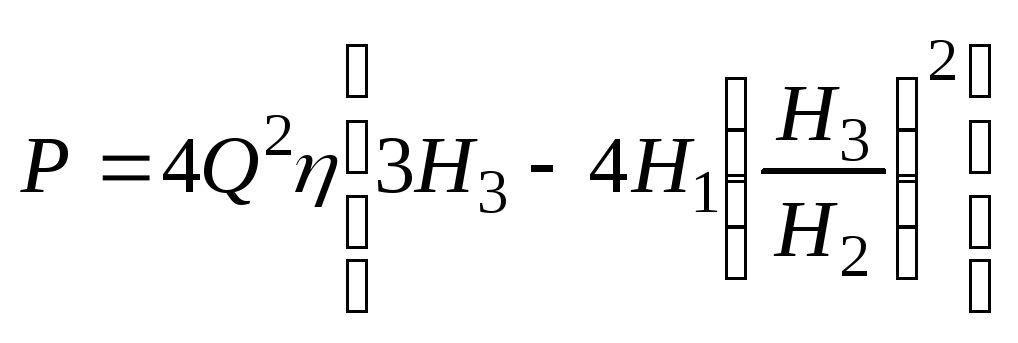 -
удельная мощность отнесённая к еденице
длины.
-
удельная мощность отнесённая к еденице
длины.
Мы
рассмотрели общий случай, когда величина
зазора описывается функцией
![]()
Рассм. случай, когда зазор является постоянной величиной (h=const) и не меняется от х.
Напряжение всегда направлено против скорости.
Упрощаем уравнение Гаскелло, учитывая только первые члены.
![]()
![]() ;
;
![]() (3)
(3)
В уравнении (3) знак «-» опущен, т.к. в отличие от скорости Q является скалярной величиной. Знак «-» теряет свой физический смысл.
Определение усилия:
![]()
![]()
Случай, когда зазор между ротором и стенкой камеры изм. по уравнению прямой линии.
Уравнение
:
![]() ;
; ![]()
Введём
обозначения:
![]()
![]() ;
; ![]() ;
; ![]()
![]()
Пусть
![]() ;
; ![]()
Пусть
![]() ;
; ![]()
![]() ;
; ![]()
![]()
Определённое удельное усилие:
![]()
![]()
![]() -
удельная мощность, отнесённая к единице
длины.
-
удельная мощность, отнесённая к единице
длины.
![]()
Коэф-т
![]() ,
,
![]()
![]()
Тепловой расчёт роторного смесителя закрытого типа.
1. На практике роторные смесители могут мнабжаться как системами охл-я, так и системами подогрева.
2. Тепловой расчёт всегда ведётся в режиме поверки.
3. При тепловом расчёте принимаются допущения о стационарности процесса смешения, т.е. мы считаем, что равные промежутки выделения или потребления одинакового кол-ва тепла.
4.
Для удобства разбиваем весь цикл смешения
на равные отрезки времени
![]()
![]()
Q – теплота
М – масса смеш.
с – уд. теплоёмкость
i – номер отрезка времени
![]()
к – коэф. теплоотдачи.
F – пов-ть теплоотдачи
Подставив в эти уравнения ср значения t воды и смеси и раскрыв t воды через её физич. параметры, получим след. уравнение:
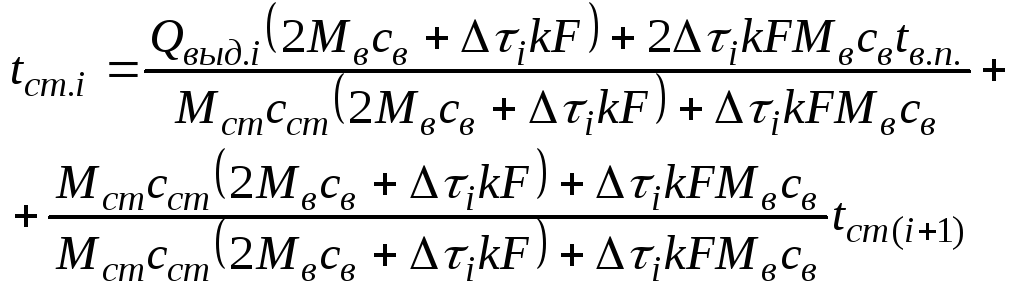
![]() -
масса охлажд. воды.
-
масса охлажд. воды.
![]() -
уд. теплоёмкость охл. воды.
-
уд. теплоёмкость охл. воды.
![]() -
t
воды начальная
-
t
воды начальная
Перепишем это уравнение в виде:
![]()
![]() через
интервал времени
через
интервал времени
![]() :
:
![]()
![]()
![]()
Расчёт лопастного смесителя.
Существует 2 метода расчёта смесителей:
1. В основу расчёта положен учёт наиболее значимых факторов, хар процесс и позволяющих, пользуясь законами механики, установить расчётную формулу для определения треб. мощности.
2. Связан с представлением о том, что сопротивление, возникающее на пути лопасти близко по своей природе сопротивлению тв. телу, движущемуся в вязкой жидкости.
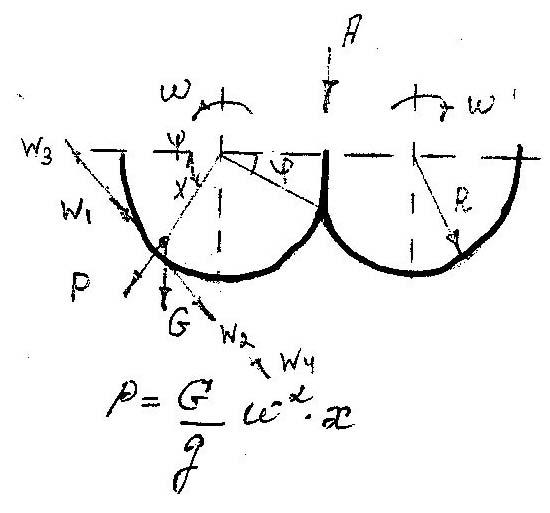
Р – избыточная сила; G – сила веса.
Рассмотрим те силы, которые мешают повороту лопасти.
w1 – сила трения лопасти о корпус.
![]()
f – коэф. трения.
w2 – проекция силы G
w3 – сила трения м-ла о лопасть.
![]()
w4 – сила трения о лопасть, обусловленная силой тяж.
![]()
![]()
Работа, кот произведут эти силы:
![]()
После интегрирования:
![]()
Формула для расчёта мощности с учётом размера лопасти:
![]()
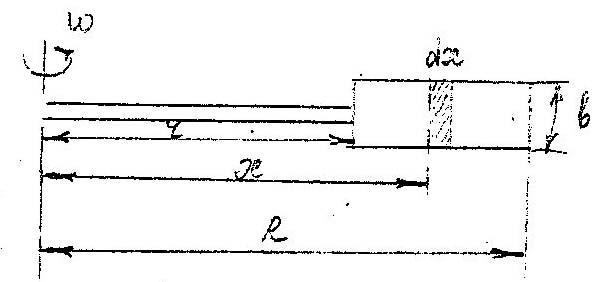
n – число оборотов в минуту (частота вращения)
z – число роторов
![]() -
удельный вес смеси
-
удельный вес смеси
З-н Ньютона для движения тв. тел в ж-ти
![]() ; с
– коэф. вязкости.
; с
– коэф. вязкости.
v – скорость движения вала
![]() -
производительность по площади
-
производительность по площади
![]() ;
; ![]() ;
;
![]()
![]()
Определение мощности:
![]()
Общая мощность:
![]() ; к-
КПД привода смесителя.
; к-
КПД привода смесителя.
Расчёт смесителя барабанного типа
В зависимости от степени заполнения барабанные смесители работают в 3-х разл режимах:
1). При степени заполнения до 3% мат-л колеб. движения, т.к. скользит по поверхности барабана как единое целое без перемешивания.
2). При степени заполнения от 3 до 10% сыпучий материал скользит по поверхности барабана как одно целое, оставаясь неподвижным в сост. равновесия на некотором достигнутом уровне.
3).
При степени заполнения > 10% сыпучий
материал непрерывно обрушивается и
перемешивается. При вращении барабана
центр тяжести материала поднимается
на некоторый угол
![]() .
На такой же угол поднимается по отношению
его свободная поверхность. Если
.
На такой же угол поднимается по отношению
его свободная поверхность. Если
![]() <
угла естественного откоса, то обрушения
не происходит. Но как только он его
превышает – происходит обрушение, что
способствует перераспределению частиц
в плоскости сегмента. В этом режиме
работают барабанные смесители.
<
угла естественного откоса, то обрушения
не происходит. Но как только он его
превышает – происходит обрушение, что
способствует перераспределению частиц
в плоскости сегмента. В этом режиме
работают барабанные смесители.
Не рекомендуется заполнение барабана более 30%
Ц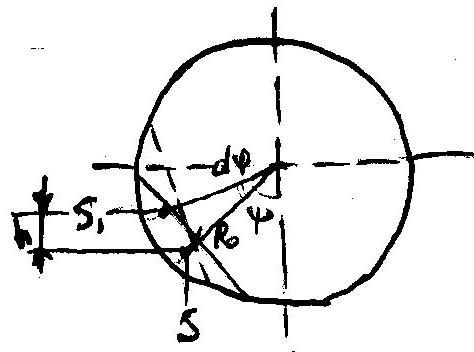 ентр
тяжести перемещается по дуге
ентр
тяжести перемещается по дуге
![]()
Допустим,
что длина дуги из-за малости угла
![]() равна
длине прямой
равна
длине прямой
![]()
![]() ;
; ![]()
![]() ;
; ![]() - работа
- работа
![]() - мощность
- мощность
![]()
![]()
