Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего

профессионального образования

«Тобольская государственная социально-педагогическая академия

им. Д.И. Менделеева»

Кафедра математики, ТиМОМ

Некоторые диофантовы уравнения

Курсовая работа

студента III курса ФМФ

Матаева Евгения Викторовича

Научный руководитель:

к.ф.-м.н. Валицкас А.И.

Оценка: ____________

Тобольск – 2011

Содержание

Введение……………………………………………………………………........2

§ 1. Линейные диофантовы уравнения…………………………………..3

§ 2. Диофантово уравнение x² – y² = a………………………………….....9

§ 3. Диофантово уравнение x² + y² = a…………………………………... 12

§ 4. Уравнение х²+ х + 1 = 3у²…………………………………………….. 16

§ 5. Пифагоровы тройки………………………………………………….. 19

§ 6. Великая теорема Ферма………………………………………………23

Заключение……………………………………………………………….….....29

Список литературы...........………………………………………………..30

ВВЕДЕНИЕ

Диофантово уравнение – это уравнение вида P(x₁ , … , x_n) = 0, где левая часть представляет собой многочлен от переменных x₁ , … , x_n с целыми коэффициентами. Любой упорядоченный набор (u₁ ; … ; u_n) целых чисел со свойством P(u₁ , … , u_n) = 0 называется (частным) решением диофантова уравнения P(x₁ , … , x_n) = 0. Решить диофантово уравнение – значит найти все его решения, т.е. общее решение этого уравнения.

Нашей целью будет научиться находить решения некоторых диофантовых уравнений, если эти решения имеется.

Для этого, необходимо ответить на следующие вопросы:

а. Всегда ли диофантово уравнение имеет решение, найти условия существования решения.

б. Имеется ли алгоритм, позволяющий отыскать решение диофантова уравнения.

Примеры: 1. Диофантово уравнение 5x – 1 = 0 не имеет решений.

2. Диофантово уравнение 5x – 10 = 0 имеет решение x = 2, которое является единственным.

3. Уравнение ln x – 8x² = 0 не является диофантовым.

4. Часто уравнения вида P(x₁ , … , x_n) = Q(x₁ , … , x_n), где P(x₁ , … , x_n), Q(x₁ , … , x_n) – многочлены с целыми коэффициентами, также называют диофантовыми. Их можно записать в виде P(x₁ , … , x_n) – Q(x₁ , … , x_n) = 0, который является стандартным для диофантовых уравнений.

5. x² – y² = a – диофантово уравнение второй степени с двумя неизвестными x и y при любом целом a. Оно имеет решения при a = 1, но не имеет решений при a = 2.

§ 1. Линейные диофантовы уравнения

Пусть a₁ , … , a_n , с Z . Уравнение вида a₁x₁ + … + a_nx_n = c называется линейным диофантовым уравнением с коэффициентами a₁ , … , a_n , правой частью c и неизвестными x₁ , … , x_n . Если правая часть с линейного диофантова уравнения нулевая, то такое диофантово уравнение называется однородным.

Наша ближайшая цель – научиться находить частные и общие решения линейных диофантовых уравнений с двумя неизвестными. Очевидно, что любое однородное диофантово уравнение a₁x₁ + … + a_nx_n = 0 всегда имеет частное решение (0; … ; 0).

Очевидно, что линейное диофантово уравнение, все коэффициенты которого равны нулю, имеет решение только в случае, когда его правая часть равна нулю. В общем случае имеет место следующая

Теорема (о существовании решения линейного диофантова уравнения). Линейное диофантово уравнение a₁x₁ + … + a_nx_n = c , не все коэффициенты которого равны нулю, имеет решение тогда и только тогда, когда НОД(a₁ , … , a_n) | c.

Доказательство. Необходимость условия очевидна: НОД(a₁ , … , a_n) | a_i (1 i n), так что НОД(a₁ , … , a_n) | (a₁x₁ + … + a_nx_n), а значит, делит и

c = a₁x₁ + … + a_nx_n .

Пусть D = НОД(a₁ , … , a_n), с = Dt и a₁u₁ + … + a_nu_n = D – линейное разложение наибольшего общего делителя чисел a₁ , … , a_n . Умножая обе части на t, получим a₁(u₁t) + … + a_n(u_nt) = Dt = c, т.е. целочисленная

n-ка (x₁t; … ; x_nt) является решением исходного уравнения с n неизвестными.

Теорема доказана.

Эта теорема даёт конструктивный алгоритм для нахождения частных решений линейных диофантовых уравнений.

Примеры: 1. Линейное диофантово уравнение 12x+21y = 5 не имеет решений, поскольку НОД(12, 21) = 3 не делит 5.

2. Найти частное решение диофантова уравнения 12x+21y = 6.

Очевидно, что теперь НОД(12, 21) = 3 | 6, так что решение существует. Запишем линейное разложение НОД(12, 21) = 3 = 122 + 21(–1). Поэтому пара (2; –1) – частное решение уравнения 12x+21y = 3, а пара (4; –2) – частное решение исходного уравнения 12x+21y = 6.

3. Найти частное решение линейного уравнения 12x + 21y – 2z = 5.

Так как (12, 21, –2) = ((12, 21), –2) = (3, –2) = 1 | 5, то решение существует. Следуя доказательству теоремы, вначале найдём решение уравнения (12,21)х–2у=5, а затем, подставив линейное разложение наибольшего общего делителя из предыдущей задачи, получим решение исходного уравнения.

Для решения уравнения 3х – 2у = 5 запишем линейное разложение НОД(3, –2) = 1 = 31 – 21 очевидно. Поэтому пара чисел (1; 1) является решением уравнения 3x – 2y = 1, а пара (5; 5) – частным решением диофантова уравнения 3х – 2у = 5.

Итак, (12, 21)5 – 25 = 5. Подставляя сюда найденное ранее линейное разложение (12, 21) = 3 = 122 + 21(–1), получим (122+21(–1))5 – 25 = 5, или 1210 + 21(–5) – 25 = 5, т.е. тройка целых чисел (10; –5; 5) является частным решением исходного диофантова уравнения 12x + 21y – 2z = 5.

Теорема (о структуре общего решения линейного диофантова уравнения). Для линейного диофантова уравнения a₁x₁ + … + a_nx_n = c справедливы следующие утверждения:

(1) если = (u₁ ; … ; u_n), = (v₁ ; … ; v_n) – его частные решения, то разность (u₁ – v₁ ; … ; u_n – v_n) – частное решение соответствующего однородного уравнения a₁x₁ + … + a_nx_n = 0,

(2) множество частных решений линейного диофантова однородного уравнения a₁x₁ + … + a_nx_n = 0 замкнуто относительно сложения, вычитания и умножения на целые числа,

(3) если M – общее решение данного линейного диофантова уравнения, а L – общее решение соответствующего ему однородного диофантова уравнения, то для любого частного решения = (u₁ ; … ; u_n) исходного уравнения верно равенство M = + L .

Доказательство. Вычитая равенство a₁v₁ + … + a_nv_n = c из равенства a₁u₁ + … + a_nu_n = c, получим a₁(u₁ – v₁) + … + a_n(u_n – v_n) = 0, т. е. набор

(u₁ – v₁ ; … ; u_n – v_n) – частное решение линейного однородного диофантова уравнения a₁x₁ + … + a_nx_n = 0. Таким образом, доказано, что

= (u₁ ; … ; u_n), = (v₁ ; … ; v_n) M L .

Это доказывает утверждение (1).

Аналогично доказывается утверждение (2):

,L z Z L z L .

Для доказательства (3) вначале заметим, что M + L. Это следует из предыдущего: M+L .

Обратно, если = (l₁ ; … ; l_n) L и = (u₁ ; … ; u_n) M, то M:

a₁(u₁ + l₁)+ …+a_n(u_n + l_n) = (a₁u₁ + … + a_nu_n)+(a₁l₁ + … + a_nl_n) = c + 0 = c.

Таким образом, + L M, и в итоге M = + L .

Теорема доказана.

Доказанная теорема имеет наглядный геометрический смысл. Если рассмотреть линейное уравнение a₁x₁ + … + a_nx_n = c, где х_i R, то как известно из геометрии, оно определяет в пространстве Rⁿ гиперплоскость, полученную из плоскости L c однородным уравнением a₁x₁+ … +a_nx_n=0, проходящей через начало координат, сдвигом на некоторый вектор Rⁿ. Поверхность вида + L называют также линейным многообразием с направляющим пространством L и вектором сдвига . Таким образом, доказано, что общее решение М диофантова уравнения a₁x₁ + … + a_nx_n = c состоит из всех точек некоторого линейного многообразия, имеющих целые координаты. При этом координаты вектора сдвига тоже целые, а множество L решений однородного диофантова уравнения a₁x₁ + … + a_nx_n = 0 состоит из всех точек направляющего пространства с целыми координатами. По этой причине часто говорят, что множество решений произвольного диофантова уравнения образует линейное многообразие с вектором сдвига и направляющим пространством L.

Пример: для диофантова уравнения х – у = 1 общее решение M имеет вид (1+у; у), где у Z, его частное решение = (1; 0), а общее решение L однородного уравнения х – у = 0 запишется в виде (у; у), где у Z . Таким образом, можно нарисовать следующую картинку, на которой решения исходного диофантова уравнения и соответствующего однородного диофантова уравнения изображены жирными точками в линейном многообразии М и пространстве L соответственно.

2. Найти общее решение диофантова уравнения 12x + 21y – 2z = 5.

Частное решение (10; –5; 5) этого уравнения было найдено ранее, найдём общее решение однородного уравнения 12x + 21y – 2z = 0, эквивалентного диофантову уравнению 12x + 21y = 2z.

Для разрешимости этого уравнения необходимо и достаточно выполнение условия НОД(12, 21) = 3 | 2z, т.е. 3 | z или z = 3t для некоторого целого t. Сокращая обе части на 3, получим 4x + 7y = 2t. Частное решение (2; –1) диофантова уравнения 4x + 7y = 1 найдено в предыдущем примере. Поэтому (4t ; –2t) – частное решение уравнения 4x + 7y = 2t при любом

t Z. Общее решение соответствующего однородного уравнения

(7u ; –4u) уже найдено. Таким образом, общее решение уравнения 4x + 7y = 2t имеет вид: (4t + 7u ; –2t – 4u), а общее решение однородного уравнения 12x + 21y – 2z = 0 запишется так:

(4t + 7u ; –2t – 4u ; 3t).

Нетрудно убедиться, что этот результат соответствует сформулированной выше без доказательства теореме о решениях однородного диофантова уравнения а₁х₁ + … + а_nх_n = 0: если Р = , то Р и

(u; t)P – общее решение рассматриваемого однородного уравнения.

Итак, общее решение диофантова уравнения 12x + 21y – 2z = 5 выглядит так: (10 + 4t + 7u ; –5 – 2t – 4u ; 5 + 3t).

3. На примере предыдущего уравнения проиллюстрируем другой метод решения диофантовых уравнений от многих неизвестных, который состоит в последовательном уменьшении максимального значения модулей его коэффициентов.

12x + 21y – 2z = 5 12x + (102 + 1)y – 2z = 5

12x + y – 2(z – 10y) = 5

.

Таким образом, общее решение рассматриваемого уравнения можно записать и так: (x; 5 – 12x + 2u ; 50 – 120x + 21u), где x, u – произвольные целые параметры.

§ 2. Диофантово уравнение x² – y² = a

Примеры: 1. При a = 0 получаем бесконечное число решений: x = y или x = –y для любого y Z.

2. При a = 1 имеем x² – y² = 1 (x + y)(x – y) = 1. Таким образом, число 1 разложено в произведение двух целых множителей x + y и x – y (важно, что x, y – целые !). Поскольку у числа 1 всего два разложения в произведение целых множителей 1 = 11 и 1 = (–1)(–1), то получаем две возможности: .

3. Для a = 2 имеем x² – y² = 2 (x + y)(x – y) = 2. Действуя аналогично предыдущему, рассматриваем разложения

2=12=21=(–1)(–2)=(–2)(–1), составляем системы: , которые, в отличие от предыдущего примера, не имеют решений. Так что нет решений и у рассматриваемого диофантова уравнения x² – y² = 2.

4. Предыдущие рассмотрения наводят на некоторые выводы. Решения уравнения x² – y² = a находятся по разложению a = km в произведение целых чисел из системы . Эта система имеет целые решения тогда и только тогда, когда k + m и k – m чётны, т.е. когда числа k и m одной чётности (одновременно чётны или нечётны). Таким образом, диофантово уравнение x² – y² = a имеет решение тогда и только тогда, когда a допускает разложение в произведение двух целых множителей одной чётности. Остаётся только найти все такие a .

Теорема (об уравнении x² – y² = a). (1) Уравнение x² – y² = 0 имеет бесконечное множество решений .

(2) Любое решение уравнения получается имеет вид , где a = km – разложение числа a в произведение двух целых множителей одной чётности.

(3) Уравнение x² – y² = a имеет решение тогда и только тогда, когда a 2 (mod 4).

Доказательство. (1) уже доказано.

(2) уже доказано.

(3) () Пусть вначале диофантово уравнение x² – y² = a имеет решение. Докажем, что a 2 (mod 4). Если a = km – разложение в произведение целых чисел одной чётности, то при чётных k и m имеем k = 2l, m = 2n и a = km = 4ln 0 (mod 4). В случае же нечётных k, m их произведение a также нечётно, разность a – 2 нечётна и не делится на 4, т.е. снова

a 2 (mod 4).

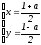() Если теперь a 2 (mod 4), то можно построить решение уравнения x² – y² = a. Действительно, если a нечётно, то a = 1a – разложение в произведение целых нечётных чисел, так что – решение диофантова уравнения. Если же a чётно, то ввиду a 2 (mod 4) получаем, что 4 | a, a = 4b = 2(2b) – разложение в произведение целых чётных чисел, так что – решение диофантова уравнения.

Теорема доказана.

Примеры: 1. Диофантово уравнение x² – y² = 2012 не имеет решений, т.к. 2010 = 4502 + 2 2 (mod 4).

2. Диофантово уравнение x² – y² = 2011 имеет решения, т.к.

2011 3 (mod 4). Имеем очевидные разложения

2011 = 12011 = 20111 = (–1)(–2011) = (–2011)(–1),

по каждому из которых находим решения 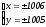(комбинации знаков любые). Других решений нет, т.к. число 2011 простое (?!).

§ 3. Диофантово уравнение x² + y² = a

Примеры: 1. 0 = 0² + 0², 1 = 0² + 1², k² = 0² + k². Таким образом, очевидно, любой квадрат тривиальным образом представим в виде суммы двух квадратов.

2. 2 = 1² + 1², 5 = 1² + 2², 8 = 2² + 2², 10 = 1² + 3², 13 = 2² + 3², 17 = 1² + 4², 18 = 3² + 3², 20 = 2² + 4², …

3. Решений нет для a = 3, 6 = 23, 7, 11, 12 = 2²3, 14 = 27, 15 = 35, 19, 21 = 37, 22 = 211, 23, 24 = 32³, …

Анализ приведённых результатов способен навести на мысль, что отсутствие решений каким-то образом связано с простыми числами вида

4n+3, присутствующими в разложении на множители чисел, не представимых в виде сумм двух квадратов.

Теорема (о представлении натуральных чисел суммами двух квадратов). Натуральное число a представимо в виде суммы двух квадратов тогда и только тогда, когда в его каноническом разложении простые числа вида 4n + 3 имеют чётные показатели степеней.

Доказательство. Вначале докажем, что если натуральное число a представимо в виде суммы двух квадратов, то в его каноническом разложении все простые числа вида 4n + 3 должны иметь чётные показатели степеней. Предположим, вопреки доказываемому, что a = р^2k+1b = x²+y², где

р – простое число вида 4n+3 и b p. Представим числа х и у в виде

х = Dz, y = Dt, где D = НОД(x, y) = р^sw, p w; z, t, s N₀ . Тогда получаем равенство р^2k+1b = D²(z² + t²) = р^2sw²(z² + t²) , т.е. р^2(k–s)+1b = w²(z² + t²). В левой части равенства присутствует p (нечётная степень не равна нулю), значит, на простое число p делится один из множителей в правой части. Поскольку p w, то р | (z² + t²), где числа z, t взаимно просты. Это противоречит следующей лемме (?!).

Лемма (о делимости суммы двух квадратов на простое число вида

4n + 3). Если простое число р = 4n+3 делит сумму квадратов двух натуральных чисел, то оно делит каждое из этих чисел.

Доказательство. От противного. Пусть x² +y²0(mod p), но x0(mod p) или y 0 (mod p). Поскольку x и y симметричны, их можно менять местами, так что можно предполагать, что x p.

Лемма (об обратимости по модулю p). Для любого целого числа x, не делящегося на простое число p, существует обратный элемент по модулю p – такое целое число 1 u < p, что xu 1 (mod p).

Доказательство. Число x взаимно простое с p, поэтому можно записать линейное разложение НОД(x, p) = 1 = xu + pv (u, v Z). Ясно, что xu1(modp), т.е. u – обратный элемент к x по модулю p. Если u не удовлетворяет ограничению 1 u < p, то поделив u с остатком на p, получим остаток r u (mod p), для которого xr xu 1 (mod p) и 0 r < p.

Лемма об обратимости по модулю p доказана.

Умножая сравнение x² + y² 0 (mod p) на квадрат u² обратного элемента к x по модулю p, получим 0 = 0u² x²u² + y²u² = (xu)² + (yu)² 1 + t² (mod p).

Таким образом, для t = yu выполнено сравнение t² –1 (mod p), которое и приведём к противоречию. Ясно, что t p : иначе t 0 (mod p) и 0 t² –1 (mod p), что невозможно. По теореме Ферма имеем t ^p–1 1 (mod p), что вместе с t² –1 (mod p) и p = 4n + 3 приводит к противоречию:

1 t ^p–1 = t ^4n+3–1 = t ^2(2n+1) = (t ²)²ⁿ⁺¹ (–1)²ⁿ⁺¹ = –1 (mod p).

Полученное противоречие показывает, что допущение о x 0 (mod p) было не верным.

Лемма о делимости суммы двух квадратов на простое число 4n+3 доказана.

Таким образом, доказано, что число, в каноническое разложение которого входит простое число p = 4n + 3 в нечётной степени, не представимо в виде суммы двух квадратов.

Докажем теперь, что любое число, в каноническом разложении которого простые числа p = 4n + 3 участвуют только в чётных степенях, представимо в виде суммы двух квадратов.

Идея доказательства основана на следующем тождестве:

(а² + b²)(c² + d²) = (ac – bd)² + (ad + bc)² ,

которое можно получить из известного свойства модуля комплексных чисел – модуль произведения равен произведению модулей. Действительно,

|z||t| = |zt| |a + bi||c + di| = |(a + bi)(c + di)|

|a + bi|²|c + di|² = |(ac – bd) + (ad + bc)i|²

(а² + b²)(c² + d²) = (ac – bd)² + (ad + bc)² .

Из этого тождества следует, что если два числа u, v представимы в виде суммы двух квадратов: u = x² + y², v = z² + t², то и их произведение uv представимо в виде суммы двух квадратов: uv = (xz – yt)² + (xt + yz)².

Любое натуральное число a > 1 можно записать в виде a = р₁ … р_km² , где р_i – попарно различные простые числа, m N. Для этого достаточно найти каноническое разложение 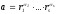, записать каждую степень вида r в виде квадрата (r)² при чётном = 2, или в виде r = r(r)² при нечётном = 2 + 1, а затем сгруппировать отдельно квадраты и оставшиеся одиночные простые числа. Например,

29250 = 23²5³13 = 2513(35)² , m = 15.

Число m² обладает тривиальным представлением в виде суммы двух квадратов: m² = 0² + m² . Если доказать представимость в виде суммы двух квадратов всех простых чисел р_i (1 i k), то используя тождество, будет получено и представление числа a. По условию, среди чисел р₁ , … , р_k могут встретиться только 2 = 1² + 1² и простые числа вида 4n + 1. Таким образом, осталось получить представление в виде суммы двух квадратов простого числа р = 4т + 1. Это утверждение выделим в отдельную теорему (см. ниже)

Например, для a = 29250 = 2513(15)² последовательно получаем:

2 = 1² + 1², 5 = 1² + 2², 13 = 2² + 3²,

25 = (11 – 12)² + (12 + 11)² = 1² + 3²,

2513 = (12 – 33)² + (13 + 32)² = 7² + 9²,

29250 = 2513(15)² = (715)² + (915)² = 105² + 135².

Теорема доказана.

§ 4. Уравнение х+ х + 1 = 3у

Займемся теперь уравнением х+x+1=Зу. Оно уже имеет свою историю. В 1950 г. Р. Облат высказал предположение, что, кроме решения

x=у=1. оно не имеет иных решений в натуральных числах х, у, где х есть нечетное число. В том же году Т. Нагель указал решение x = 313, у =181. Метод, аналогичный изложенному выше для уравнения х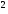+х-2у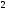=0, позволит нам определить все решения уравнения x+х+1=3у (1)

в натуральных числах x, у. Предположим, что (х, у) есть решение уравнения (1) в натуральных числах, причем х > 1. Можно легко убедиться, что уравнение(18) не имеет решений в натуральных числах x, у, где х = 2, 3. 4, 5, 6, 7, 8, 9; поэтому должно быть х10.

Покажем, что 12у<7x+3, 7у>4x + 2. 4у> 2x+1. (2)

Если бы было 12y>7x+3, мы имели бы 144у>49x+42x+9. а так как, в виду (18), 144у= 48x+ 48x + 48, то было бы х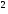< 6x +39, откуда

(х-З)<48 и, значит, учитывая, что x>10, 7<148, что невозможно. Итак, первое из неравенств (2) доказано.

Если бы было 7у < 4x+2, мы имели бы 49у< 16x+ 16x+4, а так как, ввиду (1), 16x+ 16x + 16 = 48у, то было бы 49у< 48у- 12, что невозможно. Таким образом, доказано второе из неравенств (2), из которого уже непосредственно вытекает третье. Итак, неравенства (2) верны.

Положим теперь

w = 7х — 12у+3, h = -4x + 7у-2. (3)

На основании (2), найдем, что w > 0, h > 0 и х — w=3(4y-2x-1)>0 и, значит, w<х. Согласно (3), имеем w²+w+1=3h² откуда, ввиду (1), Примем g(x, у) = (7х- 12у + 3, -4x + 7у -2).

Итак, можно сказать, что, исходя из любого решения (х, у) уравнения (1) в натуральных числах, где х > 1, мы получаем новое решение (w,h) = g(x, у) уравнения (1) в натуральных числах w,h где w < х (и значит, решение в меньших натуральных числах). Отсюда, действуя как выше, найдем, что для каждого решения уравнения (1) в натуральных числах х, у, где х > 1, существует натуральное число n такое, что g(x, y) = (l, 1).

Приняв же f(x, у) = (7x+12у + 3, 4x + 7у + 2), (4) легко найдем, что f(g(x,y)) = (x, у) и, следовательно, (x,y) = f(1,1) С другой стороны, легко проверить, что если (х, у) есть решение уравнения (1) в натуральных числах, то f(x,y) также есть решение уравнения (1) в натуральных числах (соответственно больших, чем х и у).

Приняв x=y=1(x, y) = f(1, 1) для n=2,3,…..,

получим последовательность {x,y}для n= 1, 2,….., содержащую все решения уравнения (1) в натуральных числах и только такие решения.

Здесь мы имеем (х,y)= f(1,1)=f(x, y),следовательно, в силу (4), получаем

х= 7x+12 y+3,y=4 x+7 y+2 (5) (n=1, 2, ...)

— формулы, позволяющие последовательно определять все решения (х, у) уравнения (1) в натуральных числах. Таким путем легко получаем решения (1,1),(22,13),(313,181),.(4366,2521),(60817,35113),..

Этих решений имеется, очевидно, бесконечное множество. Из равенств

х= у= 1и (4) при помощи индукции легко находим, что числа х с нечетными индексами суть нечетные, с четными же — четные, а числа yсуть нечетные для n = 1, 2, ... Для получения всех решений уравнения (1) в целых числах х, у, как нетрудно доказать, следовало бы к уже полученным решениям (x, y)присоединить (x, -y)и (-x-1, ±y)для n=1, 2, ...

Так что здесь мы имеем, например, еще такие решения: (—2,1) (—23,13), (—314,181). А. Роткевич заметил, что из всех решений уравнения (1) в натуральных числах х > 1 и у можно получить все решения уравнения (z+1)-z= y (6)

в натуральных числах z, у. В самом деле, допустим, что натуральные числа z,у удовлетворяют уравнению (5). Положив x=3z+l, получим, как легко проверить, натуральные числа х > 1 и у, удовлетворяющие уравнению (1).

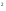С другой стороны, если натуральные числа х > 1 и у удовлетворяют уравнению (1), то имеем, как легко проверить, (х— 1)= 3(у-х), откуда следует, что число (натуральное) х—1 делится на 3, следовательно х-1= 3z, где z есть натуральное число, причем имеет место равенство 3z= y-x=у3z-1, которое доказывает, что числа z и у удовлетворяют уравнению (6). Таким образом, исходя из решений (22,13),(313,181), (4366,2521)уравнения (1), получаем решения (7,13),(104,181),(1455,2521) уравнения (6). Заметим здесь еще, что если натуральные числа z, у удовлетворяют уравнению (6), то доказано, что у есть сумма двух последовательных квадратов, например 13=2+3,181=9+10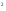, 2521=35+ 36. Подобным образом, как прежде для уравнения(1), мы могли бы найти все решения уравнения x+(x+1)=yв натуральных числах х, у, приняв для х > 3 g(x. у) = (3х -2у+1, 3у - 4х- 2) и для x> 1 f(x, y) = (3x + 2y+l, 4х + Зу + 2), что приводит к формуле (х, у) f(3,5) и к выводу, что все решения уравнения (6) в натуральных числах х, у содержатся в последовательности {x,y} для n= 1, 2,…., где х= 3, у= 5, аx=3x+2y+1. y = 4 x+3 y+2 (n=1, 2, ...). Например, х=3•3+2•5+1=20, у= 4•3+З•5 + 2 = 29;x=119, у=169:x=69б, у= 985;x=4059, у=5741.

Геометрический смысл рассмотренного уравнения состоит в том, что оно дает все пифагоровы треугольники (прямоугольные с натуральными сторонами), катеты которых выражаются последовательными натуральными числами. Таких треугольников имеется бесконечное множество (*).

Уравнение же x+(x+1)=y,как доказано, не имеет решений в натуральных числах х, у.