
- •6.3. Синхронна мережа Гопфілда
- •6.4. Неперервна мережа Гопфілда
- •6.5. Асоціативна мережа вsв
- •7. Синергетичний комп’ютер
- •8. Мережа хеммінга
- •9. Динамічні рекурсивні шнм
- •9.1. Структура дрм
- •9.2. Неперервні дрм
- •9.3. Дискретна дрм
- •9.3.2. Частково-рекурсивні мережі
- •9.3.3. Локально-рекурсивні мережі прямого поширення
- •9.4. Навчання дрм
- •9.4.1. Алгоритм зворотного поширення помилки
- •9.4.2. Адаптивний алгоритм навчання
- •10. Мережа векторного квантування
- •10.1. Структура мережі векторного квантування
- •10.2. Неконтрольоване навчання мережі вк
- •10.3. Контрольоване навчання мережі вк
- •10.3.1. Lvq1
- •10.3.2. Lvq2.1
10.2. Неконтрольоване навчання мережі вк
Існує кілька підходів до навчання мережі ВК. У найпростішому, початковому варіанті під час навчання відбувалася зміна ваг тільки нейрона-переможця відповідно до правила

тут а – коефіцієнт навчання.
Якщо
сума ваг для кожного нейрона є величиною
постійною й
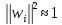 ,
а вхідні вектори нормалізовані|
,
а вхідні вектори нормалізовані|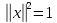 ,
то, як показав Когонен, час визначення
нейрона-переможця може бути скорочено.
При цьому нейрон-переможець с
визначається шляхом мінімізації
евклідової норми
,
то, як показав Когонен, час визначення
нейрона-переможця може бути скорочено.
При цьому нейрон-переможець с
визначається шляхом мінімізації
евклідової норми
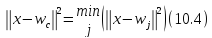
aбо
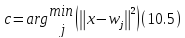
При виконанні зазначених вище умов щодо норм вхідних і вагових векторів
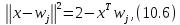
величина
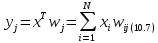
може
використовувався як критерій подібності
образів х
й

У дискретному випадку при поданні на кожному такті навчання нового вхідного образу відбувається корекція ваг нейрона-переможця за формулою
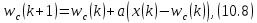
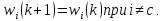
Як
і в (10.3), коефіцієнт навчання a може бути
обраний постійним або зменшуваним
у процесі навчання. Як випливає з (10.8),
вектор ваг нейрона-переможця
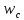 зміщується в напрямку вектора вхідного
образух.
Процес корекції ваг цього нейрона
зображено на рис. 10.3.
зміщується в напрямку вектора вхідного
образух.
Процес корекції ваг цього нейрона
зображено на рис. 10.3.
При
 вектор
вектор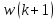 корегується
на величину
корегується
на величину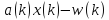 і
має нове розміщення
і
має нове розміщення .
Видно, що навчання полягає в обертанні
вагового вектора в напрямку вектора
входівх(k)
без істотної зміни його довжини.
.
Видно, що навчання полягає в обертанні
вагового вектора в напрямку вектора
входівх(k)
без істотної зміни його довжини.
Процес, відображений виразами (10.4), (10.5) і (10.8), описує послідовну корекцію векторів вагових коефіцієнтів, які в асимптотиці забезпечують практично оптимальне розбивання простору вхідних образів на кластери. Оптимальність тут розуміється в тому значенні, що внаслідок віднесення поданого образу до найближчого опорного представника при даному розбиванні кількість неправильно класифікованих образів буде мінімальною.
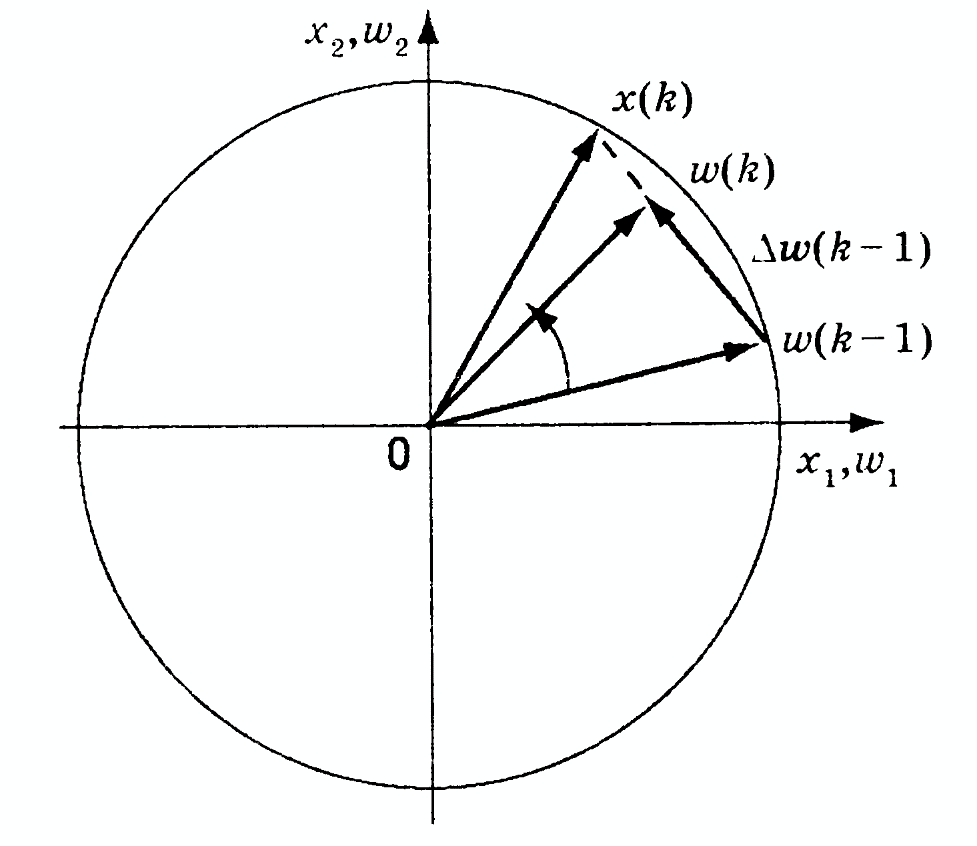
Рис. 10.3. Корекція ваг нейрона-переможця
Основним недоліком цього виду навчання є те, що якщо початкові розподіли векторів ваг і вхідних образів не є приблизно однаковими, то може виникнути ситуація, коли деякі з нейронів ніколи не стануть переможцями, тобто їхні вектори ваг не змінюватимуться. Для виключення подібної ситуації в алгоритм навчання вводять деякий механізм «пам’яті», що штрафує часто кореговані ваги нейронів-переможців. Як алгоритм навчання з «пам’яттю» може бути використаний, наприклад, такий:
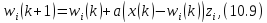
де
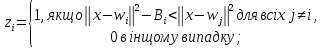
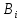 =
=
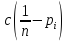 —
коефіцієнт штрафу;
—
коефіцієнт штрафу;
 —
часовий
інтервал, на якому і-й
нейрон є переможцем
—
часовий
інтервал, на якому і-й
нейрон є переможцем
 ;
;
b є (0,1] — постійний параметр;
с — постійний параметр, що впливає на величину штрафу.
Цей алгоритм навчання є більш ефективним, ніж (10.8). Однак сьогодні значного поширення отримали алгоритми корекції параметрів, в основі яких лежить контрольоване навчання.
10.3. Контрольоване навчання мережі вк
Основною відмінністю контрольованого навчання мережі ВК (Learning Vector Quantization, LVQ) від розглянутого вище є використання для кожного вхідного образу x бажаного відповідного вихідного сигналу. Цей вид навчання реалізується різними способами.
10.3.1. Lvq1
Як
і в описаному вище методі, переможцем
у мережі є той нейрон, вектор ваг
якого
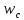 найближчий
до вхідного образу х,
тобто нейрон с визначається як
найближчий
до вхідного образу х,
тобто нейрон с визначається як

Значення
всіх ваг
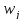 що мінімізують помилку класифікації,
обчислюютьсяLVQ1-методом
асимптотично. При цьому корекція ваг
відбувається за правилом
що мінімізують помилку класифікації,
обчислюютьсяLVQ1-методом
асимптотично. При цьому корекція ваг
відбувається за правилом
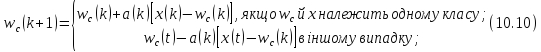
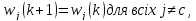
де
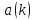 є
(0, 1]. Параметр
є
(0, 1]. Параметр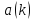 може залишатися постійним або монотонно
зменшуватися.
може залишатися постійним або монотонно
зменшуватися.
Таким
чином, вектор ваг нейрона-переможця
и)с,
що найближче розташований до поданого
вхідного вектора, зміщується в напрямку
останнього, якщо вхідний вектор
відноситься до одного з ним класу, і
віддаляється від нього в іншому випадку.
Ваги інших нейронів не змінюються. Зміну
ваг нейрона Когонена зображено на
рис. 10.4. На рис. 10.4, а
наведено випадок, коли вектори
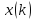 і
і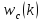 відносяться
до одного класу, на рис. 10.4,б
— до різного.
відносяться
до одного класу, на рис. 10.4,б
— до різного.
Приклад 10.1. Розглянемо роботу методу LVQ1 на прикладі навчання мережі, що складається з двох нейронів і класифікує вісім векторів, які відносяться до двох різних класів:
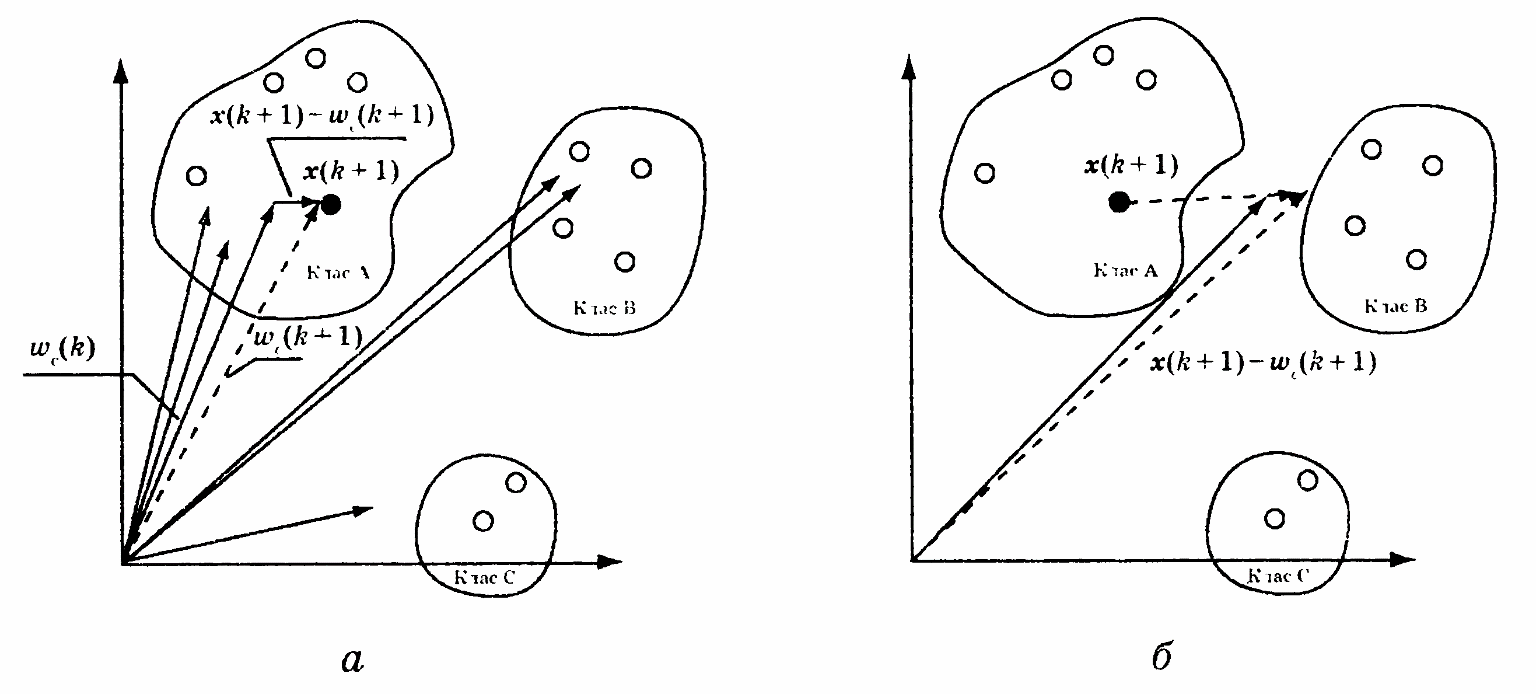
Рис. 10.4. Зміна ваг нейронів Когонена

Як
початкові значення векторів ваг
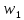 й
й ,
асоційованих із класами 1 й 2, приймемо
відповідно вектори
,
асоційованих із класами 1 й 2, приймемо
відповідно вектори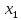 і
і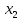 Навчання мережі здійснюватимемо за
алгоритмом (10.10) з а = 0,1.
Навчання мережі здійснюватимемо за
алгоритмом (10.10) з а = 0,1.
Розглянемо перший цикл навчання.
При
надходженні вектора
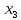 (з урахуванням того, що
(з урахуванням того, що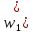 0)
=
0)
=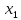 й
й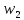 (0) =
(0) =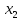 )
маємо
)
маємо
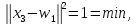
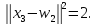
Оскільки
переможцем виявився перший нейрон, то
настроюємо його ваги, беручи до уваги,
що
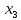 відноситься
до класу 1, тобто
відноситься
до класу 1, тобто
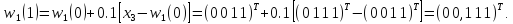
При
надходженні вектора
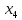 маємо
маємо
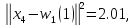
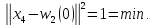
Тому
корегуємо ваги
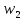 (0)
з
урахуванням того, що
(0)
з
урахуванням того, що
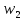 (0)
і
(0)
і
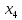 відносяться
до різних класів
відносяться
до різних класів
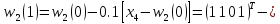
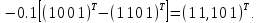
Аналогічно
отримуємо для
 :
:
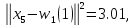
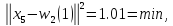
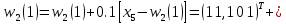
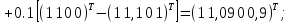
для
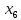 :
:
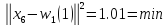
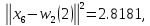
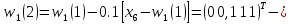
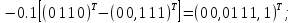
для
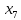 :
:
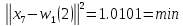
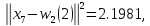
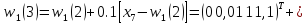
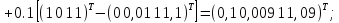
для
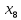 :
:

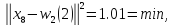
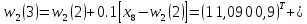
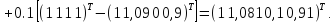
Перший цикл навчання завершено. Отримані значення векторів ваг
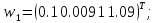
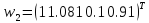
призводять
до того, що мережа відносить
 до
другого класу, а
до
другого класу, а
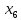 — до першого. Продовжуючи навчання
мережі, робимо висновок, що правильна
класифікація буде досягнута після 12
циклу. При цьому
— до першого. Продовжуючи навчання
мережі, робимо висновок, що правильна
класифікація буде досягнута після 12
циклу. При цьому
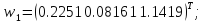
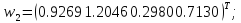
Після 500 циклів навчання з a = 0,1 отримаємо такі значення шуканих векторів ваг:
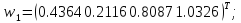
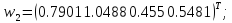
Неважко перевірити, що при даних вагах всі подані мережі вектори будуть класифіковані правильно.
