
- •1. Лекція: Початкові поняття теорії графів
- •Початкові поняття теорії графів
- •Визначення графа
- •Графи і бінарні відношення
- •Звідки беруться графи
- •Число графів
- •Суміжність, інцидентність, ступені
- •Деякі спеціальні графи
- •Графи і матриці
- •Зважені графи
- •Ізоморфізм
- •Інваріанти
- •Операції над графами
- •Локальні операції
- •Підграфи
- •Алгебраїчні операції
Суміжність, інцидентність, ступені
Якщо
в графі є ребро
![]() ,то
говорять, що вершини
,то
говорять, що вершини
![]() і
і![]() суміжні
в
цьому графі, ребро
суміжні
в
цьому графі, ребро
![]() інцидентне
кожній
з вершин
інцидентне
кожній
з вершин
![]() ,
,![]() ,а
кожна з них інцидентна
цьому
ребру.
,а
кожна з них інцидентна
цьому
ребру.
Множина
всіх вершин графа, суміжних з даною
вершиною
![]() називається
околом
цієї
вершини і позначається через
називається
околом
цієї
вершини і позначається через
![]() .
.
На
практиці зручним і ефективним при
вирішенні багатьох завдань способом
задання графа є так звані списки
суміжності. Ці списки можуть бути
реалізовані різними способами у вигляді
конкретних структур даних, але у
будь-якому випадку мова йде про те, що
для кожної вершини
![]() перераховуються
всі суміжні з нею вершини, тобто елементи
множини
перераховуються
всі суміжні з нею вершини, тобто елементи
множини
![]() .
Такий спосіб завдання дає можливість
швидкого перегляду околу вершини.
.
Такий спосіб завдання дає можливість
швидкого перегляду околу вершини.
Число
вершин, суміжних з вершиною
![]() називається
ступенем
вершини
називається
ступенем
вершини
![]() і
позначається через
і
позначається через
![]() .
.
Якщо скласти ступені всіх вершин деякого графа, то кожне ребро внесе до цієї суми внесок, рівний 2, тому справедливо наступне твердження:
Теорема
2.
![]() .
.
Ця рівність відома як "лема про рукостискання". З нього виходить, що число вершин непарного ступеня в будь-якому графові парне.
Вершину
ступеня
![]() називають
ізольованою.
називають
ізольованою.
Граф
називають регулярним
ступеня
![]() ,якщо
ступінь кожної його вершини рівна
,якщо
ступінь кожної його вершини рівна
![]() .
.
Набір ступенів графа – це послідовність ступенів його вершин, виписаних в неспадному порядку.
Деякі спеціальні графи
Розглянемо деякі особливо графи, що часто зустрічаються.
Порожній
граф – граф,
що не містить жодного ребра. Порожній
граф з множиною вершин
![]() позначається
через
позначається
через
![]() .
.
Повний
граф – граф,
в якому кожні дві вершини суміжні. Повний
граф з множиною вершин
![]() позначається
через
позначається
через
![]() .
.
Граф
![]() зокрема,
має одну вершину і жодного ребра. Очевидно
зокрема,
має одну вершину і жодного ребра. Очевидно
![]() .
Вважатимемо також, що існує граф
.
Вважатимемо також, що існує граф
![]() ,у
якого
,у
якого
![]() .
.
Ланцюг
(шлях)
![]() –граф
з множиною вершин
–граф
з множиною вершин
![]() і
множиною ребер
і
множиною ребер
![]() .
.
Цикл
![]() –граф,
який утворюється з графа
–граф,
який утворюється з графа
![]() додаванням
ребра
додаванням
ребра
![]() .
.
Всі
ці графи при
![]() показані
на рис. 1.6
показані
на рис. 1.6
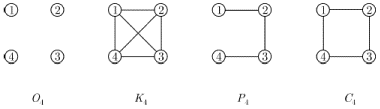
Рис. 1.6.
Графи і матриці
Хай
![]() -
граф з
-
граф з
![]() вершинами,
причому
вершинами,
причому
![]() .
Побудуємо квадратну матрицю
.
Побудуємо квадратну матрицю
![]() порядку
порядку
![]() ,у
якій елемент
,у
якій елемент
![]() ,що
стоїть на перетині рядка з номером
,що
стоїть на перетині рядка з номером
![]() і
стовпця з номером
і
стовпця з номером
![]() ,визначається
таким чином:
,визначається
таким чином:
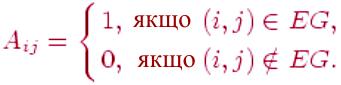
Вона
називається матрицею
суміжності графа.
Матрицю суміжності можна побудувати і
для орієнтованого графа, і для
неорієнтованого, і для графа з петлями.
Для звичайного графа вона володіє двома
особливостями: через відсутність петель
на головній діагоналі стоять нулі, а
оскільки граф неорієнтований, то матриця
симетрична щодо головної діагоналі. І
навпаки, кожній квадратній матриці
порядку
![]() ,складено
з нулів і одиниць і такої, що володіє
двома вказаними властивостями, відповідає
звичайний граф з множиною вершин
,складено
з нулів і одиниць і такої, що володіє
двома вказаними властивостями, відповідає
звичайний граф з множиною вершин
![]() .
.
Інша
матриця, що асоціюється з графом, – це
матриця
інцидентності.
Для її побудови занумеруємо вершини
графа числами від 1 до
![]() ,а
ребра – числами від 1 до
,а
ребра – числами від 1 до
![]() .
Матриця інцидентності
.
Матриця інцидентності
![]() має
має
![]() рядків
і
рядків
і
![]() стовпців,
а її елемент
стовпців,
а її елемент
![]() рівний
1, якщо вершина з номером
рівний
1, якщо вершина з номером
![]() інцидентна
ребру з номером
інцидентна
ребру з номером
![]() ,інакше
він рівний нулю. На рис. 1.7 показаний
граф із занумерованими вершинами і
ребрами і його матриці суміжності і
інцидентності.
,інакше
він рівний нулю. На рис. 1.7 показаний
граф із занумерованими вершинами і
ребрами і його матриці суміжності і
інцидентності.
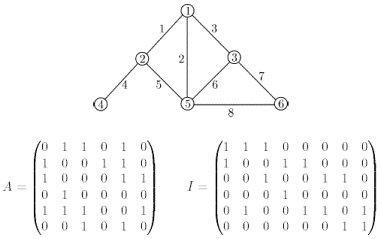
Рис. 1.7.
Для
орієнтованого графа матриця інцидентності
визначається трохи інакше: її елемент
![]() рівний
1, якщо вершина
рівний
1, якщо вершина
![]() є
початком ребра
є
початком ребра
![]() і
рівний
і
рівний
![]() ,якщо
вона є кінцем цього ребра, і він рівний
,якщо
вона є кінцем цього ребра, і він рівний
![]() ,якщо
ця вершина і це ребро не інцидентні один
одному.
,якщо
ця вершина і це ребро не інцидентні один
одному.
