Планарні графи

Геометричний граф – це плоска фігура, що складається з вершин – точок площини і ребер – ліній, що сполучають деякі пари вершин. Всякий граф можна багатьма способами представити геометричним графом, і ми вже не раз користувалися цією можливістю. На рис. 4.6 показано два геометричних графи і , що представляють, як неважко перевірити, один і той же звичайний граф. Просту будову цього графу, очевидну на зображенні зліва, не так легко виявити, розглядаючи зображення справа. Головна причина цього в тому, що в ребра не мають "зайвих" перетинів.

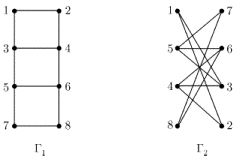
Рис. 3.6.

Геометричний граф, в якому жодні два ребра не мають загальних точок, окрім інцидентної їм обом вершини, називають плоским графом, а по відношенню до представляємого ним звичайного графу – його плоскою укладкою. Не кожен граф допускає плоску укладку. Граф, для якого існує плоска укладка, називається планарним графом. Окрім зручності візуального аналізу, є немало причин, у тому числі і суто практичних, для інтересу до планарних графів і їх плоских укладок.

Якщо площину розрізати по ребрах плоского графа, вона розпадеться на зв'язні частини, які називають гранями. Завжди є одна необмежена зовнішня грань, всі решта грані називаються внутрішніми. Якщо в плоскому графові немає циклів, то у нього є лише одна грань. Якщо ж цикли є, то кордон кожної грані містить цикл, але не обов'язково є циклом. На рис. 3.7 показаний плоский граф з п'ятьма пронумерованими гранями. Кордон грані з номером 3 складається з двох циклів, а кордон грані з номером 2 окрім циклу довжини 5 включає ще дерево з трьох ребер.

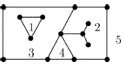
Рис. 4.7.

Множина ребер, яка створює кордони граней, може бути різною для різних плоских укладок одного і того ж графа. На рис. 4.8 показано дві плоскі укладки одного графу. У лівій укладці є дві грані, кордони яких є простими циклами довжини 5. У правій укладці таких граней немає, але є грані, обмежені циклами довжини 4 і 6. Проте число граней, як показує наступна теорема, не залежить від укдки, тобто є інваріантом планарного графу.

Мал. 3.8.

Теорема 6 (формула Ейлера). Кількість граней в будь-якій плоскій укладці планарного графу, що має вершин, ребер і компонентів зв'язності, рівна .

Доведення.

Доведемо спочатку твердження теореми при . Розглянемо зв'язний плоский граф . Якщо в ньому немає циклів, то є єдина грань, а , і формула вірна. Якщо ж є хоч би один цикл, то візьмемо яке-небудь ребро , що належить простому циклу . Це ребро належить кордону двох граней, одна з яких цілком лежить всередині циклу , інша – зовні. Якщо видалити ребро з графа, ці дві грані зіллються в одну. Граф , отриманий з графу видаленням ребра , вочевидь, буде плоским і зв'язним, в ньому на одне ребро і на одну грань менше, ніж в , а число вершин залишилося тим самим. Якщо в ще є цикли, то, видаливши ще одне циклове ребро, отримаємо граф . Продовжуватимемо видалення циклових ребер до тих пір, поки не вийде зв'язний плоский граф без циклів, тобто дерево. У нього ребро і єдина грань. Значить, всього було видалено ребер, а оскільки при видаленні кожного ребра число граней зменшувалося на одиницю, то у вихідному графові було грані. Таким чином, формула вірна для будь-якого зв'язкового плоского графа. Якщо граф незв'язний, то в компоненті зв'язності, що має вершин і ребер, як доведено вище, буде внутрішня грань. Підсумовуючи по всіх компонентах і додаючи 1 для врахування зовнішньої грані, переконуємося в справедливості формули в загальному випадку.

Наслідок 1. Якщо в планарному графові вершин, , і ребер, то .

Доведення.

Якщо в графі немає циклів, то і нерівність виконується при . Розглянемо плоский граф з гранями, в якому є цикли. Пронумеруємо грані числами від 1 до і позначимо через кількість ребер, що належать грані з номером і. Оскільки кордон кожної грані містить цикл, то для кожного і, отже . З іншого боку, кожне ребро належить кордону не більше ніж двох граней, тому . З цих двох нерівностей виходить, що . Застосовуючи формулу Ейлера, отримуємо .

Наслідок 1 дає необхідну умову планарності, яка в деяких випадках дозволяє встановити, що граф не є планарним. Розглянемо, наприклад, повний граф . У нього , , і ми бачимо, що нерівність із наслідку 1 не виконується. Значить, цей граф непланарний. В той же час існують графи, що не є планарними, для яких нерівність наслідку 1 виконується. Приклад – повний дводольний граф . У нього 6 вершин і 9 ребер. Нерівність виконується, але ми зараз встановимо, що він непланрний. Відмітимо, що в цьому графові немає циклів довжини 3 (оскільки він дводольний, в ньому взагалі немає циклів непарної довжини). Тому кордон кожної грані містить не менше чотирьох ребер. Повторюючи міркування з доведення наслідку 1, але використовуючи нерівність замість , отримуємо наступний результат:

Наслідок 2. Якщо в планарному графові вершин, , ребер і немає циклів довжини 3, то .

Для графа нерівність наслідку 2 не виконується, і це доводить, що він непланарний.

Відомо декілька критеріїв планарності, сформулюємо без доведення два з них. Два графи називають гомеоморфними, якщо з них за допомогою підрозбиття ребер можна отримати ізоморфні графи. На рис. 4.9 намальовані гомеоморфні графи.

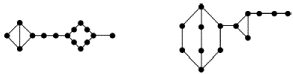
Рис. 4.9.

Сформулюємо без доведення два критерії планарності.

Теорема 7 (критерій Понтрягіна-Куратовського). Граф планарний тоді і лише тоді, коли у нього немає підграфів, гомеоморфних або .

Граф називається стягуваним до графу , якщо можна отримати з послідовністю операцій стягування ребер.

Теорема 8 (критерій Вагнера). Граф планарний тоді і лише тоді, коли у нього немає підграфів, що стягуються до або .

Зазначимо, що, не дивлячись на зовнішню схожість двох теорем, поняття гомеоморфізму і стягуваності, що фігурують в них, істотно розрізняються. На рис. 4.10 намальований граф, який називають графом Петерсена. У ньому немає підграфу, гомеоморфного , оскільки в графові кожна вершина має ступінь 4, а в графові Петерсена ступінь кожної вершини рівна 3. При видаленні вершин і ребер і підрозбитті ребер ступені вершин не збільшуються. В той же час легко бачити, що граф Петерсена можна перетворити на стягуванням п'яти ребер.

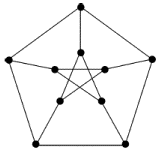
Рис. 4.10.