Каркаси

Хай –звичайний граф. Його каркасом називається остовный підграф, в якому немає циклів, а області зв'язності збігаються з областями зв'язності графа . Таким чином, каркас зв'язного графу – дерево, а в загальному випадку – ліс.

У будь-якого графа є хоч би один каркас. Дійсно, якщо в немає циклів, то він сам є власним каркасом. Якщо ж цикли є, то можна видалити з графа будь-яке ребро, що належить якому-небудь циклу. Таке ребро не є перешийком, тому при його видаленні області зв'язності не зміняться. Продовжуючи діяти таким чином, після видалення деякої кількості ребер отримаємо остовний підграф, в якому циклів вже немає, а області зв'язності – ті ж, що у вихідного графа, тобто цей підграф і буде каркасом. Можна навіть точно сказати, скільки ребер необхідно видалити для здобуття каркасу. Якщо в графі вершин, ребер і компонент зв'язності, то в каркасі буде теж вершин і компонент зв'язності. Але в будь-якому лісі з вершинами і компонентами зв'язності є рівно ребер. Значить, видалено буде ребер. Це число називається цикломатичним числом графа і позначається через .

Якщо в графі є цикли, то у нього більше одного каркасу. Визначити точне число каркасів зв'язного графа дозволяє так звана матрична теорема Кірхгофа. Приведемо її без доведення. Для графа визначимо матрицю – квадратну матрицю порядку з елементами

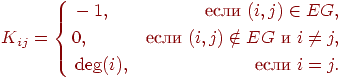
Інакше кажучи, виходить з матриці суміжності, якщо замінити всі 1 на -1, а замість нулів на головній діагоналі поставити ступені вершин. Відмітимо, що матриця – вироджена, оскільки сума елементів кожного рядка рівна 0, тобто стовпці лінійно залежні.

Теорема 4 (матрична теорема Кірхгофа). Якщо – зв'язний граф з не менше, ніж двома вершинами, то алгебраїчні доповнення всіх елементів матриці рівні між собою і дорівнюють числу каркасів графа .

Дводольні графи

Граф називається дводольним, якщо множину його вершин можна так розбити на дві підмножини, аби кінці кожного ребра належали різним підмножинам. Ці підмножини називаються долями. Таким чином, кожна з доль породжує порожній підграф. Прикладом дводольного графа є простий ланцюг при будь-якому : одна доля породжується вершинами з парними номерами, інша – з непарними. Граф – приклад графа, що не є дводольним: при будь-якому розбитті множини його вершин на дві підмножини в одній з цих підмножин виявляться дві суміжні вершини.

Прикладне значення поняття дводольного графа пов'язане з тим, що за допомогою таких графів моделюються відношення між об'єктами двох типів, а такі стосунки часто зустрічаються на практиці (наприклад, відношення "продукт використовується у виробництві виробу " між вихідними продуктами і готовими виробами, або "працівник володіє професією " між працівниками і професіями). У математиці такі стосунки теж нерідкі, один з найбільш поширених їх видів – відношення інцидентності. Хай – множина, а – сімейство його підмножин. Елемент і множина інцидентні один одному, якщо . Відношення інцидентності можна описати за допомогою дводольного графа, в якому ,. На рис. 4.3 показаний граф відношення інцидентності для, , де,,,.

Рис. 3.3.

Взагалі кажучи, розбиття множини вершин дводольного графу на долі можна здійснити не єдиним способом. Так, в графі з тільки що наведеного прикладу можна взяти за долі множину і. В той же час в самому визначенні цього графу вже закладено "природне" розбиття на долі і . Дводольні графи, що виникають в додатках, часто бувають задані саме так – з множиною вершин, що спочатку складається з двох частин, і з множиною ребер, кожне з яких сполучає вершини з різних частин.

Якщо розбиття на долі не задане, то може виникнути питання, чи існує воно взагалі, тобто чи є даний граф дводольним? Якщо в графі вершин, то є розбиття множини вершин на дві підмножини і безпосередня перевірка всього цього розбиття буде дуже трудомісткою справою. Наступна теорема дає критерій дводольності, а з її доведення можна отримати і ефективний алгоритм перевірки дводольності. Детально такий алгоритм буде описаний в наступному занятті.

Теорема 5. Наступні твердження для графа рівносильні:

• (1) - дводольний граф;

• (2) у немає циклів непарної довжини;

• (3) у немає простих циклів непарної довжини.

Доведення.

Доведемо, що з (1) слідує (2). Хай – дводольний граф, в якому вибрано деяке розбиття на долі, – цикл довжини в графі . При будь-якому вершини і суміжні і, отже, належать різним долям. Таким чином, одна доля складається зі всіх вершин з непарними індексами, тобто , інша – зі всіх вершин з парними індексами. Але вершини ітеж суміжні і повинні належати різним долям. Отже, – парне число.

Вочевидь, що з (2) слідує (3); залишається довести, що з (3) слідує (1). Розглянемо граф , в якому немає простих циклів непарної довжини. Ясно, що граф, в якому кожна компонента зв'язності – дводольний граф, сам дводольний. Тому можна вважати, що граф зв'язний. Зафіксуємо в ньому деяку вершину і доведемо, що для будь-яких двох суміжних між собою вершин і має місце рівність . Дійсно, допустимо спочатку, що . Хай – найкоротший шлях з в – найкоротший шлях з в . Ці шялхи починаються в одній вершині: , а закінчуються в різних:, . Тому знайдеться таке , що і при всіх . Але тоді послідовність є простим циклом довжини . Отже, . Вважатимемо, що . Якщо – найкоротший шлях з в , то, вочевидь, що – найкоротший шлях з в , отже . Отже, відстані від двох суміжних вершин до вершини розрізняються рівно на одиницю. Тому, якщо позначити через множину всіх вершин графу, відстань від яких до вершини парна, а через множину всіх вершин з непарними відстанями до , то для кожного ребра графу один з його кінців належить множині , інший – множині . Отже, граф – дводольний.

Хай – цикл в графі . Множина вершин циклу породжує в підграф, який містить всі ребра цього циклу, але може містити і ребра, що йому не належать. Такі ребра називають хордами циклу . Простий цикл, що не має хорд, – це породжений простий цикл. У графові, зображеному на рис. 4.4, хордами циклу є ребра, ,і, а цикл – породжений простий цикл. Відмітимо, що будь-який цикл довжини 3 є породженим простим циклом.

Рис. 4.4.

Хай – простий цикл довжини в деякому графові, – хорда цього циклу. Ребро разом з ребрами циклу утворює два цикли меншої довжини, і(див. рис. 4.5), сума довжин яких рівна.

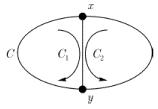
Рис. 4.5.

Значить, якщо – цикл непарної довжини, то один з циклів ітеж має непарну довжину. Звідси витікає, що в графові, в якому є цикл непарної довжини, є і породжений простий цикл непарної довжини. Тому критерій дводольності справедливий і в наступному формулюванні.

Наслідок. Граф є дводольним тоді і лише тоді, коли в ньому немає породжених простих циклів непарної довжини.