
Найважливіші класи графів
Дерева. Центр дерева. Кореневі дерева. Каркаси. Дводольні графи. Планарні графи.
![]()
Дерева
Деревом називається зв'язний граф, що не має циклів. У графі без циклів, таким чином, кожна компонента зв'язності є деревом. Такий граф називають лісом.
З
теореми 2 лекції 3 витікає, що у всякому
дереві, в якому не менше двох вершин, є
вершина міри 1. Такі вершини називають
висячими вершинами, або листям. Насправді
легко довести, що в кожному дереві не
менше двох листів, а ланцюг ![]() – приклад дерева, в якому точно два
листи.
– приклад дерева, в якому точно два
листи.
У наступних двох теоремах встановлюються деякі властивості дерев.
Теорема
1. Граф з ![]() вершинами і
вершинами і ![]() ребрами є деревом тоді і лише тоді, коли
він задовольняє будь-яким двом з наступних
трьох умов:
ребрами є деревом тоді і лише тоді, коли
він задовольняє будь-яким двом з наступних
трьох умов:
(1) зв'язний;
(2) не має циклів;
(3)
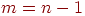 .
.
Доведення.
Перші дві умови разом складають визначення дерева. Покажемо, що виконання будь-яких двох з умов (1) -(3) спричиняє за собою виконання третього.
(1)
і (2) ![]() (3). Індукція по числу вершин. При
(3). Індукція по числу вершин. При ![]() твердження очевидне. При
твердження очевидне. При ![]() в дереві є хоч би один лист. Якщо з дерева
видалити лист, то знову вийде дерево,
оскільки циклів не з'явиться, а зв'язність,
вочевидь, збережеться. У цьому новому
дереві
в дереві є хоч би один лист. Якщо з дерева
видалити лист, то знову вийде дерево,
оскільки циклів не з'явиться, а зв'язність,
вочевидь, збережеться. У цьому новому
дереві ![]() вершин і, по припущенню індукції,
вершин і, по припущенню індукції, ![]() ребра. Отже, у вихідному дереві було
ребра. Отже, у вихідному дереві було ![]() ребро.
ребро.
(2)
і (3) ![]() (1). Хай в графові, що не має циклів,
(1). Хай в графові, що не має циклів, ![]() ребро,
а його компонентами зв'язності є
ребро,
а його компонентами зв'язності є ![]() ,
причому
,
причому ![]() складається з
складається з ![]() вершин,
вершин, ![]() .
Кожна компонента є деревом, тому, як
доведено вищим, число ребер в
.
Кожна компонента є деревом, тому, як
доведено вищим, число ребер в ![]() рівне
рівне ![]() ,
а всього ребер в графі
,
а всього ребер в графі ![]() .
Значить, і граф зв'язний.
.
Значить, і граф зв'язний.
(1)
і (3) ![]() (2). Розглянемо зв'язний граф з
(2). Розглянемо зв'язний граф з ![]() ребром. Якби в ньому був цикл, то, видаливши
будь-яке циклове ребро, ми отримали б
зв'язний граф з меншим числом ребер.
Можна продовжувати таке видалення ребер
до тих пір, поки не залишиться зв'язний
граф без циклів, тобто дерево. Але ребер
в цьому дереві було б менше, ніж
ребром. Якби в ньому був цикл, то, видаливши
будь-яке циклове ребро, ми отримали б
зв'язний граф з меншим числом ребер.
Можна продовжувати таке видалення ребер
до тих пір, поки не залишиться зв'язний
граф без циклів, тобто дерево. Але ребер
в цьому дереві було б менше, ніж ![]() ,
а це протирічить доведеному вище.
,
а це протирічить доведеному вище.
Теорема
2. Якщо ![]() – дерево, то
– дерево, то
у
 будь-яка пара вершин сполучена єдиним
шляхом;
будь-яка пара вершин сполучена єдиним
шляхом; при додаванні до
 будь-якого нового ребра утворюється
цикл;
будь-якого нового ребра утворюється
цикл; при видаленні з
 будь-якого ребра він перетворюється
на незв'язний граф.
будь-якого ребра він перетворюється
на незв'язний граф.
Доведення.
Існування
шляху між будь-якими двома вершинами
виходить із зв'язності дерева. Допустимо,
що в деякому дереві існують два різні
шляхи, що сполучають вершини
![]() і
і![]() .
Початкові відрізки цих шляхів збігаються
(обидва шляхи починаються в одній і тій
же вершині
.
Початкові відрізки цих шляхів збігаються
(обидва шляхи починаються в одній і тій
же вершині![]() ).
Хай
).
Хай![]() – остання вершина цього співпадаючого
початку, а після
– остання вершина цього співпадаючого
початку, а після ![]() в одному шляху слідує вершина
в одному шляху слідує вершина ![]() ,
а в іншому – вершина
,
а в іншому – вершина ![]() .
Розглянемо ребро
.
Розглянемо ребро ![]() .
Якщо його видалити з графа, то в тому,
що залишився, підграфові вершини,
.
Якщо його видалити з графа, то в тому,
що залишився, підграфові вершини, ![]() і
і
![]() будуть з’єднаними – маршрут, що сполучає
їх, можна побудувати так: взяти відрізок
першого шляху від
будуть з’єднаними – маршрут, що сполучає
їх, можна побудувати так: взяти відрізок
першого шляху від ![]() до
до
![]() і до нього приєднати відрізок другого
від
і до нього приєднати відрізок другого
від![]() до
до
![]() ,
узятий в зворотному порядку. Але це
означає, що ребро
,
узятий в зворотному порядку. Але це
означає, що ребро![]() не є перешийком. Проте з теореми 4 лекції
3 витікає, що в дереві кожне ребро є
перешийком. Цим доведено твердження
1). Твердження 2) і 3) виходять з 1).
не є перешийком. Проте з теореми 4 лекції
3 витікає, що в дереві кожне ребро є
перешийком. Цим доведено твердження
1). Твердження 2) і 3) виходять з 1).
Відзначимо, що єдиний шлях, що сполучає дві вершини дерева, завжди простий (якщо шлях не є простим, в ньому обов'язково міститься цикл).
