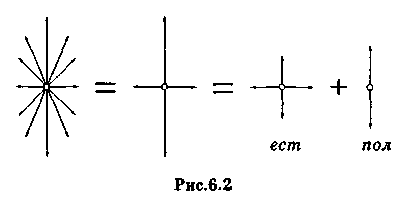Поляризация
Виды
поляризации. Волну,
в которой направление колебаний
светового вектора
![]() упорядочено каким-либо образом, называют
поляризованной.
Если
колебания вектора
упорядочено каким-либо образом, называют
поляризованной.
Если
колебания вектора
![]() происходят только
в одной плоскости, проходящей через
луч, то мы имеем дело
с плоско-
(или
линейно-)
поляризованной волной.
Плоскость,
в которой колеблется вектор
происходят только
в одной плоскости, проходящей через
луч, то мы имеем дело
с плоско-
(или
линейно-)
поляризованной волной.
Плоскость,
в которой колеблется вектор
![]() ,
называют плоскостью
поляризации
(плоскостью колебаний светового вектора).
Первоначально плоскость поляризации
связывали с плоскостью, в которой
колеблется
вектор Н
или В.
Несмотря на то, что это устарело в
некоторых учебниках до сих пор понятие
«плоскость
поляризации» используется в прежнем
смысле.
,
называют плоскостью
поляризации
(плоскостью колебаний светового вектора).
Первоначально плоскость поляризации
связывали с плоскостью, в которой
колеблется
вектор Н
или В.
Несмотря на то, что это устарело в
некоторых учебниках до сих пор понятие
«плоскость
поляризации» используется в прежнем
смысле.
Другой
вид поляризации заключается в том, что
вектор
![]() вращается вокруг направления
распространения волны одновременно
изменяясь периодически по модулю. При
этом конец вектора
Е описывает эллипс (в каждой точке
среды). Такую волну
называют эллиптически-поляризованной.
Или
поляризованной
по кругу,
если
конец вектора
вращается вокруг направления
распространения волны одновременно
изменяясь периодически по модулю. При
этом конец вектора
Е описывает эллипс (в каждой точке
среды). Такую волну
называют эллиптически-поляризованной.
Или
поляризованной
по кругу,
если
конец вектора
![]() описывает окружность.
описывает окружность.
В
зависимости от направления вектора
![]() различают правую
и
левую
эллиптические
(или круговые) поляризации. Если смотреть
навстречу
распространения
волны, и вектор
различают правую
и
левую
эллиптические
(или круговые) поляризации. Если смотреть
навстречу
распространения
волны, и вектор
![]() при этом
поворачивается по
часовой
стрелке, то поляризацию называют
правой,
в
противном случае (если против
часовой
стрелки)
— левой.
при этом
поворачивается по
часовой
стрелке, то поляризацию называют
правой,
в
противном случае (если против
часовой
стрелки)
— левой.
Эллиптически-поляризованная — это наиболее общий вид поляризации волны.
|
|
Несмотря на то, что световые волны и от обычных источников поперечны, они, как правило, не обнаруживают асимметрии по отношению к направлению распространения. Такой свет называют естественным. |
|
Рисунок 18 |
Естественный свет можно представить как наложение (сумму) двух некогерентных плоско поляризованных волн с взаимно ортогональными плоскостями поляризации, что и показано на рис. 18 справа.
Поляризаторы. Из естественного света можно получить плос-кополяризованный с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания светового вектора, параллельные плоскости, которую мы будем называть плоскостью пропускания поляризатора. Колебания же, перпендикулярные к этой плоскости, задерживаются полностью или частично.
Разложим
![]() на компоненты:
на компоненты:![]() и пусть
и пусть![]() .
.
Тогда

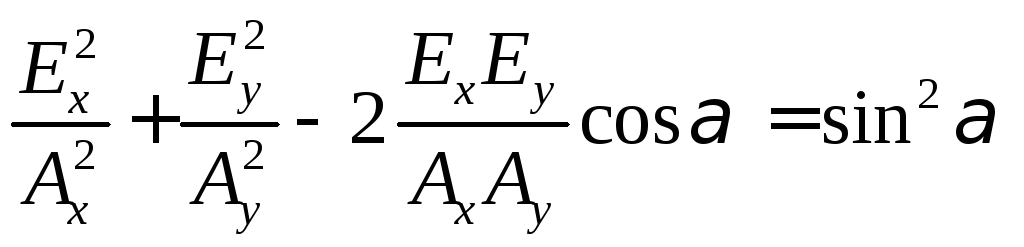 –уравнение
траектории конца
–уравнение
траектории конца
![]() .
.
При
![]() будет
будет – линейная поляризация.
– линейная поляризация.
При
![]() будет
будет – эллиптическая поляризация. Если
вдобавок
– эллиптическая поляризация. Если
вдобавок![]() ,
то поляризация круговая.
,
то поляризация круговая.
Поляризатор
пропускает все волны, вектор
![]() в которых колеблется в определённом
направлении (например,
в которых колеблется в определённом
направлении (например,![]() ).
Тогда, если
).
Тогда, если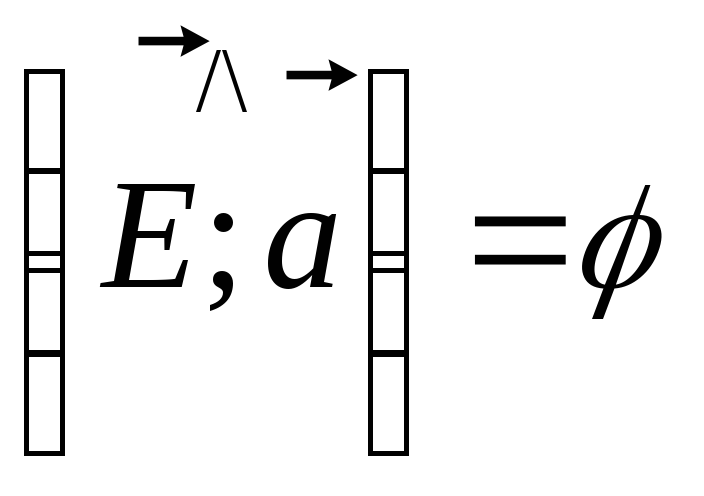 ,
то
,
то![]() и, т.к.
и, т.к.![]() .
.
![]() – закон
Малюса.
– закон
Малюса.
Степень поляризации. Помимо плоскополяризованного и естественного света существует еще «промежуточный» случай — частично-поляризованный свет. Его можно рассматривать как сумму естественной (ест) и плоскополяризованной (пол) составляющих, как показано на этом рисунке 19 справа.
|
|
Частично поляризованный свет характеризуют степенью поляризации Р, которую определяют как
|
|
Рисунок 19 |
.
Здесь
![]() и
и![]() — максимальная и минимальная интенсивность
перпендикулярных составляющих световой
волны;
— максимальная и минимальная интенсивность
перпендикулярных составляющих световой
волны;![]() -
интенсивность поляризованной составляющей,
-
интенсивность поляризованной составляющей,![]() —
суммарная интенсивность
неполяризованной и поляризованной
составляющих.
—
суммарная интенсивность
неполяризованной и поляризованной
составляющих.
О деполяризации. Иногда возникает обратная задача: поляризованный свет превратить в естественный, т. е. неполяризованный. Это можно достигнуть пропуская поляризованный свет через слой мелко истолченного стекла или кальку.
. Поляризация при отражении и преломлении
Закон Брюстера. Если угол падения естественного света на границу раздела двух прозрачных диэлектриков отличен от нуля, то отражен ный и преломленный пучки оказываются частичнополяризованными.
|
|
В
отраженном свете преобладают колебания
вектора
|
|
Рисунок 20 |
Этот
угол
![]() удовлетворяет
следующему
условию:
удовлетворяет
следующему
условию:
![]() ,
,
Данное
соотношение называют
законом
Брюстера,
а
угол
![]() —
углом
Брюстера или
углом
полной
поляризации.
Здесь
п2
/п1
—
отношение
показателей преломления второй
среды и первой (рис. 20).
—
углом
Брюстера или
углом
полной
поляризации.
Здесь
п2
/п1
—
отношение
показателей преломления второй
среды и первой (рис. 20).
Можно убедиться, что при падении света под углом Брюстера отраженный и преломленный лучи взаимно ортогональны.
Формулы Френеля:
Без вывода. Из граничных условий для напряженностей полей на границе раздела двух сред получаем
 ;
;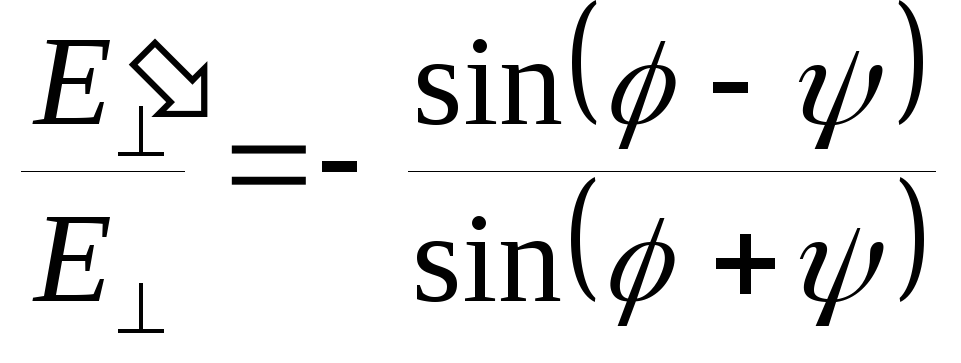 ;
;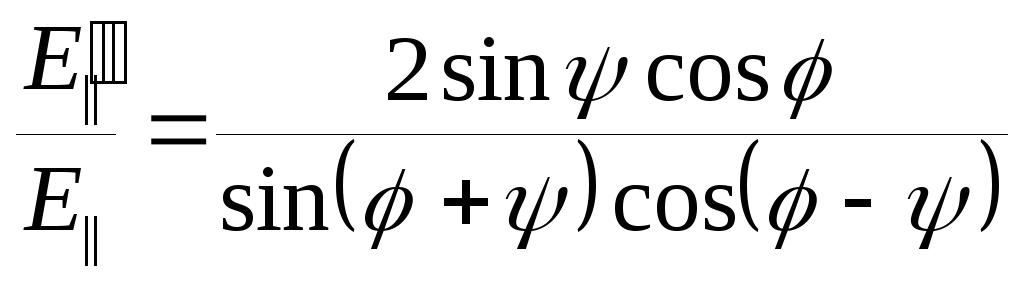 ;
; .
.
Соотношение интенсивностей можно получить отсюда возведя правые части в квадрат.
Рассмотрим случай
почти нормального падения, т.е. когда
и
– очень малые углы. Тогда
![]() и формулы преобразуются следующим
образом:
и формулы преобразуются следующим
образом:
 ;
; ;
; ;
; .
.
Коэффициент отражения
 .
.
Коэффициент прохождения
 .
.