Колебательный контур

Здесь будем предполагать, что в рас­сматриваемых случаях условие квазистационарности (мгновенные значения тока оказываются практически одинаковыми на всех участках цепи) выполненным. Это позволит использовать формулы, по­лученные для статических полей

В цепи, содержащей катушку индуктивности и конденсатор емкости, могут возник­нуть электрические колебания. Поэтому такую цепь назы­ваютколебательным контуром. Выясним, каким образом в колебательном контуре возникают и под­держиваются электрические колебания.

Пусть вначале верхняя обкладка конденсатора заря­жена положительно, а нижняя отрицательно (рис. 26.8.). При этом вся энергия контура со­средоточена в конденсаторе. Замкнем ключ. Конденса­торначнет разряжаться, и через катушкупотечет ток. Электрическая энергия конденсатора начнет превращать­ся в магнитную энергию катушки. Этот процесс закончит­ся, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума. С этого момента ток, не меняя направления, начнет убывать. Однако он прекра­тится не сразу — его будет поддерживать э. д. с. самоин­дукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет макси­мума. С этого момента конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т. д.— про­цесс будет повторяться.

Уравнение колебательного контура.

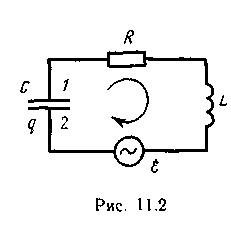
	Найдем уравнение колебаний в контуре, содержащем последова­тельно соеди­ненные конденсатор , катушку индуктивности, активное сопротивлениеи внешнюю переменную э. д. с.(см.Рисунок 26.8.). Прежде всего выберем положительное направление об­хода контура, например по часовой стрелке. Обозначим череззаряд той обкладки конденсатора, направление от которой к другой обкладке (внутри конденсатора)
Рисунок 26.8.

совпадает с выбранным по­ложительным направлением обхода контура. Тогда ток в контуре определяется как

(26.32)

Согласно закону Ома для участка цепи

,

(26.33)

где — э. д. с. самоиндукции. В нашем случае

и

(26.34)

Поэтому уравнение (26.33) можно переписать в виде

.

(26.35)

Это и есть уравнение колебательного контура — линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициен­тами.

вВ случае, когда внешняя э. д. с. отсутствует, в контуре при отсутствии сопротивления проводников будут совершаться строго периодические колебания; если же сопротивление проводников, то помимо описанного процесса будет происходить преобразование электромагнитной энергии в джоулеву теплоту.

Установившиеся колебания. Рассмотрим случай, когда контур состоит из конденсатора, индуктивности, сопротивления и внешней переменной ЭДС:

.

(26.36)

Этот закон занимает особое положение благодаря свойству самого колебательного контура сохранять гармонический вид колебаний при действии внешней гармонической ЭДС.

Закон Ома для такого колебательного контура примет вид:

.

(26.37)

Решение этого уравнения есть

,

(26.38)

где первый член является общим решением однородного уравнения без правой части, а второй частное решение неоднородного уравнения. Причём величины иопределяются начальными условиями,, аиравны:

(26.39)

Эти формулы взяты из курса колебаний 2 семестра. Подставим в них значения и

,

(26.40)

получим выражения:

(26.41)

(26.42)

Выражение под корнем

(26.43)

называют полным сопротивление илиимпедансом, выражение в скобках называютреактивным сопротивлением,

,

(26.44)

выражение

(26.45)

называют емкостным сопротивлением, выражение

,

(26.46)

называют индуктивным сопротивлением, а величину–активным сопротивлением.

В уравнении (26.38) первое слагаемое экспоненциально затухает и по прошествии достаточного времени им можно пренебречь. При больших временых главный вклад в решение дает второе слагаемое. Такое решение называется установившимися колебаниями.

Далее рассматрим именно их:

.

(26.47)

Фазовые соотношения. Продифференцировав выражение (26.47) по времени найдём силу тока при установившихся колебаниях:

,

(26.48)

где сдвиг фаз между током и приложенной к контуру ЭДС.

В соответствии с формулой приведения

(26.49)

Из этой формулы следует, что при ток отстаёт по фазе от ЭДС, а приопережает.

Амплитуда тока равна

.

(26.50)

Напряжение на сопротивлении равно

.

(26.51)

Напряжение на конденсаторе равно

.

(26.52)

Напряжение на индуктивности

.

(26.53)

Сумма на отдельных элементах контура равна в каждый момент времени приложенной к контуру эдс:

.

(26.54)

Фазовые соотношения можно наглядно представить с помощью векторной диаграммы. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (см. Рис. 26.9)

Рисунок 26.9.

Заметим, что из прямоугольного треугольника на диаграмме легко можно получить формулу (26.50). Так же на ней хорошо видны фазовые отношения. Так напряжение на активном сопротивлении совпадает по фазе с током. Напряжение на емкости отстает по фазе на , а напряжение на индуктивности наоборот опережает наток.

Резонансные кривые.Резонансная частота для заряда и напряжения на конденсаторе равна

,

(26.55)

и получается нахождением минимума подкоренного выражения в формуле ().

Резонансные кривые изобра­ены на рис. 26.10. Они сходны с резонансными кривыми для q. Максимум при резонансе получается тем выше, чем меньше коэффициент затухания, т.е. чем меньше активное сопротивление и больше индуктивность. Резонансные кривые для тока даны на рис.26.11. Как видно из выражения (26.50) максимум амплитуды тока достигается при . Следовательно, резонансная частота совпадает с собственной частотой контура: (26.56)

Рисунок 26.10.

	Резонансные частоты для тока и напряжения на сопротивлении совпадают, так как UR=IR.. Резонансная частота для ULопределяется дифференци­ированием функции Результат таков (26.57)
Рисунок 26.11.

Приведём график, на котором вместе изобразим резонансные кривые для

	напряжений на сопро­тивлении, конденсаторе и индуктивности, рис. 26.12. Чем меньше коэффициент затухания, тем ближе резонансные частоты всех величин к одному и тому же значению равному ω0.
Рисунок 26.12.

.

Резонансные кривые и добротность. Форма резонансных кривых определённым образом связана с добротностью контура. Особенно простой эта связь оказывается приβ<<ω₀. В этом случае с одной стороны

(26.58)

а с другой стороны

(26.59)

Следовательно, добротность контура (при малом затухании) показывает, во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней ЭДС:

(26.60)

Добротность контура связана с другой важной характеристикой резонансной кривой – ее шириной. Оказывается при малом затухании

(26.61)

где δω– ширина резонансной кривой на «высоте», равной 0,7 от максимальной, т.е. в резонансе.

18