
- •Лекция 29.
- •Скорость эмв в среде
- •Плоская электромагнитная волна
- •Импульс электромагнитной волны
- •Экспериментальное получение электромагнитных волн. Вибратор Герца.
- •Излучение диполя
- •Отражение и преломление плоской волны на границе двух диэлектриков
- •Коэффициент отражения и коэффициент пропускания плоской электромагнитной волны
- •Шкала электромагнитных волн
Отражение и преломление плоской волны на границе двух диэлектриков
Опыт показывает, что при падении на диэлектрик электромагнитной волны возникает как отраженная, так и преломлённая волна.
Определим направление
распространения падающей волны с помощью
вектора
![]() ,
преломлённой с помощью вектора
,
преломлённой с помощью вектора![]() 2,
отражённой с помощью вектора
2,
отражённой с помощью вектора
![]() 3
(см. рис.
29.5). Найдём их связь друг с другом. Это
можно сделать, воспользовавшись условием
3
(см. рис.
29.5). Найдём их связь друг с другом. Это
можно сделать, воспользовавшись условием
![]() .
.
Результирующее поле в первой среде будет суперпозицией падающей и отраженной волн (запишем их в комплексном виде и знак Re опустим):
|
|
(29.27) |
Д ля
того, что бы условие выполнялось для
всех t,
необходимо равенство
ля
того, что бы условие выполнялось для
всех t,
необходимо равенство
|
|
частот
Для того, что бы
условие (29.27) выполнялось при любом х,
необходимо равенство тангенциальных
проекций волновых векторов (на ось
х):
|
|
Рисунок 29. 5 |
Из рисунка 29.5 видно, что
|
|
(29.28) |
или
|
|
(29.29) |
так как
![]() ,
то
,
то![]() – угол падения равен углу отражения
волны. Также отсюда вытекает, что
– угол падения равен углу отражения
волны. Также отсюда вытекает, что
|
|
(29.30) |
Это выражение
является законом
преломления.
Величина
![]() называется
относительным
показателем преломления.
Представим эту величину в виде:
называется
относительным
показателем преломления.
Представим эту величину в виде:
|
|
(29.31) |
И, следовательно
|
|
(29.32) |
Из этой формулы видно, что при переходе луча из оптически более плотной среды в оптически менее плотную преломлённый луч ложится на поверхность раздела, и наступает «полное внутреннее отражение», когда весь падающий луч полностью отражается от границы раздела сред. Угол, определяемый формулой
|
|
(29.33) |
называется предельным углом.
При углах падения
от
![]() θпред
до
θпред
до
![]() ,
световая волна проникает во вторую
среду на расстояние порядка длины волны
и затем возвращается в первую среду.
,
световая волна проникает во вторую
среду на расстояние порядка длины волны
и затем возвращается в первую среду.
Рассмотрим, что происходит с амплитудами и фазами при прохождении волны через границу раздела сред.
|
|
Для простоты ограничимся случаем нормального падения волны (См. Рис.29.6).
Модули
|
|
Рисунок 29.6. |
Напишем условия
непрерывности тангенциальных составляющих
векторов
![]() и
и
![]() :
:
|
|
(29.34) |
Так как
![]() ,
а в отраженной волне вектора
,
а в отраженной волне вектора
![]() и
и
![]() имеют разные знаки, то уравнения (29.)
можно записать:
имеют разные знаки, то уравнения (29.)
можно записать:
|
|
(29.35) |
Решив эти уравнения совместно, получим значения для Е и запишем их в векторном виде
|
|
(29.36) |
Отсюда следует, что:
Вектор
 всегда сонаправлен с вектором
всегда сонаправлен с вектором
 –
при прохождении через границу раздела
фаза не претерпевает скачка.
–
при прохождении через границу раздела
фаза не претерпевает скачка.Это же относится к векторам
 и
и
 ,
но при условии, что
,
но при условии, что
 ,
в противном
случае (когда
,
в противном
случае (когда
 )
дробь в выражении становится отрицательной,
а это значит, что направление вектора
)
дробь в выражении становится отрицательной,
а это значит, что направление вектора
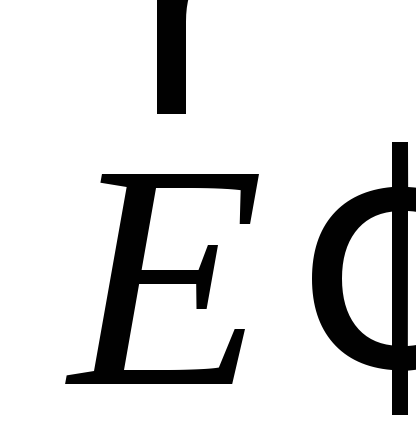 противоположно направлению вектора
противоположно направлению вектора
 .
При
отражении волны от оптически более
плотной среды её фаза изменяется скачком
на
.
При
отражении волны от оптически более
плотной среды её фаза изменяется скачком
на
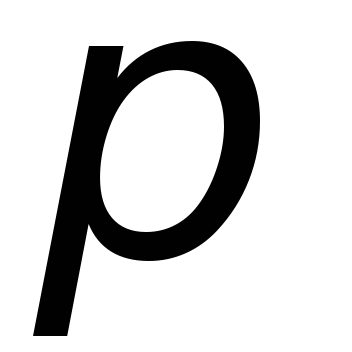 .
.



 .
.