Федун В.И. Конспект лекций по физике Электромагнетизи

Лекция 29.

29	Скорость и энергия ЭМВ. Вектор Пойнтинга. Излучение ЭМВ. Отражение и преломление ЭМВ. Шкала электромагнитных волн.

Скорость эмв в среде

Получено два волновых уравнения:

,.

(29.1)

Если = 1 и= 1 ( в вакууме), то коэффициентв уравнении есть величина связанная со скоростью распространения электромагнитной волны:

.

(29.2)

Тогда скорость в среде равна

(29.3)

Теперь уравнения (29.1) принимают вид

.

(29.4)

Плоская электромагнитная волна

Направим ось перпендикулярно волновым поверхностям плоской волны. При этомине будут зависеть оти, и соответствующие производные будут равны нулю. Тогда уравнения Максвелла:

,
,	(29.5)
,.

примут вид:

.

(29.6)

Отсюда следует, что Е_х и Н_х не зависят ни от х, ни от t. Это значит, что отличные от нуля Е_х и Н_х могут быть только однородными постоянными полями, накладывающимися на поле волны. В самой волне они равны нулю. Это значит, что электромагнитная волна является поперечной.

Кроме того, векторы ив электромагнитной волне взаимно ортогональны. Возьмём пару уравнений (29.6):

.

(29.6а)

Из них видно, что изменение во времени магнитного поля, направленного вдоль оси , порождает электрическое полеЕ_у вдоль оси . И наоборот. Ни поляЕ_z , ни поля Н_у при этом не появляется, а это и значит, что .

Связь мгновенных значений и

Когда плоская волна распространяется вдоль положительного направления оси , то в общем случае можно записать

.

(29.7)

Введя обозначение , найдём производные:

.

(29.8)

Подставив эти выражения в уравнение , получим

.

(29.9)

Проинтегрировав, получим

,

(29.10)

где константа обусловлена наличием постоянного электрического и магнитного полей. Нас интересует только переменное поле, поэтому константу положим равной нулю:

.		(29.11)
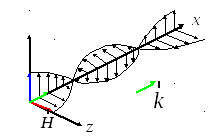
Рисунок 29. 1

Замечания.

Выражение (29.11) означает:

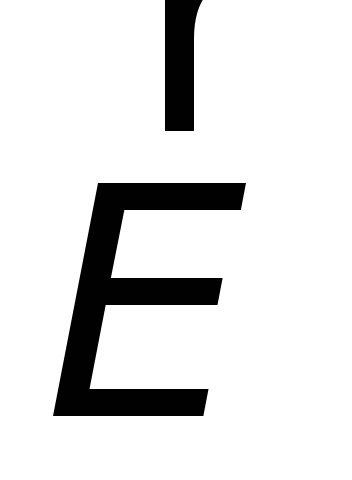1. и 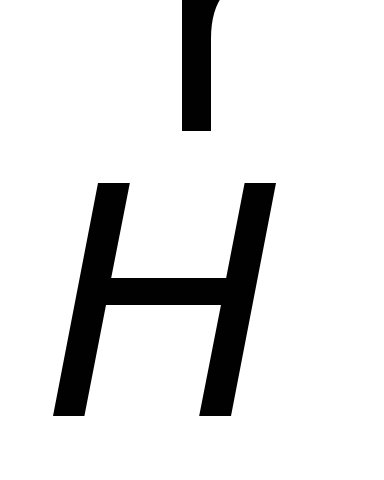взаимно ортогональны.

2. Они составляют правовинтовую систему с направлением распространения.

3. Изменяются синфазно - одновременно достигают максимума и одновременно обращаются в нуль.

4. Уравнение плоской гармонической электромагнитной волны будет иметь вид:

   .

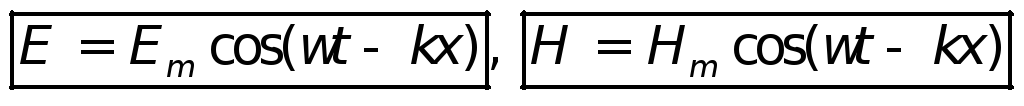   (29.12)

5. Если бы волна распространялась в отрицательном направлении, то 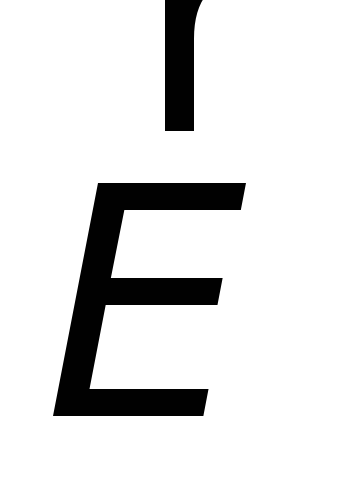и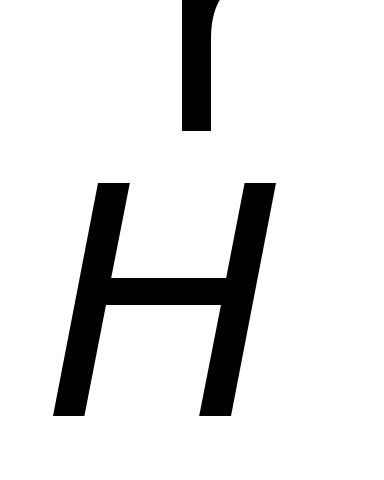изменялись бы в противофазе:

,

хотя сами вектора и составляли бы по-прежнему правовинтовую систему.

Энергия и плотность потока энергии электромагнитной волны

В обычной изотропной среде плотность энергии электромагнитного поля равна сумме плотностей энергий:

.

(29.12)

Умножив на скорость волны, получим плотность потока энергии:

.

(29.13)

Векторы ивзаимно ортогональны. Направление векторасовпадает с направлением переноса энергии, поэтому можно определить вектор плотности потока энергии так

.

(29.13)

Вектор плотности потока энергии называют вектором Пойнтинга.

Интенсивность бегущей волны равна, по определению, среднему значению плотности потока энергии:

.

(29.14)

I пропорционально квадрату амплитуды .
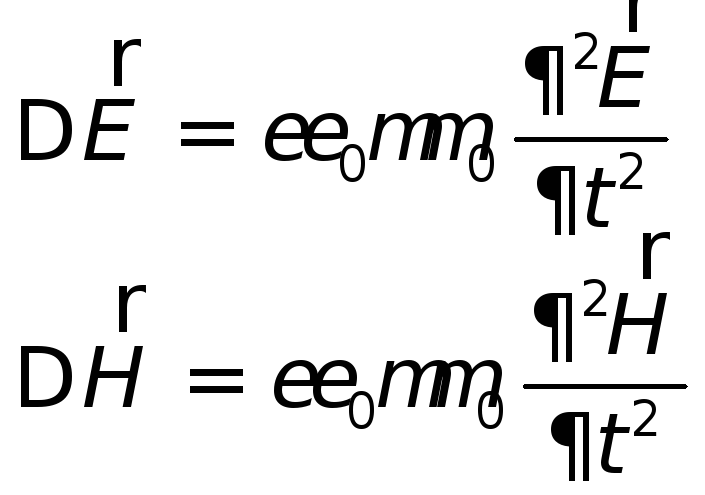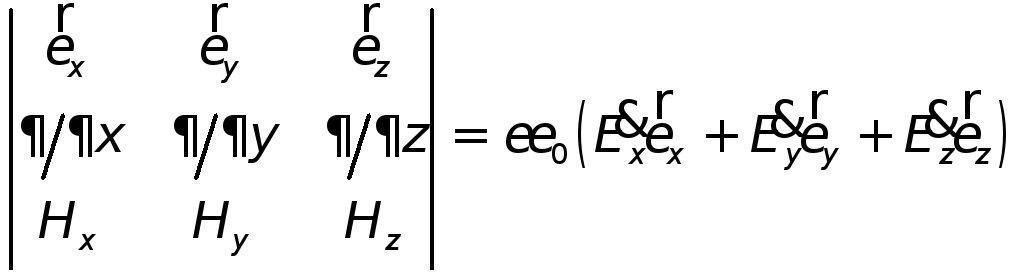
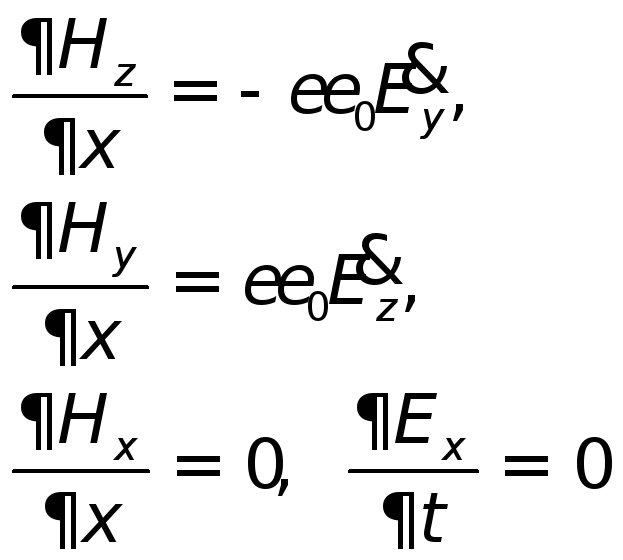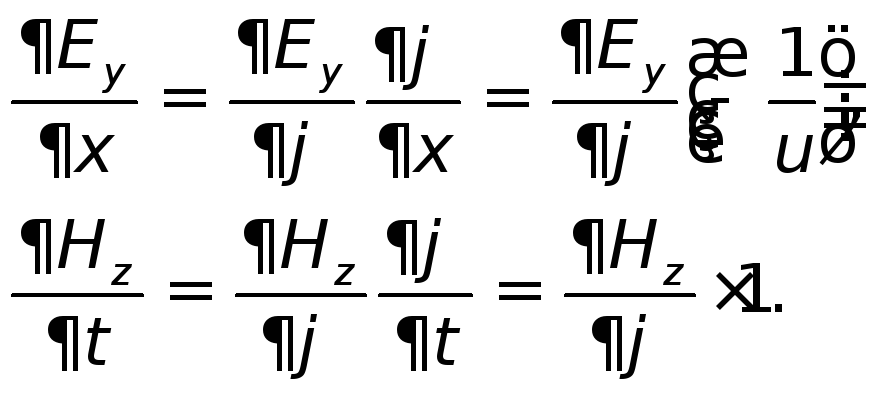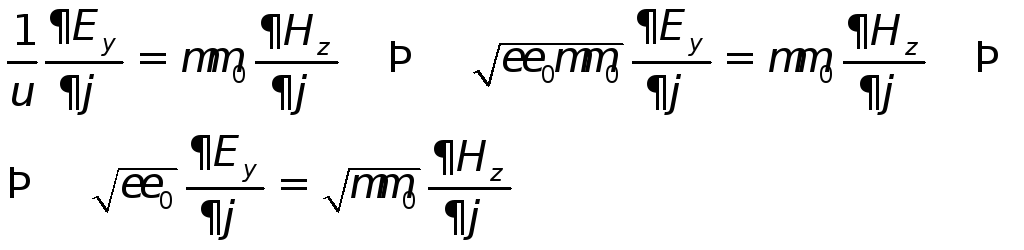
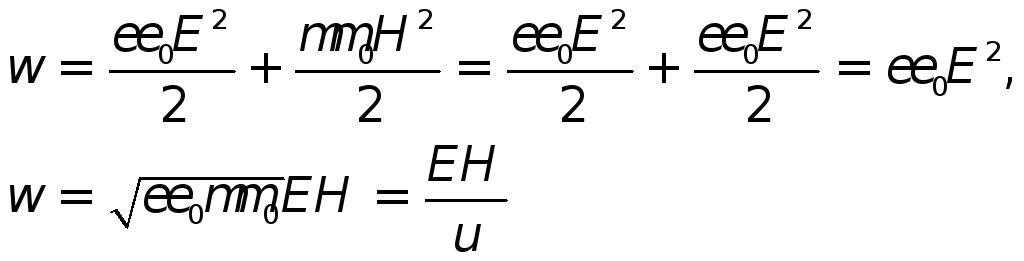