
Соотношение неопределенностей Гейзенберга3
Наличие противоречий при рассмотрении движения микрочастиц потребовало фундаментального изменения в основных классических представлениях и законах. Наличие волновых свойств у частиц должно накладывать определенные ограничения на применимость по отношению к ним понятий классической физики: импульс, координата, траектория. В пользу этого утверждения можно привести следующие аргументы:
В соответствии с гипотезой Де Бройля импульс зависит только от длины волны
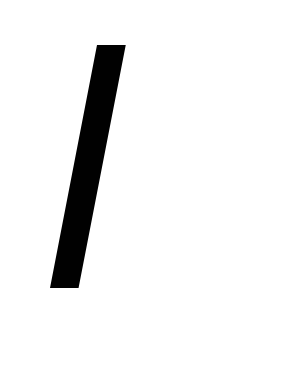 :
:
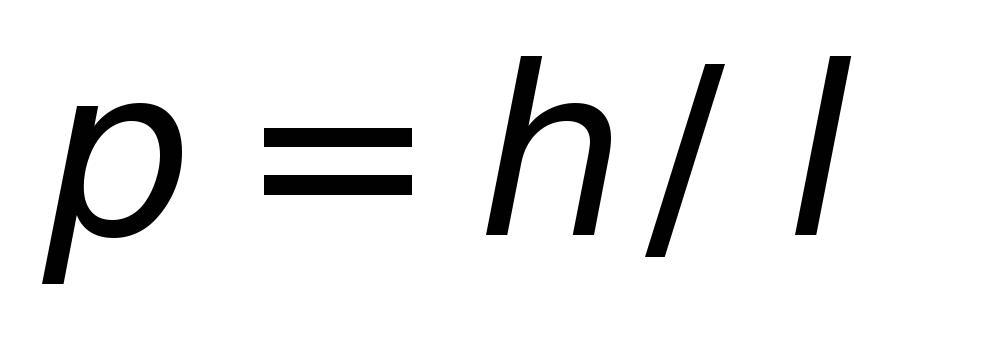 ,
а в классическом случае
,
а в классическом случае
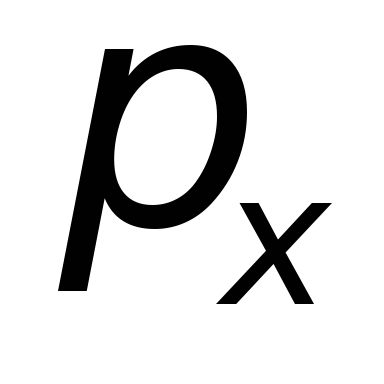 должно зависеть от
должно зависеть от (фазовая траектория).
(фазовая траектория).И
 з
предыдущей лекции известно, что ширина
волнового пакета
з
предыдущей лекции известно, что ширина
волнового пакета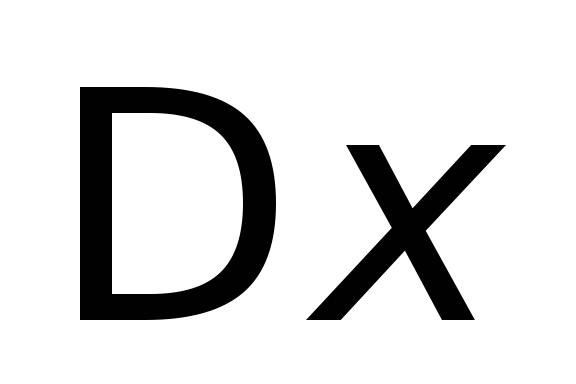 и интервал волновых чисел
и интервал волновых чисел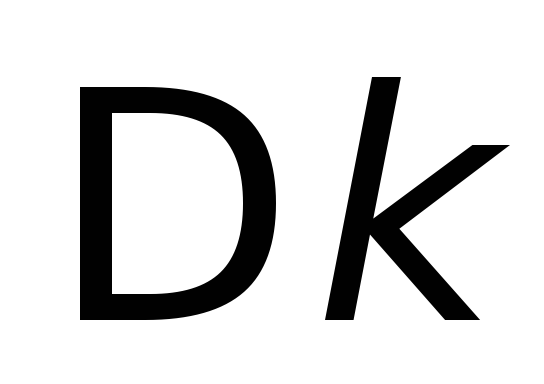 требуемых
для его представления в виде суперпозиции
гармонических волн связаны соотношением:
требуемых
для его представления в виде суперпозиции
гармонических волн связаны соотношением: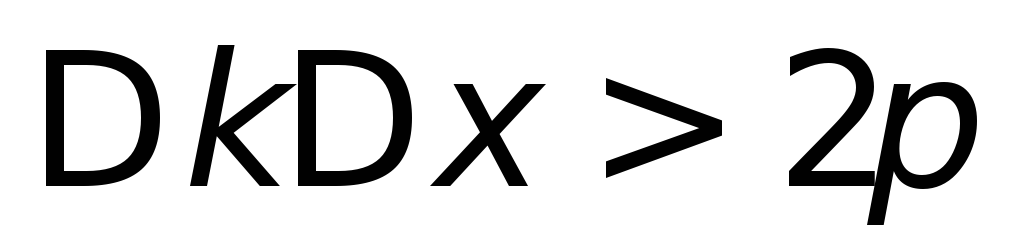 .
Умножив левую и правую часть на
.
Умножив левую и правую часть на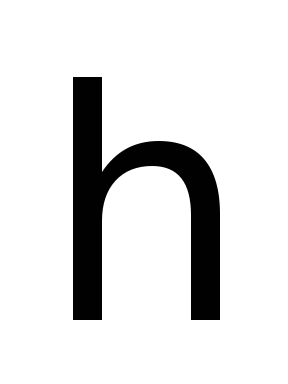 и воспользовавшись гипотезой Де Бройля
получим:
и воспользовавшись гипотезой Де Бройля
получим:
![]()
Здесь
под
![]() будем подразумевать область пространства,
в котором локализована частица,
будем подразумевать область пространства,
в котором локализована частица,![]() —разброс
значений (погрешность) импульса частицы.
—разброс
значений (погрешность) импульса частицы.
Оценим неточность (погрешность) при определении координаты и импульса частицы при прохождении через щель ширины
 (Рис.2.1).
(Рис.2.1). Будем полагать, что слева на щель падает
моноэнергетический пучок электронов
с импульсом
Будем полагать, что слева на щель падает
моноэнергетический пучок электронов
с импульсом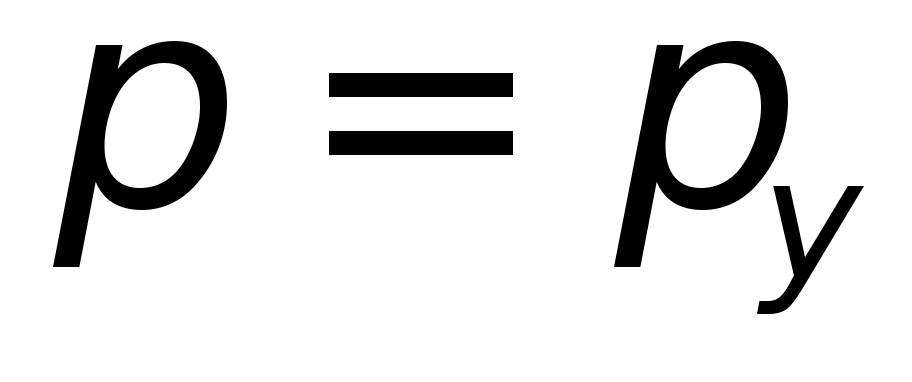 (
(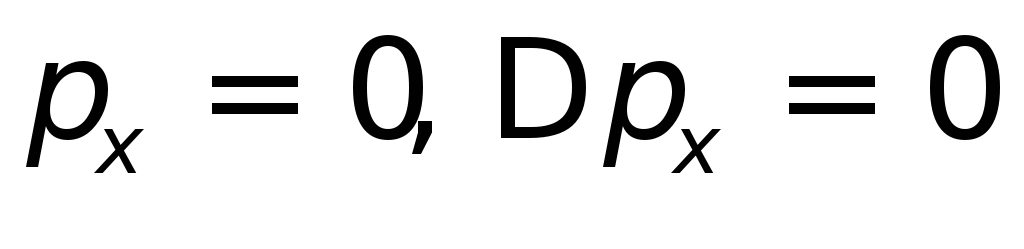 ,
, —
— координата
является совершенно неопределенной).
В момент прохождения щели координата
частиц вдоль оси
координата
является совершенно неопределенной).
В момент прохождения щели координата
частиц вдоль оси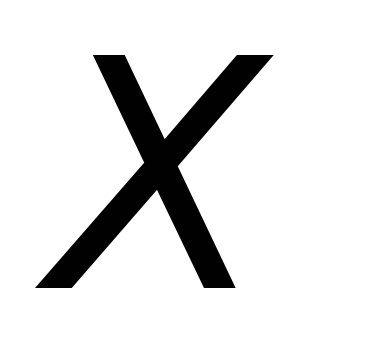 известна с ошибкой
известна с ошибкой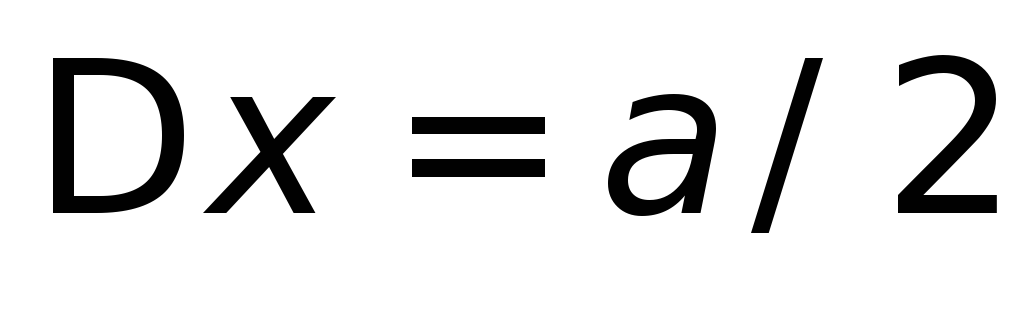 ,
что достигается ценой утраты определенности
,
что достигается ценой утраты определенности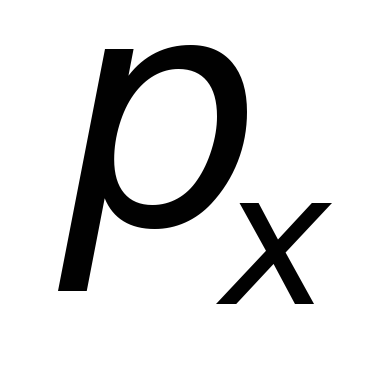 .
Действительно, при наличии волновых
свойств у электронов, на экране будет
наблюдаться система дифракционных
полос (в отличие от одной полосы ширины
.
Действительно, при наличии волновых
свойств у электронов, на экране будет
наблюдаться система дифракционных
полос (в отличие от одной полосы ширины в классическом случае). Направления на
дифракционные минимумы определяются
по формуле
в классическом случае). Направления на
дифракционные минимумы определяются
по формуле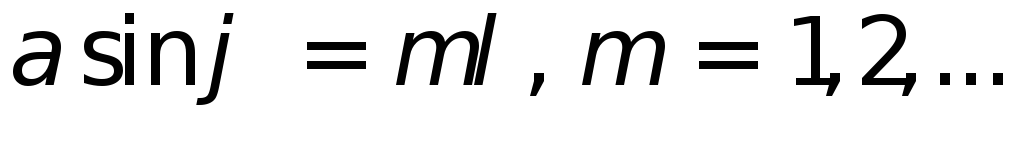 .
Таким образом, размер изображения щели
на экране (определяемый направлением
на первый дифракционный минимум
.
Таким образом, размер изображения щели
на экране (определяемый направлением
на первый дифракционный минимум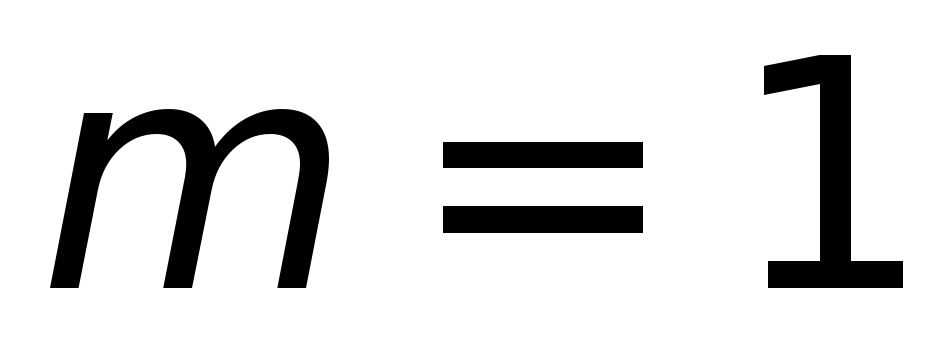 )
будет больше ширины щели, что возможно
в случае, если частицы после щели имеют
компоненту импульса вдоль
)
будет больше ширины щели, что возможно
в случае, если частицы после щели имеют
компоненту импульса вдоль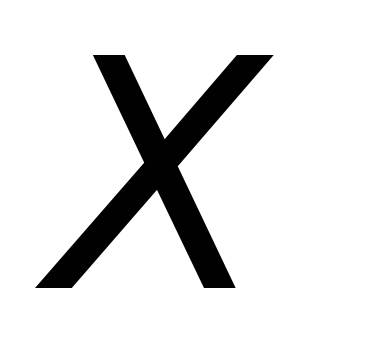 .
Обозначим
.
Обозначим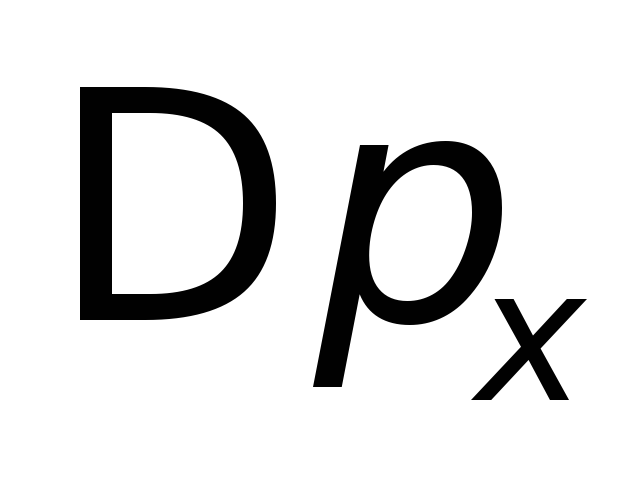 максимальное значение компоненты
импульса при движении электрона в
направлении первого дифракционного
минимума. По физическому смыслу
максимальное значение компоненты
импульса при движении электрона в
направлении первого дифракционного
минимума. По физическому смыслу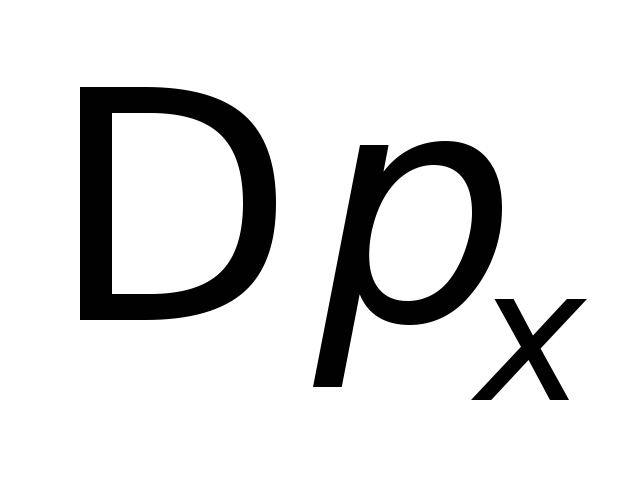 определяет погрешность в определении
определяет погрешность в определении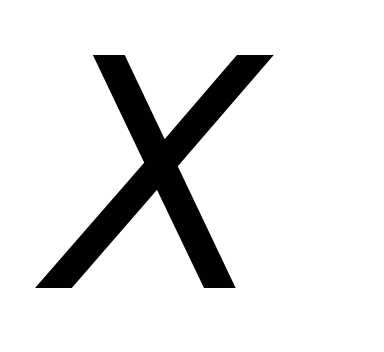 -компоненты
импульса после прохождения частиц
через щель. Тогда получим:
-компоненты
импульса после прохождения частиц
через щель. Тогда получим:
![]()
![]()
![]()
![]()
![]()
Таким
образом, видно, что попытка точно
определить координату
![]() приводит к появлению дополнительного
импульса вдоль оси
приводит к появлению дополнительного
импульса вдоль оси![]() .
В данном случае также понятно, что
.
В данном случае также понятно, что![]() координата
частицы оказывается неопределенной,
зато
координата
частицы оказывается неопределенной,
зато![]() известна
точно. При измерении координаты квантового
объекта мы неизбежно сбиваем его с
курса, теряя при этом информацию о
направлении его движения и фазе.
известна
точно. При измерении координаты квантового
объекта мы неизбежно сбиваем его с
курса, теряя при этом информацию о
направлении его движения и фазе.
Вывод:
произведение погрешностей в определении
координат и соответствующих импульсов
![]() .
Это означает, что при уменьшении
погрешности (увеличении точности
измерений) в определении координаты
.
Это означает, что при уменьшении
погрешности (увеличении точности
измерений) в определении координаты![]() мы
увеличиваем погрешность при определении
импульса
мы
увеличиваем погрешность при определении
импульса![]() .
Таким образом, процесс воздействия
измерения на исследуемый объект (в
отличие от классической физики) нельзя
сделать сколь угодно малым: чем точнее
измерение тем сильнее его воздействие.
С точки зрения квантовой механики,
процесс измерения заключается в
следующем: физический прибор, подчиняющейся
законам классической физики, взаимодействует
с квантово-механическим объектом. До
взаимодействия прибор и объект находятся
в своих состояниях, которые в результате
взаимодействия изменяются. По характеру
и величине изменения состояния прибора
(которые определяются по его показаниям)
можно судить о состоянии объекта до
взаимодействия. Нетрудно видеть, что
изменение состояния объекта в процессе
измерения приводит к невоспроизводимости
результатов эксперимента: если мы при
первом измерении величины
.
Таким образом, процесс воздействия
измерения на исследуемый объект (в
отличие от классической физики) нельзя
сделать сколь угодно малым: чем точнее
измерение тем сильнее его воздействие.
С точки зрения квантовой механики,
процесс измерения заключается в
следующем: физический прибор, подчиняющейся
законам классической физики, взаимодействует
с квантово-механическим объектом. До
взаимодействия прибор и объект находятся
в своих состояниях, которые в результате
взаимодействия изменяются. По характеру
и величине изменения состояния прибора
(которые определяются по его показаниям)
можно судить о состоянии объекта до
взаимодействия. Нетрудно видеть, что
изменение состояния объекта в процессе
измерения приводит к невоспроизводимости
результатов эксперимента: если мы при
первом измерении величины![]() определили
что она равна
определили
что она равна![]() ,
и сразу же после этого, произвели ее
повторное измерение, то полученное
значение
,
и сразу же после этого, произвели ее
повторное измерение, то полученное
значение![]() ,
уже не будет совпадать с результатом
первого эксперимента. Таким образом,
в самой природе процесса измерения
заложена необратимость (стрела
времени)—различие между прошлым и
будущим. По отношению к прошлому оно
“верифицирует” (проверяет) вероятности
различных возможных состояний, а по
отношению к будущему создает новое
состояние.
,
уже не будет совпадать с результатом
первого эксперимента. Таким образом,
в самой природе процесса измерения
заложена необратимость (стрела
времени)—различие между прошлым и
будущим. По отношению к прошлому оно
“верифицирует” (проверяет) вероятности
различных возможных состояний, а по
отношению к будущему создает новое
состояние.
Таким образом, из , следует вывод о невозможности одновременного сколь угодно точного определения импульса и соответствующей координаты частицы. А это означает, что в общем случае движение частицы нельзя представить в виде фазовой траектории.
Более точные квантово механические расчеты показали, что должны выполнятся соотношения
![]() ,
,
![]() ,
,![]()
где
![]() – имеют смысл среднеквадратичных
отклонений координат и импульсов от их
средних значений (или стандартных
отклонений координат и импульсов от их
математических ожиданий) приодновременном
определении импульсов и координат (их
часто называют неопределенностями
соответствующих физических величин).
В эксперименте неопределенности—среднеквадратичные
ошибки выборочного среднего.
– имеют смысл среднеквадратичных
отклонений координат и импульсов от их
средних значений (или стандартных
отклонений координат и импульсов от их
математических ожиданий) приодновременном
определении импульсов и координат (их
часто называют неопределенностями
соответствующих физических величин).
В эксперименте неопределенности—среднеквадратичные
ошибки выборочного среднего.
Однако
можно заметить, что при наблюдениях в
пузырьковой камере (а также при движении
электронов в электронно-лучевой трубке)
явно видны треки (траектории) частиц.
Почему же тогда траектория микрочастицы
не должна существовать? Дело в том, что
при попадании электрона в пузырьковую
камеру диаметр наблюдаемых пузырьков
воздуха (![]() м)
обозначающих траекторию движения
оказывается значительно больше размера
атома (неопределенность координаты
порядка радиуса пузырька). Это означает,
что движение происходит в области
пространства, которая значительно
превышает размеры микрочастицы (
м)
обозначающих траекторию движения
оказывается значительно больше размера
атома (неопределенность координаты
порядка радиуса пузырька). Это означает,
что движение происходит в области
пространства, которая значительно
превышает размеры микрочастицы (![]() м)
и говорить о траектории частицы в строгом
смысле слова не совсем корректно. Однако
с практической точки зрения можно
полагать, что электрон движется по
траектории.
м)
и говорить о траектории частицы в строгом
смысле слова не совсем корректно. Однако
с практической точки зрения можно
полагать, что электрон движется по
траектории.
Оценим
неопределенность координаты![]() электрона в электронно-лучевой трубке,
если ось
электрона в электронно-лучевой трубке,
если ось
![]() направлена
параллельно экрану.
Найдем
неопределенность импульса
направлена
параллельно экрану.
Найдем
неопределенность импульса
![]() ,
полагая что ширина электронного луча
равна диаметру
,
полагая что ширина электронного луча
равна диаметру![]() зерна на экране монитора (или телевизора)
с электронно-лучевой трубкой длины
зерна на экране монитора (или телевизора)
с электронно-лучевой трубкой длины![]() и ускоряющим напряжением
и ускоряющим напряжением![]() :
:![]() м
м![]() кг
кг![]() м/с.
м/с.
Тогда
![]() кг
кг![]() м/с,
м/с,![]() м
м
Таким образом, хотя неопределенность координаты с практической точки зрения оказывается достаточно малой (что и позволяет рассчитывать траекторию), однако она все же значительно больше размера электрона.
Кроме , существует еще одно соотношение (имеющее несколько отличающийся смысл):
![]()
Соотношения и называются соотношениями неопределенностей Гейзенберга.
Соотношение имеет две интерпретации:
Если система находится в стационарном состоянии, то энергию системы можно измерить лишь с точностью
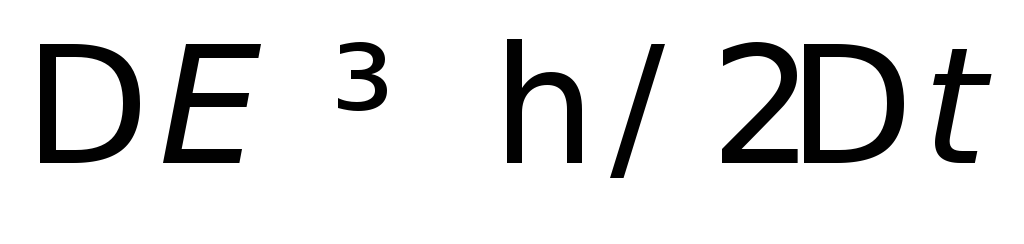 ,
где
,
где —длительность
процесса измерения. Причиной этого
является взаимодействие системы с
измерительным прибором. Энергию
взаимодействия можно учесть лишь с
точностью до
—длительность
процесса измерения. Причиной этого
является взаимодействие системы с
измерительным прибором. Энергию
взаимодействия можно учесть лишь с
точностью до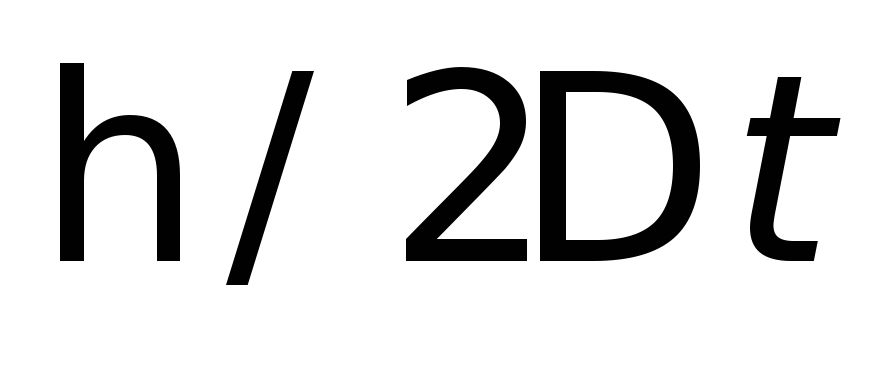 .
. –неопределенность
значения энергии нестационарного
состояния замкнутой системы,
–неопределенность
значения энергии нестационарного
состояния замкнутой системы,
 —характерное
время, в течении которого существенно
меняются средние значения физических
величин в этой системе. В этом случае
соотношение приводит следующим
выводам:
—характерное
время, в течении которого существенно
меняются средние значения физических
величин в этой системе. В этом случае
соотношение приводит следующим
выводам:
О возможности нарушения закона сохранения энергии на величину
 в течении времени
в течении времени .
Например: если в момент
.
Например: если в момент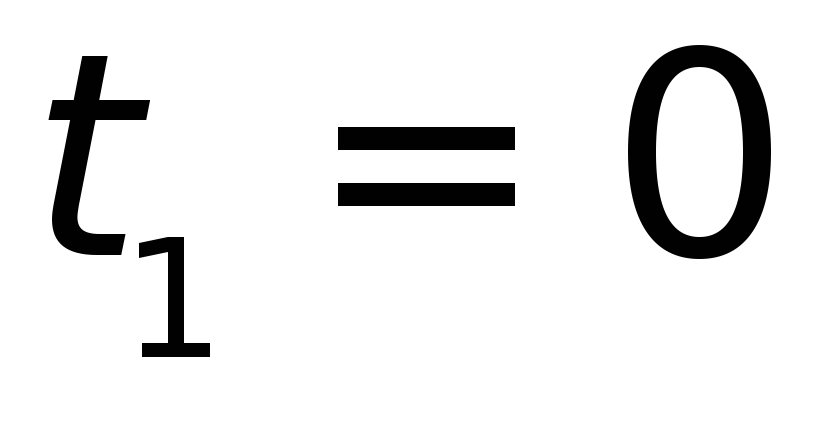 частица не существовала и ее энергия
в вакууме равнялась нулю
частица не существовала и ее энергия
в вакууме равнялась нулю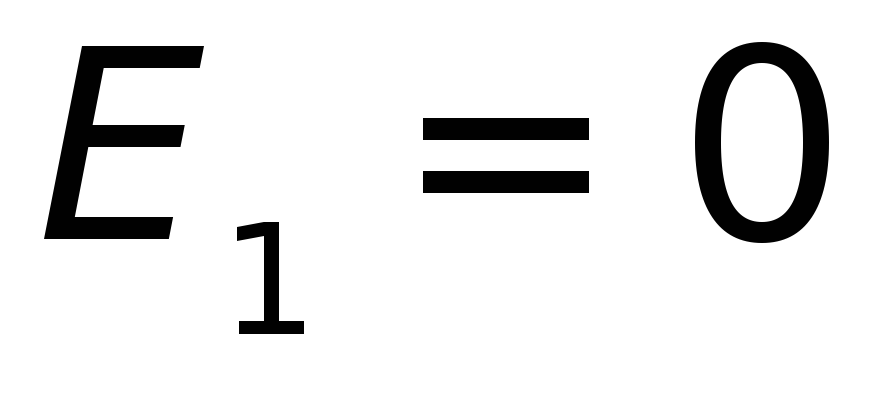 ,
затем она появилась, а в момент
,
затем она появилась, а в момент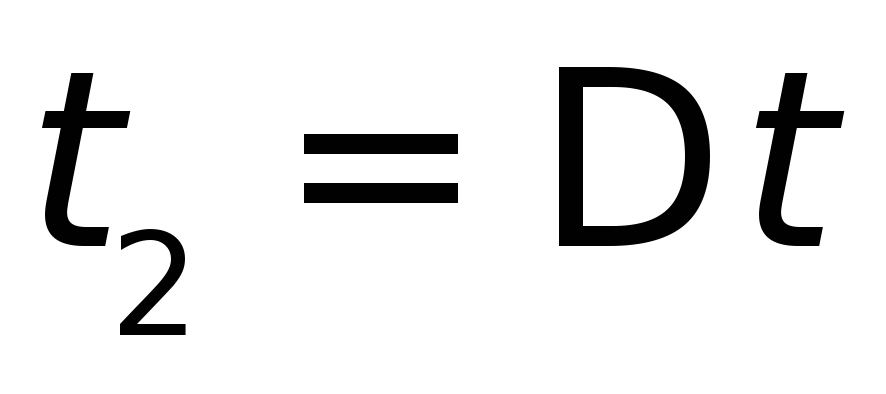 ,
когда она исчезла
,
когда она исчезла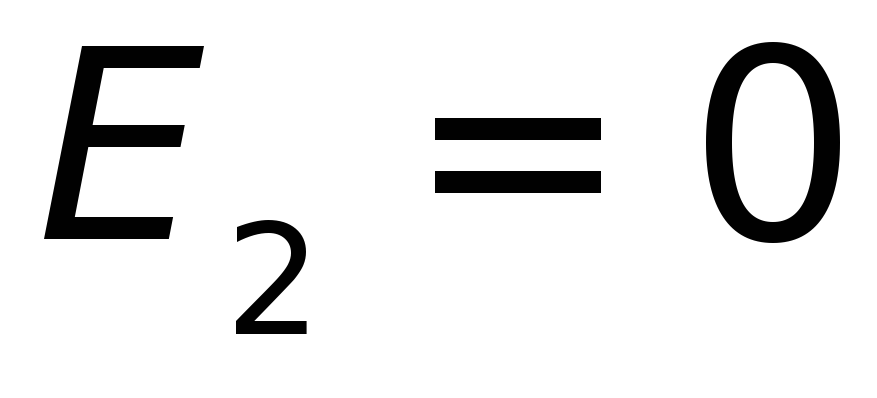 .
Тогда из следует, что в течении
.
Тогда из следует, что в течении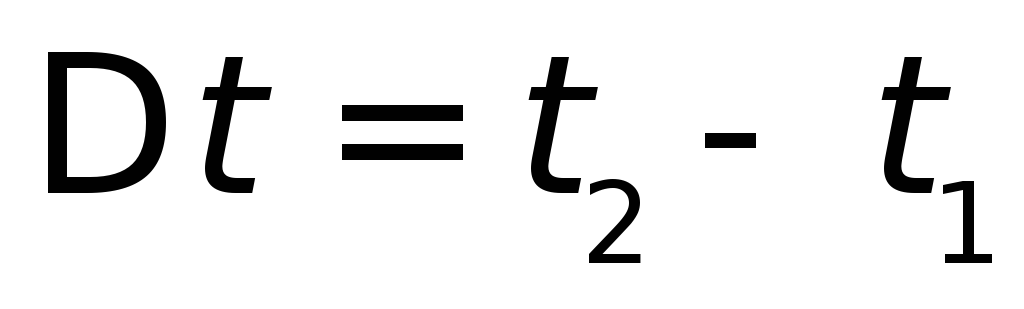 возможно нарушение закона сохранения
энергии на величину
возможно нарушение закона сохранения
энергии на величину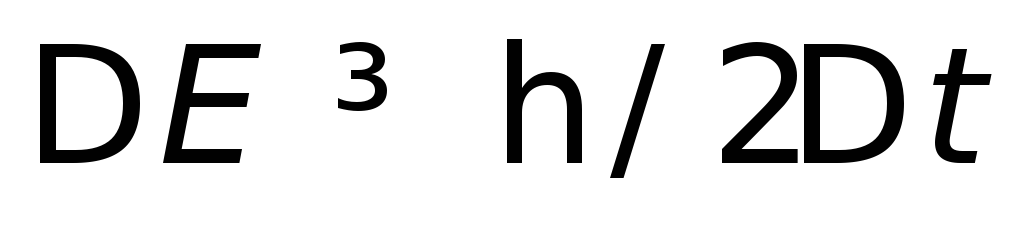 ,
которая определяет энергию родившейся
и затем исчезнувшей частицы (точнее
пары: частица–античастица). С этой
точки зрения вакуум не является пустотой:
в нем постоянно происходят процессы
рождения и уничтожения частиц. Такие
частицы называются виртуальными и не
поддаются непосредственному наблюдению,
однако проявляются себя косвенным
образом (например, вокруг электрона в
вакууме образуется облако виртуальных
позитронов, которые экранируют его
заряд). Эксперимент с двумя пластинками
в вакууме подтверждает этот вывод.
Виртуальные частицы играют особую роль
в теоретической физике: они являются
переносчиками взаимодействий. В
космологии появление виртуальных
частиц вблизи черной дыры приводит к
выводу об её излучении и испарении.
,
которая определяет энергию родившейся
и затем исчезнувшей частицы (точнее
пары: частица–античастица). С этой
точки зрения вакуум не является пустотой:
в нем постоянно происходят процессы
рождения и уничтожения частиц. Такие
частицы называются виртуальными и не
поддаются непосредственному наблюдению,
однако проявляются себя косвенным
образом (например, вокруг электрона в
вакууме образуется облако виртуальных
позитронов, которые экранируют его
заряд). Эксперимент с двумя пластинками
в вакууме подтверждает этот вывод.
Виртуальные частицы играют особую роль
в теоретической физике: они являются
переносчиками взаимодействий. В
космологии появление виртуальных
частиц вблизи черной дыры приводит к
выводу об её излучении и испарении.Если
 – время жизни частицы на энергетическом
уровне с энергией
– время жизни частицы на энергетическом
уровне с энергией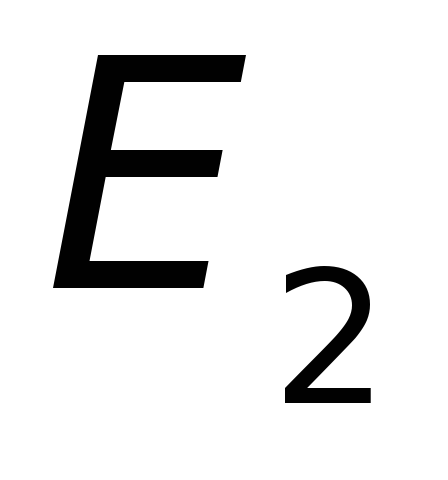 (например,
атом в возбужденном состоянии),
(например,
атом в возбужденном состоянии),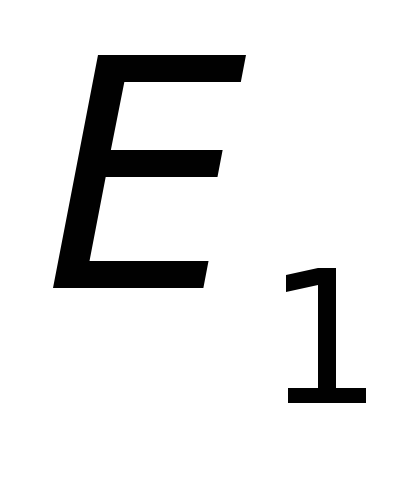 —энергия
основного состояния для которого
—энергия
основного состояния для которого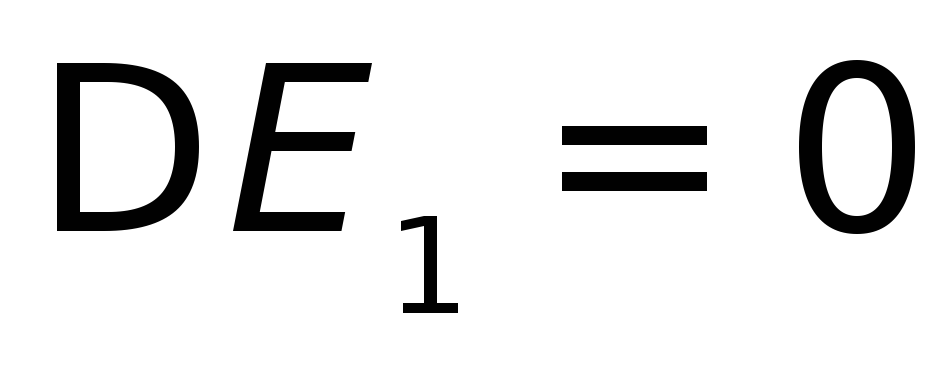 ,
тогда
,
тогда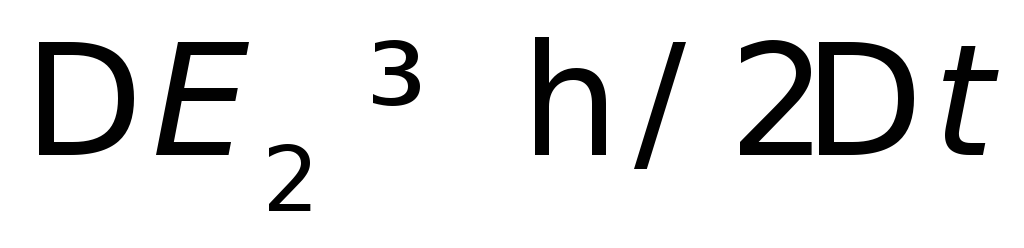 – ширина возбужденного уровня. Т.е.,
энергии возбужденных уровней не могут
быть строго определенными. Аналогично
можно получить величину энергетического
разброса испускаемых альфа частиц при
альфа-распаде.
– ширина возбужденного уровня. Т.е.,
энергии возбужденных уровней не могут
быть строго определенными. Аналогично
можно получить величину энергетического
разброса испускаемых альфа частиц при
альфа-распаде.
Соотношение
неопределенностей —фундаментальный
принцип квантовой механики, который
устанавливает содержание и структуру
ее математического аппарата. Многие
задачи квантовой механики могут быть
оценены и поняты на основе комбинации
законов классической механики с
соотношением неопределенностей. В связи
с этим рассмотрим задачу об устойчивости
атома водорода. В соответствии со вторым
законом Ньютона на электрон, движущийся
по круговой орбите с центростремительным
ускорением
![]() ,
действует сила Кулона:
,
действует сила Кулона:
![]() .
.
Если
допустить неопределенность координаты
электрона в пределах половины радиуса
орбиты
![]() ,
а неопределенность скорости в пределах
скорости
,
а неопределенность скорости в пределах
скорости![]() ,
тогда из соотношения неопределенностей
Гейзенберга следует:
,
тогда из соотношения неопределенностей
Гейзенберга следует:
![]()
Подставив в значение скорости из получим
![]() м,
м,
Следовательно,
движение электрона по орбите с
![]() (
(![]() —радиус
Бора) невозможно, электрон не может
упасть на ядро—атом устойчив.
—радиус
Бора) невозможно, электрон не может
упасть на ядро—атом устойчив.
