Федун В. И. Конспект лекций по физике Молекулярная физика и термодинамика

Лекция 17. Явления переноса.

До сих пор мы почти всегда рассматривали системы, находящиеся в состоянии термодинамического, или статистического равновесия. Однако, несмотря на безусловно важную роль равновесных состояний, они все же представляют собой особый случай. Во многих задачах, представляющих огромный физический интерес, мы имеем дело с системами, не находящимисяв равновесных состояниях.

Наука, изучающая процессы, идущие при нарушении равновесия, называется физической кинетикой.Физическая кинетика рассматривает необратимые процессы в телах, протекающие с конечными скоростями.

Рассмотрение неравновесных процессов, приводящих систему в состояние равновесия, представляет собой весьма сложную задачу. Поэтому мы подойдем к рассмотрению проблемы с помощью простейших приближенных методов, выбрав в качестве объекта исследования разреженный газ.

16. 1. Среднее число столкновений и длина свободного пробега молекул.

16. 1. Длина свободного пробега молекул.

Длиной свободного пробега называется путь, проходимый молекулой между двумя последовательными столкновениями.

Вследствие хаотичности движения различны.

Средней длиной свободного пробега молекул <>называется путь, который в среднем проходят молекулы между двумя последовательными столкновениями:

,

(16.1)

где N - число молекул.

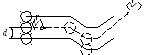
	Эффективным диаметром d молекулы называется минимальное расстояние, на которое сближаются при столкновении центры двух молекул (см. рис. 16.1). В общем случае эффективный диаметр зависит от скорости сталкивающихся молекул, т.е. от температуры газа. Эффективный диаметр молекулы уменьшается с ростом температуры, но это изменение сравнительно мало.
Рисунок 16. 1.

Значения D при нормальных условиях для некоторых газов

Газ	Воздух	Водород	Кислород	Азот
D, нм	0,27	0,28	0,36	0,58

16. 2. Среднее число столкновений молекул.

Введём понятие среднего числа столкновений <>молекулы в единицу времени.

Тогда число столкновений молекулы за время есть и оно равно отношению среднего пути молекулы к средней длине свободного пробега <>:

.

(16.2)

	Рисунок 16. 2.

Введём понятие эффективного сечения столкновения как площади поперечного сечения («коридора») ломаного цилиндра, в которой должны попасть центры соседних молекул, чтобы столкнуться с данной. Из рисунка 16.2 видно, что:

.

(16.3)

Рассчитаем число столкновений молекулы за время .

Предположим, что рассматриваемая молекула движется со скоростью , а остальные покоятся. Тогда рассматриваемая молекула столкнётся со всеми молекулами, находящимися в цилиндре площадью основания S_эфф и длиной . Число молекул, а значит и число столкновений определяется соотношением:

,

(16.4)

где n- концентрация молекул.

Чтобы учесть движение всех молекул можно, например, перейти в систему координат, связанную с движущейся молекулой, т.е. перейти от скорости к средней скорости движения молекул. Поскольку все движения молекул равновероятны, то угол между направлениями скоростей лежит в интервале () и средний угол равен . Модуль относительной скорости тогда будет:

.

(16.5)

С учётом сделанных поправок, формула () приобретает вид:

.

(16.6)

Тогда среднее число столкновений молекулы в единицу времени будет определяться выражением:

.

(16.7)

Приведённое соотношение носит название формулы Клаузиуса - Максвелла.

Чтобы найти число столкновений в единицу времени молекул газа концентрации и в объёме , т.е. для молекул газа надо величину умножить на , т.к. в каждом столкновении принимают участие 2 молекулы:

.

(16.8)

Тогда среднее число столкновений молекул в единицу времени в единичном объёме есть:

.

(16.9)

Теперь можно вернуться к средней длине свободного пробега молекулы.

За время молекула проходит путь:

,

(16.10)

и испытывает за это время число соударений, равное:

.

(16.)

Значит средняя длина свободного пробега будет равна (с учётом ()):

.

(16.)

Если учесть, что , то получаем:

.

(16.11)

Концентрация молекул связана с термодинамическими параметрами и уравнением состояния.

.

(16.12)

Тогда окончательно получаем:

.

(16.13)