Л.р.201-250 / Л_Р_237

5

Лабораторна робота №237

Вивчення власних електромагнітних коливань

Мета роботи: ознайомитися з характером власних коливань та з'ясувати основні характеристики електродинамічних коливальних систем, які визначають процес власних коливань.

Прилади й обладнання: пристрій для вивчення власних електромагнітних коливань, осцилограф.

Теоретичні відомості

В електродинаміці найпростішою коливальною системою є електричний коливальний контур, який складається з послідовно з'єднаних конденсатора С і котушки L. Якщо конденсатор зарядити до різниці потенціалів U та замкнути ланцюг, він почне розряджатися через котушку, і в колі виникне струм I, який змінюється з часом. Змінний електричний струм в контурі викликає появу змінного магнітного поля в котушці. Одночасно з цим змінюється електричне поле конденсатора. Періодичні процеси перетворення енергії електричного поля в енергію магнітного поля і навпаки називаються електромагнітними коливаннями. Час Т, протягом якого відбувається повний цикл змін у коливальному контурі, називається періодом коливання. Коливання, які відбуваються в контурі без дії на них зовнішніх ЕРС, називаються власними, або вільними електромагнітними коливаннями.

Реальний коливальний контур має електричний опір R, у наслідок чого енергія втрачається на нагрів провідників й індуктивності в з'єднуваних провідників. Знайдемо залежність сили струму від часу для ланцюга, зображеного на рис.1

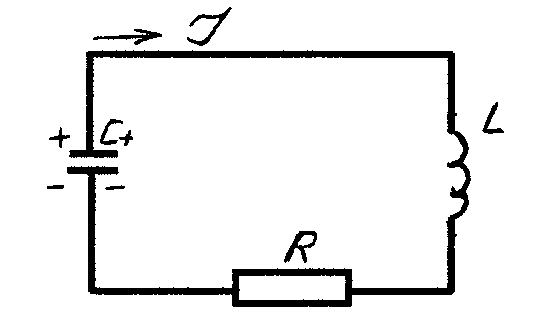
Рисунок 1

Для миттєвих значень струму за законом Ома ,

де U  напруга, обумовлена зарядами конденсатора,

e  ЕРС самоіндукції, яка виникає в котушці при протіканні в ній змінного стуму,

.

Звідси

.

Оскілбки при розряді конденсатора струм , а заряд , то

.

Поділивши цю рівність на CL і зробивши перетворення, отримаємо рівняння розряду конденсатора через індуктивність та опір у вигляді

.

(1)

Уведемо позначення , ,

де  коефіцієнт затухання,  циклічна частота власних коливань контуру (коливань без затухання).

Тоді рівняння (1) матиме вигляд

.

(2)

Це і є рівняння затухаючих коливань для напруги між обкладками конденсатора. Рівняння, аналогічне (2), можна записати для струму в контурі I та заряду q на обкладках конденсатора.

Таки чином, у процесі розрядження конденсатора через індуктивність у коливальному контурі виникають вільні затухаючі коливання струму, заряду на обкладці і напруги між обкладками конденсатора.

Якщо виконується умова , то розв'язок рівняння (2) можна записати у вигляді

,

(3)

де

(4)

циклічна частота вільних затухаючих коливань контуру.

Період затухаючих коливань визначається формулою

.

(5)

Амплітуда коливань змінюється з часом за експоненціальним законом

,

(6)

де  початкова напруга на конденсаторі (при t=0).

На рис.2 зображений графік затухаючих коливань. Графіки для заряду і сили струму мають аналогічний вид.

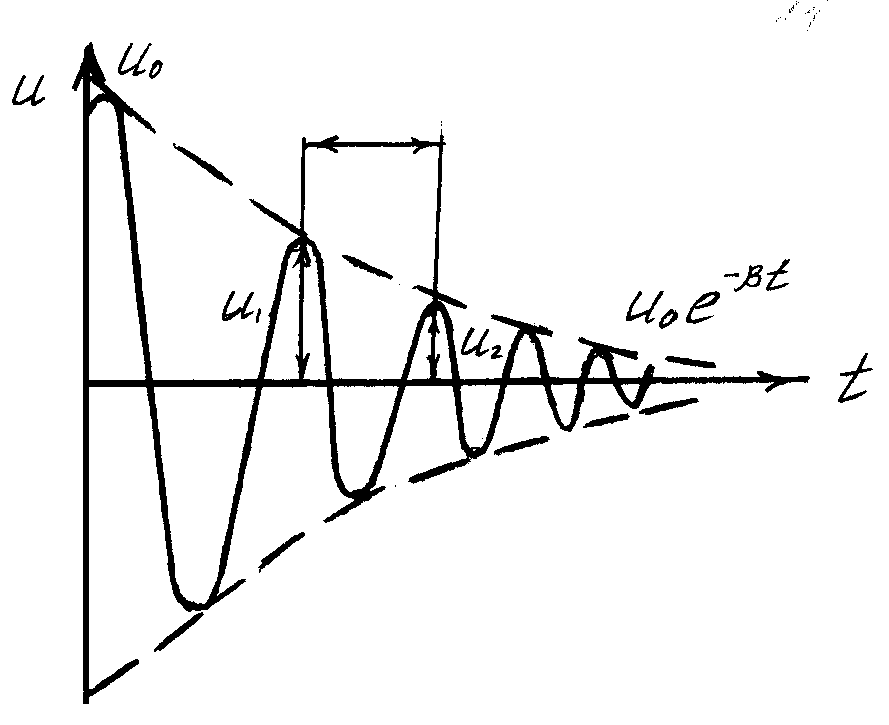
Рисунок 2

Для характеристики коливань служить логарифмічний декремент затухання l  натуральний логарифм відношення двох послідовних амплітуд та (рис. 2), відстань між якими в часі, складає один період Т:

.

(7)

На основі рівнянь (6) та (7) можна показати, що логарифмічний декремент обернено пропорційний числу коливань , які здійснюються за час, протягом якого амплітуда зменшується в е=2.72 разу, .

Коливальний контур часто характеризують його добротністю Q, яка визначається як величина, обернено пропорційна логарифмічному декременту затухання:

.

(8)

Із (6) виходить, що добротність контуру тим більша, чим більше число коливань устигає здійснитися, перш ніж амплітуда зменшиться в е разів.

Із (4) видно, що при вільні коливання в контурі не виникають. У цьому випадку .

Опір

		(9)
Рисунок 3	називається критичним опором. Якщо , розряд конденсатора носить аперіодичний характер (рис. 3). Якщо опір R контуру поступово зменшувати, О, то затухання коливань у ньому також зменшиться. При R=0 вільні електромагнітні коливання в контурі

стають незатухаючими. Згідно з рівнянням (5) при R=0 період вільних незатухаючих коливань . Ця формула називається формулою Томсона.

Опис установки

Рисунок 1

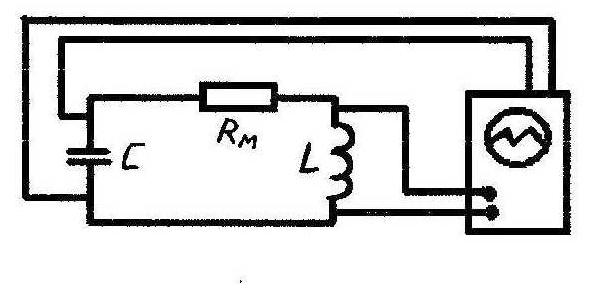
Пристрій для вивчення власних електромагнітних коливань виконаний у вигляді окремого блока і складається з коливального контуру з широким діапазоном значень ємності й опору (принципова схема пристрою наведена на рис. 1). У середині блока розміщені

циліндрична котушка з відомими індуктивністю та омічним опором, вісім різних конденсаторів з ємностями і вісім резисторів з опорами . Значення ємності та опору встановлюється обертанням ручок перемикачів, які знаходяться на верхній панелі блока, у відповідне положення.

Коливання в контурі збуджуються за допомогою генератора імпульсів осцилографа, який виробляє короткі (с) імпульси з частотою розгортки. За час між імпульсами в контурі відбуваються вільні затухаючі коливання. Напруга, яка виникає на кінцях котушки, подається через підсилювач осцилографа на пластини вертикальної розгортки, і на екрані буде спостерігатися картина затухання коливань.

Перед виконанням завдання необхідно ретельно ознайомитися з інструкцією до експлуатації осцилографа!

Порядок виконання роботи

1. Установити значення заданої викладачем ємності (С=0,5 мкф) та опір (R=470 Ом).

2. Натиснути кнопки “Грубо” (10 Гц) і “Синхр”.

3. Регулятор частоти плавно повернути за годинниковою стрілкою до одержання чіткої картини затухаючих коливань.

4. Замалювати картинку, що спостерігається на екрані осцилографа.

5. Порахувати кількість коливань n і за формулою обчислити період власних коливань (). Дані записати в таблицю 1.

Таблиця 1

№ п/п		n	T, c	L, Гн	С, Ф	R, Ом	, с	, %
1
2
3
сер

6. Визначити теоретичне значення періоду за формулою

.

7. За формулою обчислити відносну похибку.

8.Змінити значення R і повторити пп.37. Дані вимірів і обчислень записати в таблицю 1.

9.Змінити значення С і повторити пп.37.

10.За картинками затухаючих коливань 13 дослідів визначити початкову амплітуду А₀ та амплітуду через n коливань А_n й обчислити логарифмічний декремент затухання за формулою

.

11. Обчислити теоретичне значення логарифмічного декременту затухання за формулою

.

Значення L, C, R узяти з таблиці 1.

12. Порівняти експериментальне й теоретичне значення логарифмічних декрементів затухання та обчислити відносну похибку

.

Дані обчислень занести в таблицю 2.

Таблиця 2

№ п/п	А0	Аn	n	R, Ом	L, Гн	С, Ф			, %
1
2
3
сер

13.Зробити висновок.

Контрольні питання

1. Поясніть механізм виникнення електромагнітних коливань у контурі.

2. Як визначаються частота і період коливань у контрі?

3. Що називають логарифмічним декрементом затухання?

4. Що називають критичним опором?
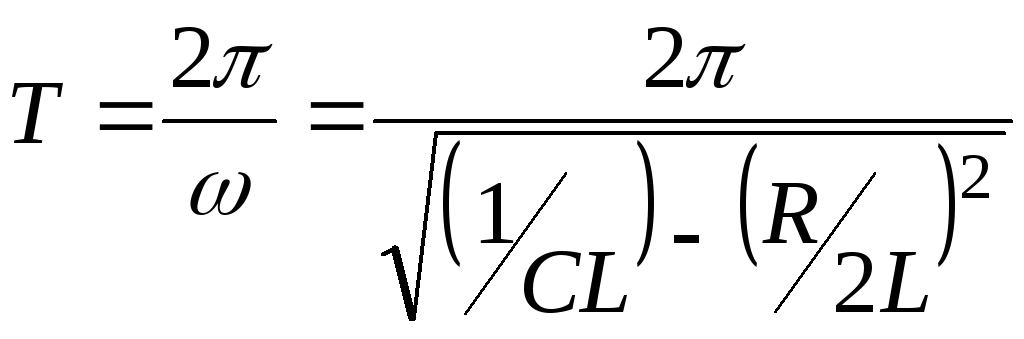