
- •Навчальний посібник з фізики
- •Розділ і. Механіка
- •1.1. Основи кінематики
- •1.2. Основи динаміки
- •1.3. Закони збереження в механіці.
- •Розділ іі. Молекулярна фізика
- •2.2. Основи термодинаміки.
- •Загальні рекомендації до розв’язання задач
- •Основні формули з розділу «Механіка»
- •Кінематичне рівняння рівномірного руху матеріальної точки вздовж осі х:
- •Задачі для самостійного розв’язування з розділу «Механіка»
- •Основні формули з розділу «Молекулярна фізика та термодинаміка»
- •Приклади розв’язування задач
- •Література
Основні формули з розділу «Механіка»
Середня
швидкість і середнє прискорення:
 ;
; ,
,
де S - шлях, пройдений точкою за інтервал часу t.
Шлях S, на відміну від різниці координат, x = x2 – x1 не може приймати негативні значення, тобто S0.
Миттєва швидкість і миттєве прискорення при прямолінійному русі:
 ,
,
 ,
,
де
Д –
вектор
переміщення.
–
вектор
переміщення.
Якщо прискорення однакове в усіх точках шляху і в будь-який момент часу, то рух буде рівнозмінним.
Кінематичне рівняння рівномірного руху матеріальної точки вздовж осі х:
 ,
,
де x0 – початкова координата.
При
рівномірному
русі
 .
.
Кінематичне рівняння рівнозмінного руху матеріальної точки уздовж осі X:
 ,
,
де хо – початкова координата рухомої точки у момент часу t = 0;
 о
–
швидкість точки в даний момент часу;
о
–
швидкість точки в даний момент часу;
а – прискорення.
Швидкість і шлях рівнозмінного поступального руху:
 .
.
Швидкість і переміщення при вільному падінні:
 ,
,
де g – прискорення вільного падіння.
Кутова швидкість і кутове прискорення при обертальному русі:
 ;
;
 .
.
Кінематичне рівняння рівнозмінного обертального руху:

Зв'язок між лінійними і кутовими величинами при обертальному русі:
 ,
S
–
довжина дуги, пройдена точкою, – кут
обертання точки,
R
–
радіус обертання точки;
,
S
–
довжина дуги, пройдена точкою, – кут
обертання точки,
R
–
радіус обертання точки;
 ;
;
 ;
; .
.
Імпульс (кількість руху) матеріальної точки масою m, що рухається зі швидкістю:
 .
.
Основне рівняння динаміки поступального руху:
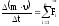 .
.
Сили, що розглядаються в механіці:
а) сила пружності:
 ,
,
де k – коефіцієнт пружності; x – абсолютна деформація.
Механічна
напруга
при пружній деформації тіла:
 ,
,
де F - сила, що розтягує або стискає тіло; S - площа поперечного перерізу тіла.
Відносне
поздовжнє розтягування
(стиснення):
 ,
,
де
 –
зміна довжини тіла при розтягуванні
(стисненні);
–
зміна довжини тіла при розтягуванні
(стисненні); - довжина тіла до деформації.
- довжина тіла до деформації.
Закон
Гука
для поздовжнього розтягування (стиснення):
 ,
,
де
 -
модуль Юнга.
-
модуль Юнга.
б) сила тертя ковзання:
 ,
,
де µ – коефіцієнт тертя; N – сила нормальної реакції опори.
в) сила гравітаційної взаємодії (сила тяжіння):
 ,
,
де G – гравітаційна стала; m1 і m2 – маси взаємодіючих тіл; r – відстань між тілами (тіла розглядаються як матеріальні точки);
г) чисельне значення сили, що діє на тіло, яке рухається по дузі кола радіусом R:
 .
.
Закон збереження імпульсу (кількості руху) для замкненої (ізольованої) системи:
 ,
,
або для двох тіл (i = 2):
 ,
,
де
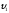 і
і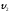 – швидкості тіл до взаємодії;
– швидкості тіл до взаємодії;
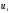 і
і
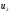 – швидкості тих же тіл після їх взаємодії.
– швидкості тих же тіл після їх взаємодії.
Кінетична енергія тіла:
 .
.
Потенціальна енергія:
а) пружно деформованого тіла:
 ,
,
де k – коефіцієнт пружності (жорсткість) тіла; x – абсолютна деформація;
б) тіла, піднятого над поверхнею Землі:
 ,
,
де g – прискорення вільного падіння; h – висота тіла над рівнем, прийнятим за нульовий (формула справедлива за умови h<<RЗ, де RЗ – радіус Землі).
Закон збереження повної механічної енергії (для замкненої системи, де діють консервативні сили):
W = Wк+WП = const.
Робота А, здійснювана зовнішніми силами, визначається як міра зміни кінетичної енергії системи (тіла): A = W = W2 - W1
Робота:
а) постійної сили F:
 ,
,
де
- кут між напрямами сили
 і переміщення
і переміщення ;
;
б) пружної сили:
 .
.
Потужність:
 .
.
Момент сили відносно нерухомої осі обертання:
M = F d, де d=r∙sinα – плече сили F.
Кінематичне рівняння гармонійних коливань матеріальної точки:
 ,
,
де х – зсув точки, що коливається, від положення рівноваги;
А – амплітуда коливань;
– кругова або циклічна частота;
0 – початкова фаза коливань;
t – час.
Періодом коливань називається проміжок часу між двома послідовими максимальними відхиленнями фізичної системи від положення рівноваги.
Зв’язок між періодом коливань та циклічною частотою ω:
 ,
,
де Т – період коливань точки; v – частота коливань.
Повна енергія точки, що коливається:
W
= Wк+WП
=
 .
.
Період власних коливань:
а) математичного маятника
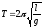 ,
,
де l – довжина маятника; g – прискорення вільного падіння;
б) пружинного маятника

де m – маса тіла, що коливається; k – жорсткість пружини.
Довжина хвилі
 ,
,
де Т – період коливання;
 –швидкість
розповсюдження хвилі;
–швидкість
розповсюдження хвилі;
v – частота коливань.
Приклади розв`язування задач
ЗАДАЧА 1
Автомобіль першу половину шляху рухався зі швидкістю 72 км/год. Потім половину часу він рухався зі швидкістю 42 км/год, а іншу половину часу зі швидкістю 30 км/год. Визначити середню швидкість руху автомобіля.
|
Дано:
|
Розв'язок:
Середня
швидкість руху:
|
|
|
З урахуванням цього:
t
= t1+
2t2
=
визначимо середню швидкість руху:
 сер
сер

скоротимо чисельник і знаменник на S1 i будемо мати:
![]() сер
=
сер
=

Обчислимо:
![]() сер=
сер=![]()
 (км/год)
(км/год)
Вiдповiдь:
 сер=48
км/год
сер=48
км/год
ЗАДАЧА 2
З
яким прискоренням зісковзує тiло з
похилої площини з кутом нахилу
![]() ,
якщо з похилої площини з кутом нахилу
,
якщо з похилої площини з кутом нахилу![]() воно рухається вниз рiвномiрно?
воно рухається вниз рiвномiрно?
Дано: Розв'язок:
|
< α < β |
|
а - ? |
На
тiло дiють три сили: сила тяжiння 
 сила
нормальної реакції опори
сила
нормальної реакції опори
 з боку похилої площини i сила тертя
з боку похилої площини i сила тертя тер.
Якщо по похилiй площинi з кутом нахилу
тер.
Якщо по похилiй площинi з кутом нахилу
![]() тiло рухається рiвномiрно , то прискорення
а = 0 i вiдповiдно:
тiло рухається рiвномiрно , то прискорення
а = 0 i вiдповiдно:
 тер
=0 (1)
тер
=0 (1)
Виберемо дві взаємно перпендикулярні вісі координат OX та OY і запишемо рівняння (1) в проекціях на ці вісі:

Так
як сила тертя Fтер
= ,
,
де
![]() -
коефіцієнт тертя ковзання, то: Fтер
=
-
коефіцієнт тертя ковзання, то: Fтер
=![]() mg
cos
mg
cos![]() .
.
Підставимо значення Fтер в рівняння (2):
mg
sin![]() -
-![]() mg
cos
mg
cos
 =0
(4)
=0
(4)
з
рівняння (4) випливає, що
![]() =tg
=tg
 (5)
(5)
Пам'ятаємо, що коефіцієнт тертя залежить від матеріалу стикових поверхонь тіл і тому буде однаковим в першому і другому випадках.
Якщо
тіло рухається з прискоренням по похилій
площині з кутом нахилу
 ,
то на підставі другого закону Ньютона:
,
то на підставі другого закону Ньютона:

 тер;
(6)
тер;
(6)
в проекціях на вісі координат:
ma=mg
sin![]() - Fтер
(7)
- Fтер
(7)
0=mg
cos![]() - N (8)
- N (8)
З
рівняння (8) маємо: N=mg cos![]() ,
,
з
урахуванням цього: Fтер
=![]() mg
cos
mg
cos![]() .
.
Підставимо
значення
![]() з (5):
з (5):
F
=tg![]() mg
cos
mg
cos![]() . З (7) будемо мати: ma=mg sin
. З (7) будемо мати: ma=mg sin![]() -
tg
-
tg![]() mg
cos
mg
cos![]() ,
або остаточно: a=g sin
,
або остаточно: a=g sin![]() -
gtg
-
gtg![]() cos
cos![]() .
.
Відповідь:
a=g
(sin![]() -
tg
-
tg![]() cos
cos![]() ).
).
ЗАДАЧА 3
Радіус
малої планети 250 км, середня густина![]()
 .
Визначити прискорення вільного падіння
на поверхні цієї планети.
.
Визначити прискорення вільного падіння
на поверхні цієї планети.
Дано: Розв'язок:
|
|
|
gn -? |
За
законом всесвітнього тяжіння на тіло
масою m на цій планеті діє сила
 ,
,
де G - гравітаційна стала,
G=
 ;
mn
- маса планети;
;
mn
- маса планети;
R
- радіус планети. Позначимо прискорення
вільного падіння на цій планеті gn.
Тоді:
 ,
або
,
або .
Масу планети можна визначити за формулою:
.
Масу планети можна визначити за формулою: ,
де
,
де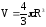 - об'єм планети.
- об'єм планети.
З
урахуванням цього:
 .
.
Обчислимо:

Відповідь:
gn
= 0,21
 .
.
ЗАДАЧА 4
Снаряд
масою m=5
кг, що вилетів з гармати, у верхній точці
траєкторії має швидкість
 =300
м/с. У цій точці він розірвався на 2
осколки, причому більший осколок масоюm1=3
кг рухається в зворотному напрямку зі
швидкістю
=300
м/с. У цій точці він розірвався на 2
осколки, причому більший осколок масоюm1=3
кг рухається в зворотному напрямку зі
швидкістю
 1=100
м/с. Визначити швидкість
1=100
м/с. Визначити швидкість
 2
другого, меншого осколка.
2
другого, меншого осколка.
Дано: Розв'язок:
|
m=5 кг
m1=3 кг
|
|
|
Запишемо
закон збереження імпульсу для непружного
удару в умовах даної задачі: m =m1
=m1 1+m2
1+m2 2
2
В
скалярному
вигляді: m =
–m1
=
–m1 1+m2
1+m2 2.
(1)
2.
(1)
Масу другого осколка знайдемо за різницею мас снаряду та першого осколка: m2=m –m1. (2)
Підставимо
(2) в (1):
 .
Зробимо обчислення:
.
Зробимо обчислення: (м/с).
(м/с).
Відповідь:
 2=60
м/с.
2=60
м/с.
ЗАДАЧА 5
До нижнього кінця вертикального дроту завдовжки 5 м і площею поперечного перерізу 2 мм2 підвішено вантаж 5,1 кг, внаслідок чого дріт видовжився на 0,6 мм. Визначити модуль Юнга для матеріалу дроту.
Дано: Розв'язок:
|
S = 2 мм m = 5,1 кг
|
Визначимо
механічну напругу:
визначимо
відносне видовження дроту:
З
формули
Обчислимо:
Відповідь:
|
|
Е - ? |



