§ 1. Числові ряди. Збіжність числового ряду.

1. Якщо — нескінченна числова послідовність, то символ суми всіх її членів, тобто вираз виду

називають числовим рядом. Числа називають членами ряду, а — загальним членом ряду.

2. Суму перших n членів ряду (1) називають n-ю частковою сумою ряду і позначають , тобто :

(2)

(3)

Часткові суми числового ряду (1) утворюють нескінченну числову послідовність

. (4)

3. Якщо послідовність (4) часткових сум числового ряду (1) має скінченну границю при , тобто

то кажуть, що ряд (1) збіжний, а число S називають сумою ряду (1).

Якщо ж послідовність (4) не має скінченної границі при , то кажуть, що ряд (1) розбіжний. В цьому випадку не варто говорити про суму ряду.

Приклад 1. Дослідити на збіжність ряд

Розв’язання. Заданий ряд є сумою членів геометричної прогресії з першим членом і знаменником . Відомо, що сума n перших членів геометричної прогресії обчисляється за формулою . Таким чином n-а часткова сума заданого ряду матиме вигляд:

.

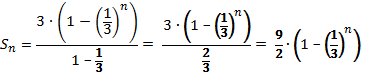При послідовність часткових сум заданого ряду має скінчену границю:

Отже, заданий ряд збіжний його сума S=4,5.

Приклад 2. Дослідити на збіжність ряд

Розв’язання. Заданий ряд є сумою членів арифметичної прогресію з першим членом і різницею . Відомо, що сума n перших членів арифметичної прогресію обчислюється за формулою . Таким чином n-a часткова сума заданого ряду матиме вигляд :

При послідовність часткових сум заданого ряду не має скінченної границі:

Отже, заданий ряд розбіжний.

4. Властивості збіжних рядів:

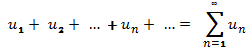
1. Якщо ряд збіжний і має суму S, a 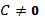– стала, то ряд 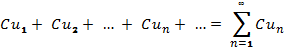теж збіжний і має суму CS.

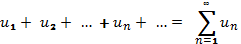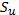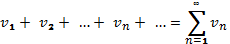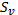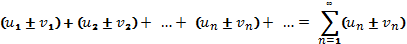2. Якщо ряд збіжний і має суму , а ряд збіжний і має суму , то ряд теж збіжний і має суму .

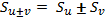3. Ряд, утворений шляхом відкидання або дописування будь-якого скінченного числа членів до збіжного ряду, теж буде збіжним.

5. Якщо всі члени ряду (1) задовольняють умову , то цей ряд називають рядом з додатними членами.

§2. Ознаки збіжності числових рядів

1. Необхідна ознака Збіжності числового ряду. Якщо ряд

збіжний, то

Наслідок. Якщо

то ряд (1) розбіжний.

2. Зауваження. З виконання умови

не випливає збіжність ряду (1) .

Приклад 1. Перевірити виконання необхідної умови збіжності для ряду

Розв’язання. Заданий ряд називають гармонійним рядом. Знаходимо

Отже необхідна умова збіжності ряду виконується. Але, це не означає, що заданий ряд збіжний. Як буде показане далі, гармонійний ряд — розбіжний (див. приклад 9).

Приклад 2. Перевірити виконання необхідної умови збіжності для ряду

Розв’язання. Оскільки

то необхідна умова збіжності не виконується. Це означає, що заданий ряд розбіжний (див. п.1, наслідок)

3. Перша ознака порівняння рядів. Нехай

ряди з додатними членами. Якщо ряд

збіжний і, починаючи з деякого члена, для кожного члена ряду

виконується нерівність , то ряд

теж збіжний.

4. Друга ознака порівняння рядів. Нехай

ряди з додатними членами. Якщо ряд

розбіжний і , починаючи з деякого члена, для кожного члена ряду

виконується нерівність , ряд

теж розбіжний.

5. Третя ознака порівняння рядів. Якщо для рядів

існує скінченна відмінна від нуля границя відношення їх загальних членів при , тобто

то ці ряди або обидва збіжні, або обидва розбіжні.

Приклад 3. Дослідити на збіжність ряд

Розв’язання. Порівняємо заданий ряд з сумою геометричної прогресії

Очевидно, що (2) і (3) — ряди з додатними членами. Ряд (3) збіжний, бо знаменний прогресії . Очевидно, що всі члени ряду (2) не перевищують відповідних членів ряду (3) . Отже, за першою ознакою порівняння рядів (див. п.3), ряд (2) — збіжний.

Приклад 4. Дослідити на збіжність ряд

Розв’язання. Кожен член заданого ряду не менший ніж відповідний член гармонійного ряду, який розбіжний (див. приклад 9). Тому, за другою ознакою порівняння рядів (див. п.4) , ряд (4) теж розбіжний ( робили такий висновок, ми враховуємо, що обидва розглядувані ряди є рядами з додатними членами).

Приклад 5. Дослідити на збіжність ряд

Розв’язання. Загальний член заданого ряду , загальний член гармонійного ряду . Оскільки гармонійний ряд розбіжний і за першою визначною границею

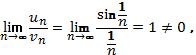
то за третьою ознакою порівняння рядів (див. п.5) , ряд (5) теж розбіжний.

Приклад 6. Дослідити на збіжність ряд

Розв’язання. Загальний член заданого ряду , загальний член ряду (2) . Оскільки

і ряд (2) збіжний (див. приклад 3), то за третьою ознакою порівняння рядів (див п.5) заданий ряд теж збіжний.

6. Ознака Даламбера. Якщо

ряд з додатними членами і існує скінченна границя

1. при 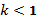, цей ряд збіжний;

2. при 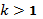, цей ряд розбіжний;

3. при 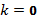, цей ряд може бути як збіжним, так і розбіжним, в такому разі слід скористатися іншими ознаками збіжності рядів.

Приклад 7. Дослідити на збіжність ряд :

Розв’язання. Очевидно, що заданий ряд є рядом з додатними членами. Для нього

Оскільки , то за ознакою Даламбера (див. п. 6(1)), заданий ряд збіжний…

Приклад 8. Дослідити на збіжність ряд :

Розв’язання. Очевидно, що заданий ряд є рядом з додатними членами. Для нього :

За другою визначною границею :

Оскільки , то, за ознакою Даламбера (див. п.6 (2)), заданий ряд розбіжний.

7. Інтегральна ознака Коші. Якщо функція неперервна, додатна і спадна на проміжку , то числовий ряд

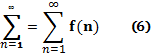
збіжний, якщо існує скінченна границя

Ряд (6) розбіжний, якщо вказана границя не існує, тобто вказаний невласний інтеграл розбіжний.

Приклад 9. Дослідити на збіжність гармонійний ряд

Розв‘язання. Заданий ряд можна подати у такому вигляді

Тоді 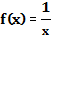. Ця функція неперервна, додатна і спадна на проміжку . Розглянемо невласний інтеграл:

Невласний інтеграл

розбіжний, то, за інтегральною ознакою Коші, гармонійний ряд

теж розбіжний.

Приклад 10. Дослідити на збіжність ряд

Розв’язання. Заданий ряд можна подати у такому вигляді:

Тоді . Ця функція неперервна, додатна і спадна на проміжку .

1. Нехай p=1. Тоді ми отримаємо гармонійний ряд, який є розбіжним (див. приклад 9).

2. Нехай p>1 . Розглянемо невласний інтеграл:

Знаходячи цю границю, ми скористалися тим, що при

Таким чином, при p > 1 : невласний інтеграл

збіжний, то за інтегральною ознакою Коші заданий ряд теж збіжний.

3. Нехай p < 1. Розглянемо невласний інтеграл:

Знаходячи цю границю, ми скористалися тим, що при

Таким чином невласний інтеграл

розбіжний, то за інтегральною ознакою Коші заданий ряд теж розбіжний.

Отже, заданий в умові задачі ряд збіжний при p > 1 і розбіжний при p ≤1. Цей ряд часто використовують для порівняння з іншими рядами в разі дослідження питання про їх збіжність.

8. Радикальна ознака Коші. Якщо

ряд додатними членами і існує скінченна границя

то:

1. при k < 1, цей ряд збіжний;

2. при k > 1, цей ряд розбіжний;

3. при k = 0, цей ряд може бути як збіжним, так і розбіжним, в такому разі слід скористатися іншими ознаками збіжності рядів.

Приклад 11. Дослідити на збіжність ряд

Розв‘язування. Заданий ряд є рядом з додатними членами. Його загальний член . Знаходимо:

Оскільки k < 1, то за радикальною ознакою Коші ряд збіжний.