До розрахунку параметрів лінійної регресії, теоретичних рівнів і залишкових величин

Номер господар- ства	Кількість внесених добрив х, д. р	Урожайність зернових у, ц/га	ху	х2	Y	y – Y	(y – Y)2
1	1,1	23	25,3	1,21	24	–1	1
2	1,4	25	35,0	1,96	27	–2	4
3	1,2	26	31,2	1,44	25	1	1
4	2,0	33	66,0	4,00	33	0	0
5	1,5	27	40,5	2,25	28	–1	1
6	1,3	2,8	36,4	1,69	26	2	4
7	1,8	30	54,0	3,24	31	–1	1
8	1,7	32	54,4	2,89	30	2	4
Разом	12,0	224	342,8	18,68	224		16

Користуючись цими величинами, визначаємо:

(ц/га);

.

Отже, рівняння регресії має вигляд

,

тобто кожний центнер внесених добрив (у перерахунку на діючу поживну речовину) дає приріст урожайності в середньому 10 ц/га. Якщо добрива зовсім не вносити (х = 0), то урожайність зернових не перевищить 13,0 ц/га.

Рівняння регресії відбиває закон зв’язку між х і у не для окремих елементів сукупності, а для сукупності в цілому; закон, який абстрагує вплив інших факторів, виходить з принципу «за інших однакових умов». За цих умов очікувана врожайність зернових при внесенні добрив у обсязі 1,1 ц д. р. на 1 га становить Y = 13 + 10  1,1 = 24 (ц/га). Для інших значень факторної ознаки х теоретичні рівні врожайності наведено в табл. 7.3. Вплив інших окрім х факторів зумовлює відхилення емпіричних значень у від теоретичних у той чи інший бік. Відхилення (y – Y) називають залишками і позначають символом е. Залишки, як правило, менші за відхилення від середньої, тобто .

У нашому прикладі

, .

Відповідно загальна дисперсія врожайності

,

залишкова дисперсія

.

У невеликих за обсягом сукупностях коефіцієнт регресії схильний до випадкових коливань. Тому слід перевірити його істотність. Коли зв’язок лінійний, істотність коефіцієнта регресії перевіряють за допомогою t-критерію (Стьюдента), статистична характеристика якого для гіпотези визначається відношенням коефіцієнта регресіїb до власної стандартної похибки тобто.

Стандартна похибка коефіцієнта регресії залежить від варіації факторної ознаки залишкової дисперсіїі числа ступенів свободи, деm — кількість параметрів рівняння регресії:

.

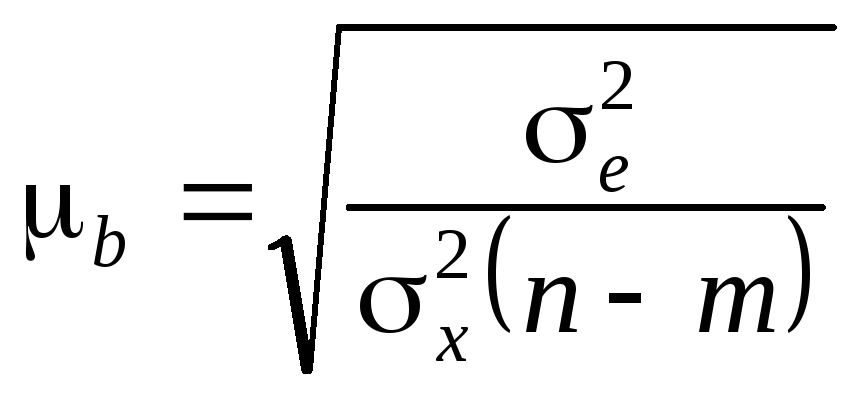Для лінійної функції m = 2. За даними табл. 7.3 маємо:

.

Звідси (ц/га), а, що перевищує критичне значення двосторонньогоt-критерію (табл. 6.3). Гіпотеза про випадковий характер коефіцієнта регресії відхиляється, а отже, з імовірністю 0,95 вплив кількості внесених добрив на врожайність зернових визнається істотним.

Для коефіцієнта регресії, як і для будь-якої іншої випадкової величини, визначаються довірчі межі . У нашому прикладі довірчі межі коефіцієнта регресії з імовірністю 0,95 (t = 2,45) становлять .

Важливою характеристикою регресійної моделі є відносний ефект впливу фактора х на результат у — коефіцієнт еластичності:

.

Він показує, на скільки процентів у середньому змінюється результат у зі зміною фактора х на 1%. У нашому прикладі тобто збільшення кількості внесених добрив на 1% спричинює приріст урожайності зернових у середньому на 0,8%.

Оцінити відносний ефект впливу фактора х на результат у можна безпосередньо на основі степеневої функції Y = ax^b, параметр b якої є коефіцієнтом еластичності. Степенева функція зводиться до лінійного виду логарифмуванням lg Y = lg a + b lg x. До класу степеневих належать функції споживання, виробничі функції тощо.