Формулы для заучивания

Формулы сокращенного умножения

1. Формула разности квадратов: .

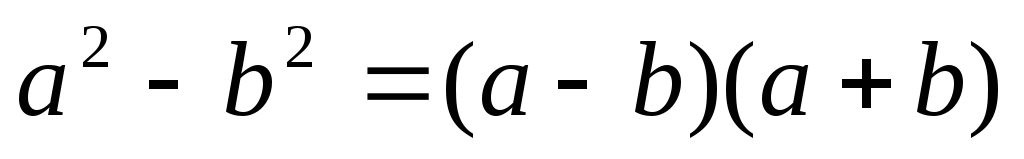2. Формула квадрата суммы: .

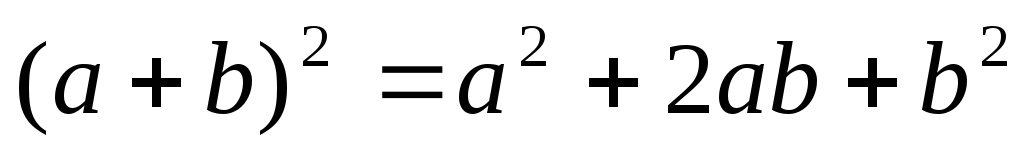3. Формула квадрата разности: .

4. Формула куба суммы: .

5. Формула куба разности: .

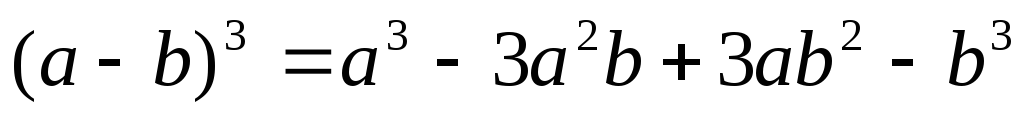6. Формула суммы кубов: .

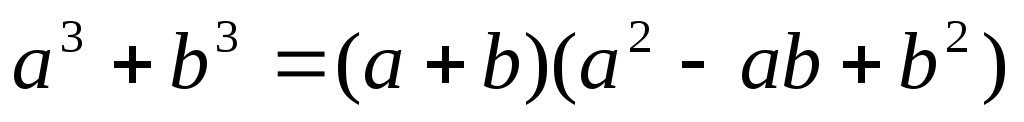7. Формула разности кубов: .

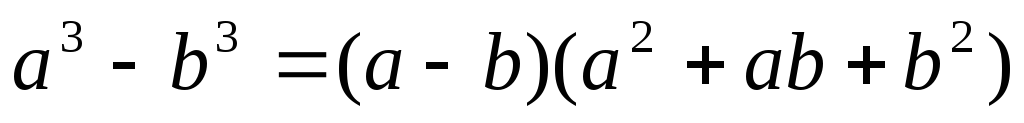Обобщения формул сокращенного умножения

1.

2.

3. Формула бинома Ньютона:

,

где , , ; ;

Свойства логарифмов

1. Основное логарифмическое тождество: .

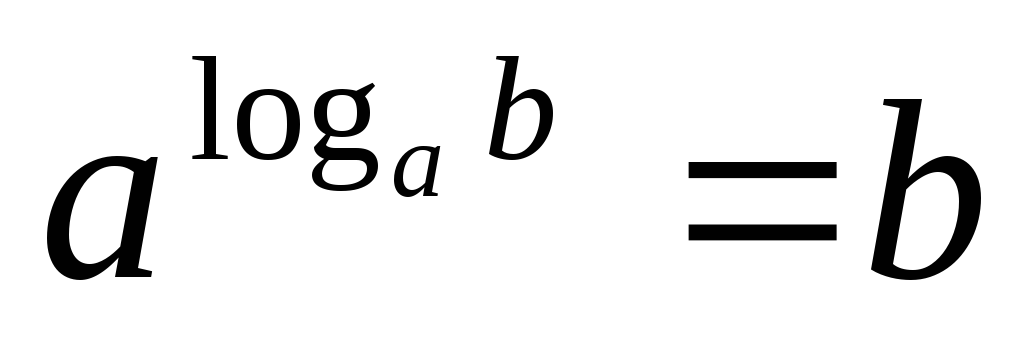2. Логарифм произведения: .

3. Логарифм частного: .

4. Логарифм степени: .

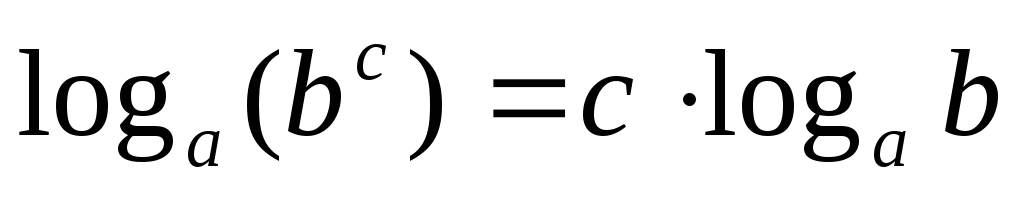5. Формула перехода к новому основанию: .

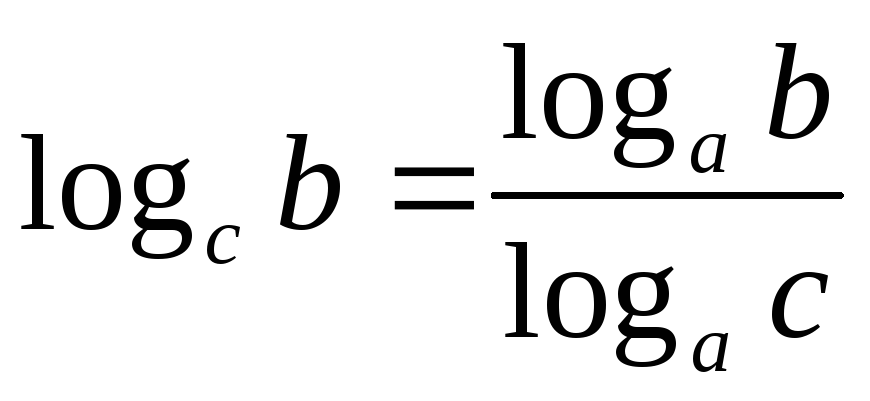6. Формула связи:

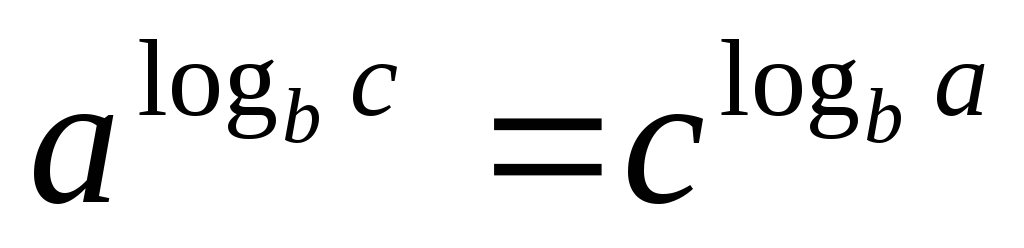
Свойства степеней

1. Умножение степеней с одинаковым основанием: .

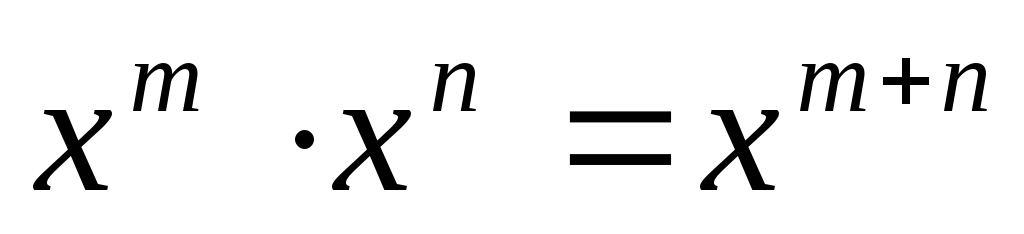2. Деление степеней с одинаковым основанием: .

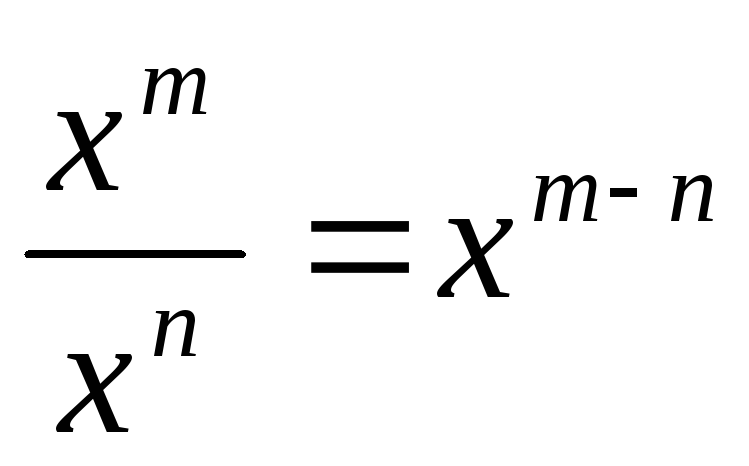3. Возведение степени в степень: .

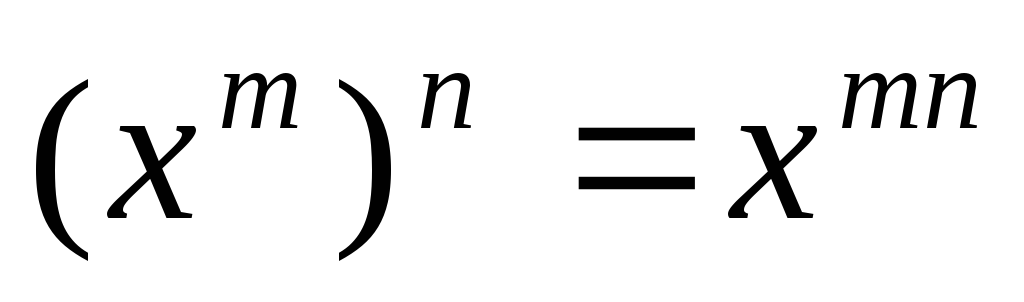4. Умножение степеней с разными основаниями, но одинаковыми показателями:.

5. ,

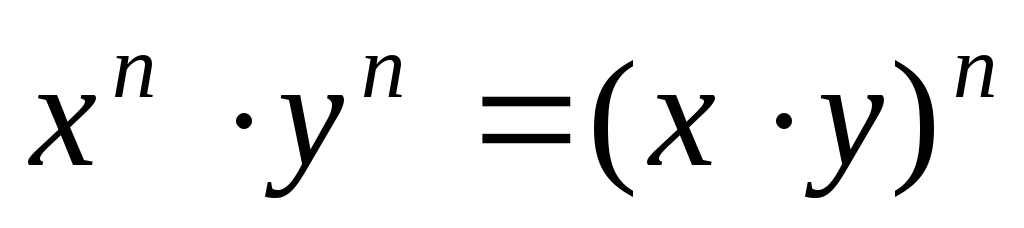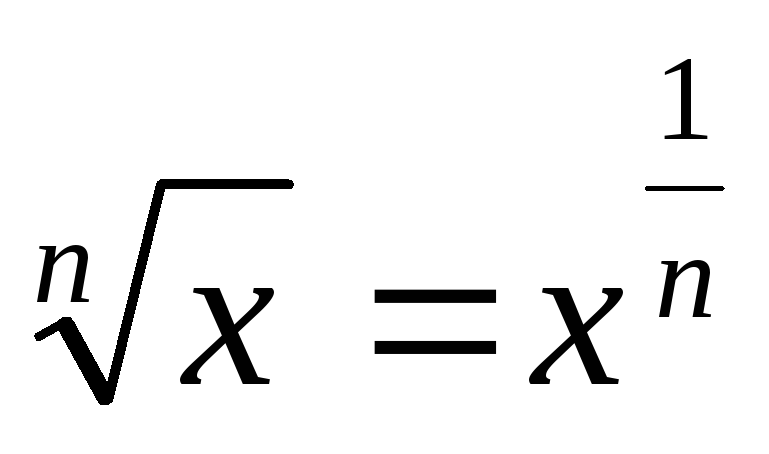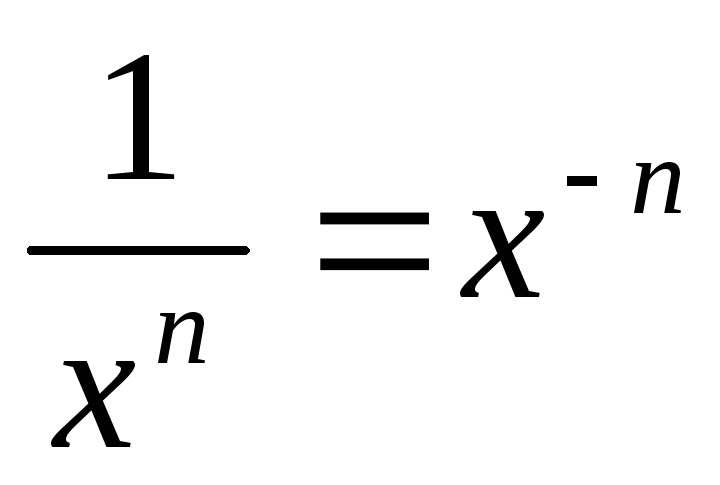
Формулы тригонометрии

1. Нечетность синуса , четность косинуса .

2. Синус суммы: .

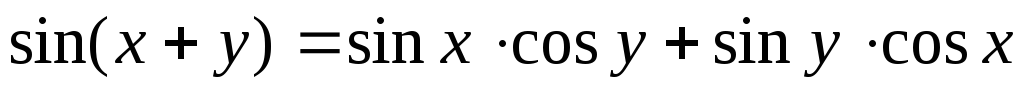3. Синус разности: .

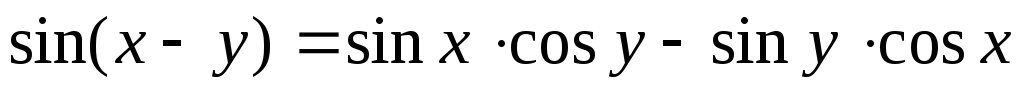4. Косинус суммы: .

5. Косинус разности: .

6. Основное тригонометрическое тождество: .

7. Синус двойного угла: .

8. Косинус двойного угла: .

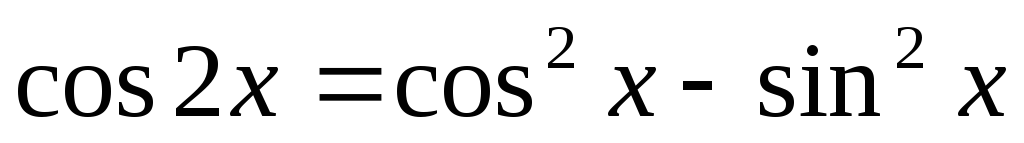9. Формулы понижения: степени:.

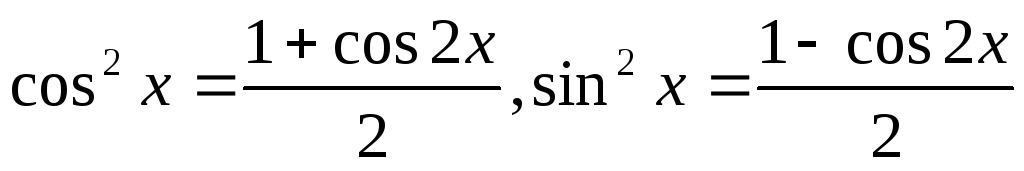10. Выражение синуса и косинуса через тангенс угла: , .

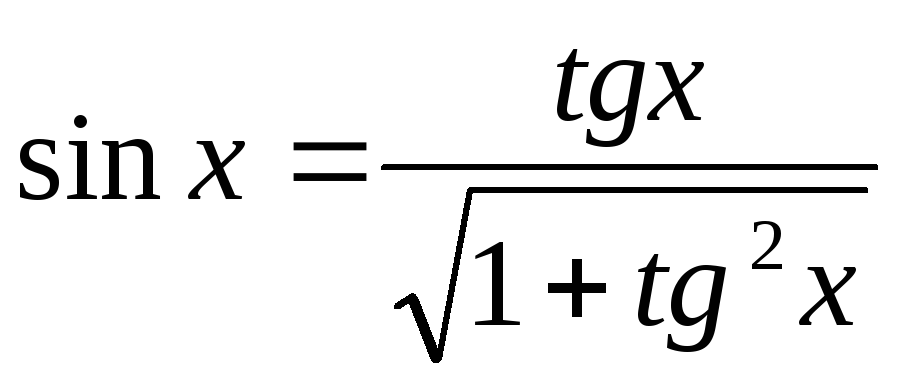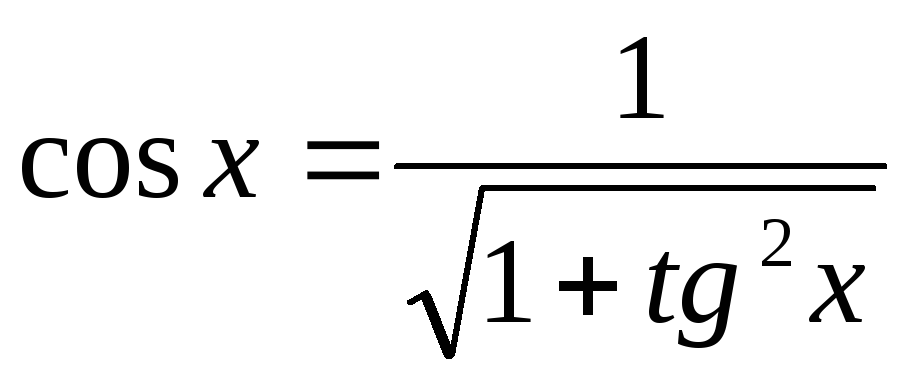11. Выражение синуса и косинуса через тангенс половинного угла: .

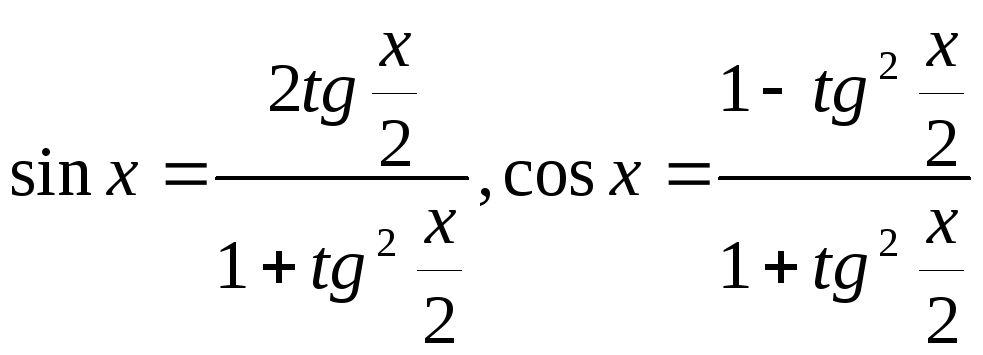Формулы преобразования суммы или разности в произведение

12. Сумма синусов: .

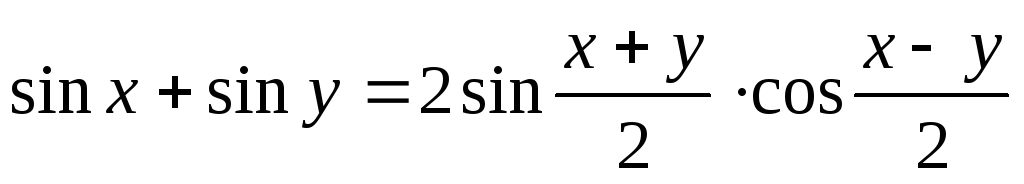13. Разность синусов: .

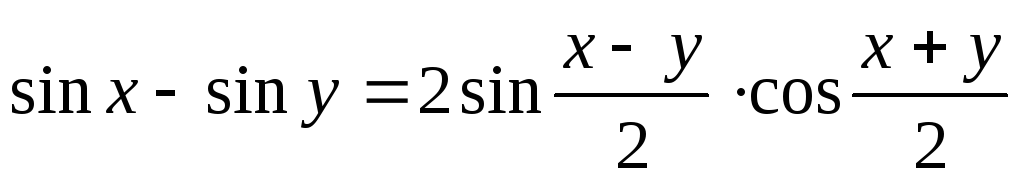14. Сумма косинусов: .

15. Разность косинусов: .

Формулы преобразования произведения в сумму или разность

16. Произведение синуса на косинус: .

17. Произведение синуса на синус: .

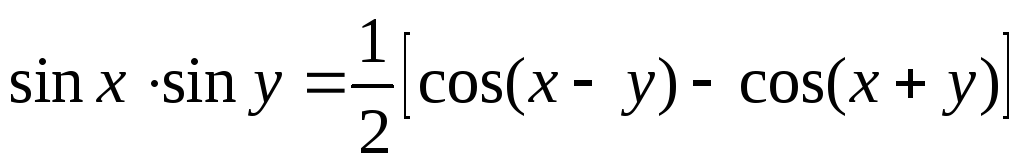18. Произведение косинуса на косинус: .

Таблица значений тригонометрических функций

	0
	0				1	0	-1	0
	1				0	-1	0	1
	0		1		-	0	-	0
	-		1		0	-	0	-

Прогрессии

1. Формула - го члена арифметической прогрессии

Здесь - первый член арифметической прогрессии, - разность прогрессии.

2. Формула суммы первых 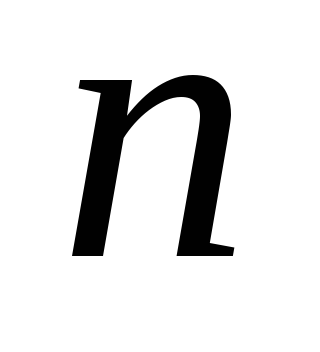членов арифметической прогрессии

3. Формула 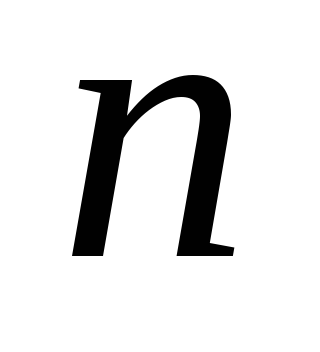- го члена геометрической прогрессии

Здесь - первый член геометрической прогрессии, - знаменатель прогрессии.

4. Формула суммы первых членов геометрической прогрессии

5. Формула суммы бесконечно убывающей геометрической прогрессии

Свойства гиперболических функций

1. , 2. ,

3. , 4. ,

5. ,

Формулы приведения

1. , 2.,

3. , 4. ,

5. , 6. ,

7. , 8. ,

9. , 10. ,

11. , 12. ,

13. , 14.

15. 16.

Таблица производных

1. , 2. ,

3. , 4. ,

5. , 6. ,

7. , 8. ,

9. , 10. ,

11. , 12. ,

13. , 14. ,

15. , 16. ,

17. ,

18. , ,

19. , ,

20. , ,

21. , .

Таблица интегралов

1. 2.

3. , 4. ,

5. 6. ,

7. , 8. . ,

9. , 10. ,

11. , 12.. ,

13. , 14. ,

15. , 16. ,

17. , 18. ,

19. , 20. ,

21. ,

22. ,

23. ,

24. , 25. ,

26. , 27. .

28. , 29. ,

30. ,

31. ,

Замечания.

1. Если то

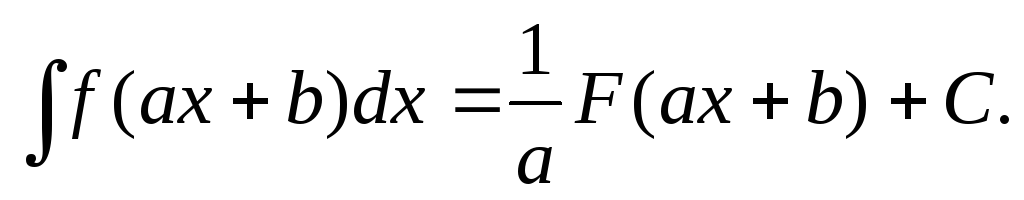
2. Рекуррентная формула для нахождения интеграла

, ,