
- •3 Звіт про проходження педагогічної практики
- •2. Активна практика
- •Тема уроку: ”Неперервність складеної функції. Неперервність елементарних функцій. Точки розриву та асимптоти”
- •Неперервність складеної функції. Неперервність елементарних функцій
- •Неперервність показникової функції
- •Неперервність логарифмічної функції
- •Неперервність обернених тригонометричних функцій
- •Неперервність степеневої функції
- •Похилі та горизонтальні асимптоти кривої
- •16 Тема уроку: ” Теорема обернена до теореми Піфагора”
- •17 Тема уроку: ” Розв’язання задач з похідними”
16 Тема уроку: ” Теорема обернена до теореми Піфагора”
Тип уроку: Урок вивчення нового матеріалу.
Мета: 1. Ознайомити учнів з теоремою оберненою до теореми Піфагора.
2. Сприяти формуванню в учнів уміння розв’язувати задачі пов’язані з теоремою оберненою до теореми Піфагора.
Вивчення нового матеріалу.
Теорема: (обернена до теореми Піфагора)
Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, то трикутник прямокутний.
Доведення:
Нехай у трикутнику ![]() :
:![]() .
Доведемо, що кут
.
Доведемо, що кут ![]() прямий. Побудуємо прямокутний
прямий. Побудуємо прямокутний ![]() з катетами
з катетами ![]() і
і ![]() .
За теоремою Піфагора
.
За теоремою Піфагора ![]() і отже,
і отже, ![]() .
Але за умовою теореми
.
Але за умовою теореми ![]() .
Тоді
.
Тоді ![]() або
або ![]() .
Отже трикутники
.
Отже трикутники ![]() і
і
![]() рівні за трьома сторонами. З рівності
трикутників випливає, що кут
рівні за трьома сторонами. З рівності
трикутників випливає, що кут ![]() трикутника
трикутника ![]() - прямий.
- прямий.
щ.п.б.д.
За доведеною теоремою, трикутники із сторонами 3, 4, 5; 5, 12, 13; 8, 15, 17; 7, 24,25 – прямокутні. Прямокутні трикутники, сторони яких виражаються цілими числами, називаються піфагоровими трикутниками.
Землеміри Стародавнього Єгипту для побудови прямого кута використовували такий спосіб: мотузку ділили вузлами на 12 рівних частин і кінці зв’язували. Потім мотузку натягували на землі за допомогою кілків так, щоб дістати трикутник із сторонами 3, 4 і 5. Тоді кут між сторонами 3 і 4 був прямий. Трикутник із сторонами 3, 4 і 5 часто називають єгипетським.
Завдання для домашнього опрацювання:
Вивчити конспект.
17 Тема уроку: ” Розв’язання задач з похідними”
Тип уроку: Урок вивчення нового матеріалу.
Мета: 1. Ознайомити учнів з поняттям похідної.
2. Сприяти формуванню в учнів уміння розв’язувати задачі з похідними.
Вивчення нового матеріалу.
Приклад
1. Знайти
похідну функції в точці ![]()
а)![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ;
;
г) ![]() ,
,
![]() .
.
Розв’язок:
а) за формулою обрахунку похідної: ![]()
б) аналогічно:
 в)
в) ![]()
![]() =|
=|![]() ,
коли
,
коли ![]() |=
=
|=
=![]()
Отже, ![]()
г) ![]() =|
=|![]() ,
коли
,
коли![]() |=
|=
=![]()
18
Приклад
2. Знайти
похідну функції
![]() в точці: а)
в точці: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
Відповідь:
а)4; б)10; в)-6; г) ![]() ..
..
Отже проглядається
закономірність: для кожної точки ![]() похідна буде
похідна буде ![]() ,
тобто
,
тобто ![]() .
.
Доведемо в загальному випадку:
![]() ,
,
отже похідна функції ![]() це теж функція, яка діє за формулою
це теж функція, яка діє за формулою ![]() .
.
Приклад
3. Знайти
похідну функції
![]() .
.
Розв’язок:
![]() .
.
Приклад
4. Знайти
формулу похідної функції
![]() .
.
Розв’язок: ![]() ,
отже
,
отже ![]()
Приклад
5. Знайти
формулу похідної функції
![]() .
.
Розв’язок:
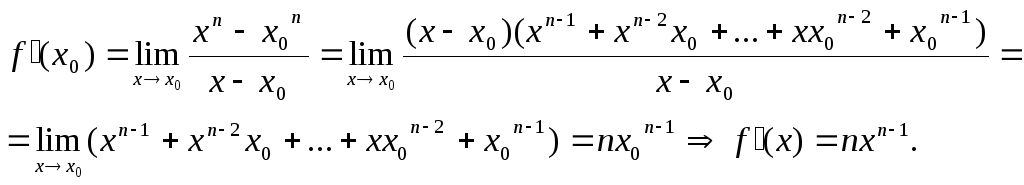
Приклад
6. Знайти
формулу похідної функції
![]() .
.
19
Розв’язок: 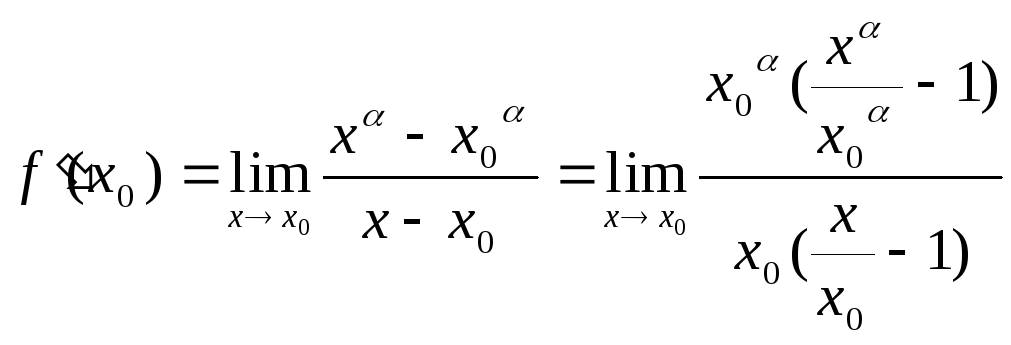 =|
=|![]() ,
,
коли
![]() |=
|=![]() ,
але звідси ми не можемо зробити висновок,
що
,
але звідси ми не можемо зробити висновок,
що
![]() , оскільки це буде не правильно для
, оскільки це буде не правильно для
![]() .
.
Перевіримо окремо:
Для
![]() :
:
![]() ;
;
Для
![]() :
:
![]() ;
;
Для
![]() :
:
![]() .
.
Отже
![]() ,
,
![]() не має похідної в точці
не має похідної в точці
![]() .
.
Висновок:
1) Для будь-якого![]()
2) Якщо
![]() визначена при
визначена при
![]() то
то
![]()
3) Якщо
![]() визначена на
визначена на
![]() і
і
![]() то
то
![]() при
при
![]()
4) Для будь-якого
![]() .
.
Приклад
7. Знайти
формулу похідної функції
![]() .
.
Розв’язок:
![]() .
.
Приклад
8. Знайти
формулу похідної функції
![]() .
.
Розв’язок:
![]() =
=
=|![]() ,
коли
,
коли
![]() |=
|=![]()
отже
![]() .
.
Зокрема
![]() .
.
20
Приклад 9. Знайти формулу похідної функції
![]() .
.
Розв’язок:
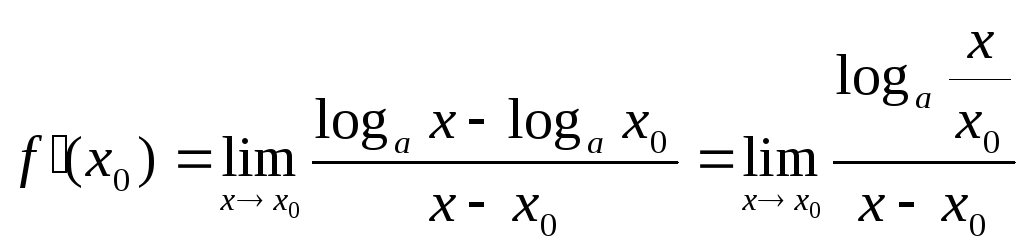 =
=
=|![]() ,
коли
,
коли
![]() |==
|==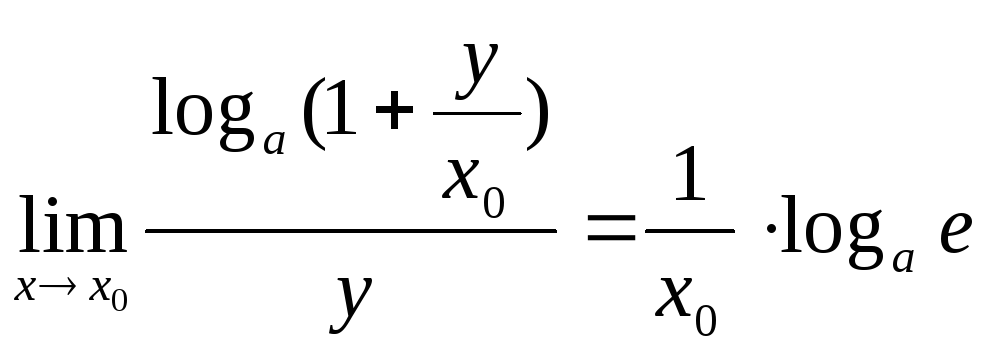 .
.
Отже
![]() ,
,
![]() ,
зокрема
,
зокрема![]() ,
,
![]() .
.
Приклад 10. Знайти формули для похідних функцій:
а)
![]() ,
б)
,
б)![]() ,
в)
,
в)
![]() tg
tg![]() ,
г)
,
г)
![]() ctg
ctg![]() .
.
Розв’язок: а)
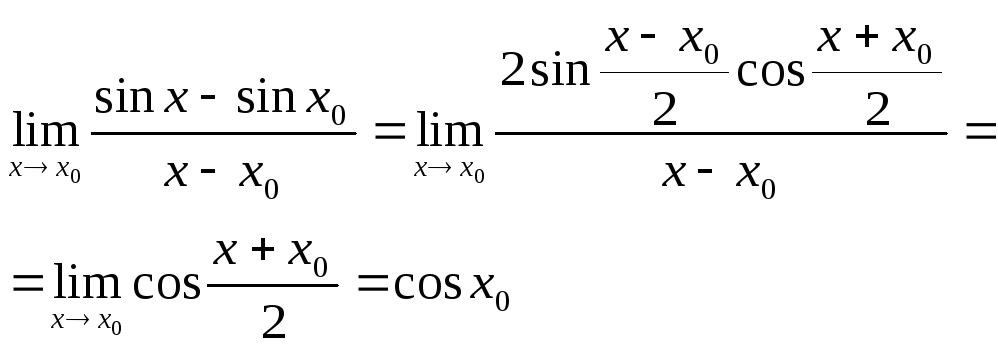
Отже
![]() .
.
б)
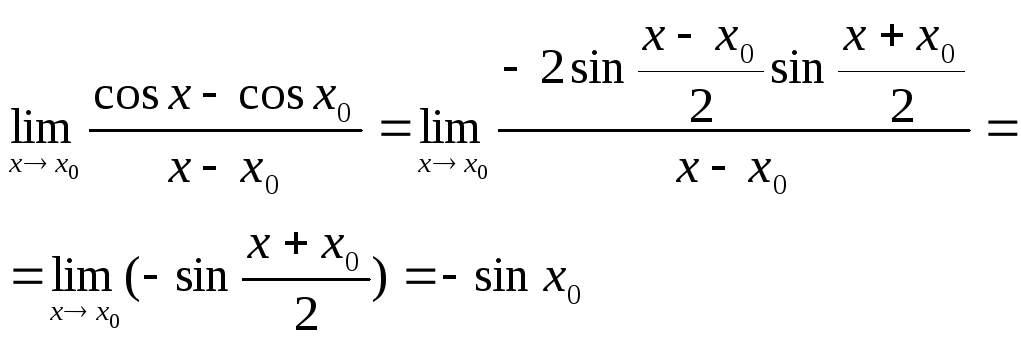
Отже
![]() .
.
в) (tg![]() )’=
)’=
![]() .
.
г) аналогічно пункту в):
(сtg![]() )’=
)’=![]() .
.
21
Завдання для домашнього опрацювання:
Вивчити конспект.
Зробити табличку похідних і вивчити її.
Знайти похідну функції
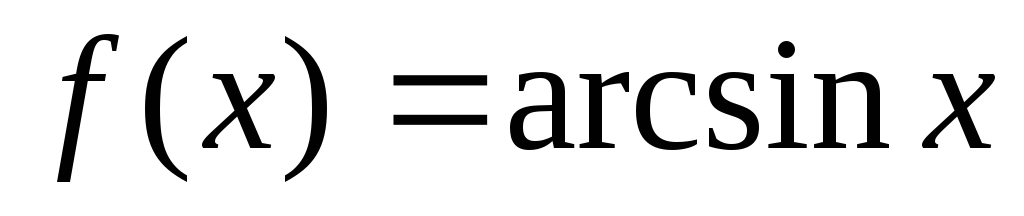 ,
,
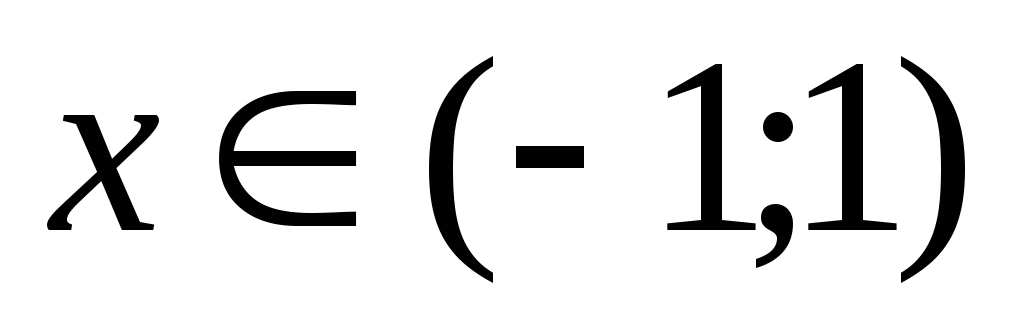 .
.
22
