Щоденник

педагогічної практики

спеціаліста

механіко-математичного факультету

Київського Національного університету

імені Тараса Шевченка

ПІБ

за період з 15 лютого по 13 березня 2010 р.

місце практики – КПНЛ №145

керівник практики – Басов Дмитро Сергійович

Київ 2010

Дата	Зміст роботи
9.02.2009	Ознайомлення з ліцеєм. Розмова з вчителем про навчальні плани	Виконано
11.02.2009	Відвідання уроку з геометрії студента практиканта Іваніщева К. Є.	Виконано
11.02.2009	Проведення залікового уроку з геометрії у 8-А класі	Виконано
12.02.2009	Відвідання уроку з геометрії у 10-А класі вчителя Басова Д. С.	Виконано
14.02.2009	Відвідання уроку з алгебри у 8-А класі	Виконано
16.02.2009	Проведення залікового уроку з алгебри в 10-А класі	Виконано
17.02.2009	Відвідання бібліотеки, підготовка до гри „Математична карусель”	Виконано
18.02.2009	Проведення гри „Математична карусель” між 10-Б, 10-В, 10-Г	Виконано
20.02.2009	Відвідання уроку з алгебри у 8-А класі	Виконано
21.02.2009	Відвідання уроку з геометрії студента практиканта Демчука К. В.	Виконано
23.02.2009	Відвідання бібліотеки, підготовка до проведення залікового уроку	Виконано
25.02.2009	Проведення залікового уроку з геометрії у 8-А класі	Виконано
28.02.2009	Відвідання уроку з алгебри в 10-А класі	Виконано
2.03.2009	Проведення уроку з алгебри в 10-А класі	Виконано
5.03.2009	Підведення підсумків практики	Виконано

3 Звіт про проходження педагогічної практики

Я, ПІБ, студентка механіко-математичного факультету Київського Національного університету ім.. Т. Шевченка проходила педагогічну практику з 9 лютого по 6 березня 2009 р. в КПНЛ №145.

Керівник практики від ліцею-вчитель математики Басов Дмитро Сергійович.

За період практики мною було виконано наступні види робіт:

1. пасивна практика

№	Тема уроку, лекції чи семінарського заняття, на якому був присутній практикант	ПІП викладача, або іншого студента практиканта, які проводили заняття	Навч. заклад, клас, група	Дата	Підпис викладача- методиста
1	„Пряма Ейлера”	Іваніщев К. Є.	8-А	11.02.09
2	„Площа проекції многокутника”	Басов Д. С.	10-А	12.02.09
3	„Неповні квадратні рівняння. Їх розв’язання”	Басов Д. С.	8-А	14.02.09
4	„Теорема Вієта.Теорема обернена до теореми Вієта”	Басов Д. С.	10-А	20.02.09
5	„Піраміда з рівно нахиленими до основи ребрами. Піраміда з рівно нахиленими до основи гранями”	Демчук К. В.	10-А	21.02.09
6	„Означення похідної. ЇЇ геометричний зміст”	Басов Д. С.	10-А	28.02.09

4

2. Активна практика

№	Тема уроку, лекції чи семінарського заняття	Навч. заклад, клас	Дата	Оцінка	Підпис викладача
1	„Коло дев’яти точок”	8-А клас	11.02.09
2	„Неперервність складеної функції. Неперервність елементарних функцій. Точки розриву та асимптоти”	10-А клас	16.02.09
3	„Математична карусель”	10-Б, 10-В, 10-Г	18.02.09
4	„Теорема обернена до теореми Піфагора”	8-А клас	25.02.09
5	„Розв’язання задач з похідними”	10-А клас	02.03.09

______________\ПІБ\

Вчитель математики ______________\Басов Д.С.\

Директор школи ______________\Левтік М. М.\

5

Відгук-характеристика

про проходження педагогічної практики

студенткою V курсу механіко-математичного факультету

Київського Національного університету імені Тараса Шевченка

ПІБ

Студентка ПІБ проходила педагогічну практику в КПНЛ №145 з 9 лютого по 6 березня 2009 року. За цей період вона відвідала чотири уроки вчителя математики та два уроки студентів практикантів, самостійно провела два уроки алгебри в 10-А класі та два уроки геометрії в 8-А класі. Разом з іншими студентами практикантами ПІБ підготувала і провела позакласний захід - „Математична карусель” між учнями десятих класів.

ПІБ старанно готувалася до уроків, працювала з різною літературою, слідкувала за порядком під час уроків, проводила педагогічну роботу по оформленню, проводила залікові заняття, а також перевірку самостійних та контрольних робіт учнів з виставленням оцінок.

Оцінка за навчальну роботу – „ ”.

Оцінка за виховну роботу - „ ”.

Директор школи ___________ \Левтік М. М.\

Вчитель математики ___________ \Басов Д. С.\

6

Рецензія

на відвіданий урок, проведений 20.02.09 в 10 класі КПНЛ №145 на тему „Теорема Вієта. Теорема обернена до теореми Вієта”

...

Рецензент __________ студентка-практикантка ПІБ

7

ПЛАНИ-КОСПЕКТИ ПРОВЕДЕНИХ ЗАНЯТЬ

Тема уроку: ”Коло дев’яти точок”

Тип уроку: Урок вивчення нового матеріалу.

Мета: 1. Ознайомити учнів з ГМТ: коло дев’яти точок.

2. Дати означення кола дев’яти точок.

3. Сприяти формуванню в учнів уміння використовувати коло дев’яти точок, для розв’язання задач.

Вивчення нового матеріалу.

У будь-якому трикутнику можна провести коло через такі три трійки точок (рис.1): основи його висот K,M іN, основи його медіанD, E і F, серединиO, P і Q відрізків, що сполучають ортоцентр трикутника з його вершинами. Це коло знайшов уXVIII ст. великий учений Л. Ейлер і називається воно колом Ейлера або числом точок – колом дев’яти точок.

Середини відрізків, що сполучають ортоцентр трикутника з його вершинами, називають точками Ейлера.

Рис.1

Д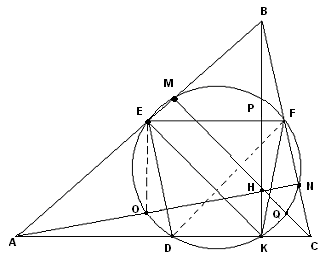оведемо, щосередини сторін трикутника, основи його висот і точки Ейлера лежать на одному колі.

Доведення: Нехай D, E, F – середини сторін трикутника ABC (Рис. 1); K, M, N – основи його висот; O, P, Q – точки Ейлера; H – ортоцентр.

Проведемо через точки D, E, F коло. Доведемо, що точки K і O лежать на цьому колі. Чотирикутник DEFK – трапеція, оскільки EF||AC (EF – середня лінія трикутника ABC) і EF||DK. KE – медіана прямокутного трикутника ABK, проведена з вершини прямого кута, тому . ОскількиDF – середня лінія

8

трикутника ABC, то . ЗвідсиKE=DF. Отже, трапеція DEFK – рівнобічна., а тому коло, яке проходить через три її вершини D, E, F, пройде і через четверту вершину K.

Сполучимо точки O і F з точками E і D. Розглянемо чотирикутник DOEF. Пряма EO||BK(EO ABH) EF||AC, а тому . ОскількиDO||CM (DO – середня лінія трикутника AHC), а (за умовою), то. Враховуючи, щоDF||AB, дістанемо, тобто. Отже, навколо чотирикутникаDOEF можна описати коло. Таким чином, коло, яке проходить через три точки D, E і F, проходить через точки K і O.

Аналогічно доводимо, що коло пройде і через інші чотири точки M, P, N і Q.

Коло дев’яти точок можна побудувати, якщо знати дві його властивості.

1. Центр кола є серединою відрізка, який сполучає центр описаного навколо трикутника кола з ортоцентром трикутника.

2. Радіус кола дорівнює половині радіуса описаного навколо трикутника кола.

Завдання для домашнього опрацювання:

Вивчити конспект.

9